「軽い糸」に意味はあるの？糸の張力の大きさは両端でいつも同じ理由
軽い糸と質量のある棒の扱いの違いが分かる
軽い糸の張力の大きさが等しい理由がわかる
質量のある棒の張力の大きさが異なる理由が分かる
こんにちは。
よく問題文を見ると「軽い糸」というワードをよく見ます。
何となく流しているかと思うんですが、実はこのワードがあるかないかで問題の状況が大きく変わってしまいます。
結論からいうと「軽い糸」というワードがあることで
糸の張力の大きさが両端で等しくなる
ということが言えるんですね。
糸の張力の大きさが両端で等しくなるかどうかで問題の難易度が変わります。
今回は
なんで「軽い糸」だと糸の張力の大きさが両端で等しくなるのか。
そして、棒などの軽くない場合でつなぐとどうなるのか
これらを説明していきたいと思います。
目次
糸の張力の大きさは両端で等しくなるの？
物体をつなぐ糸は99%「軽い糸」とみなします。
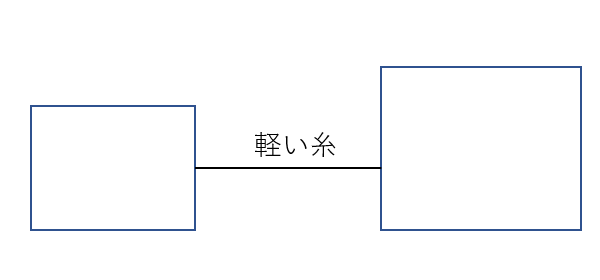
「軽い」というのは物理では「質量が０と考えて良い」と言い換えることができます。
このような状況で物体に働く力を書く時に、何も意識しないでこう書きますよね。
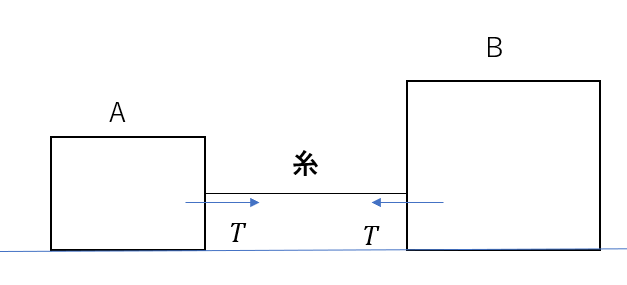
書きますね！
AIさん
物体A,Bがそれぞれ引き合う方向に同じ大きさ\(T\)で力が働く
と何も疑問を持たずに書きますよね？
もちろんこれは合ってます
でも、なぜ張力の大きさが等しいと言えるんでしょうか？
そう言われると・・・
リケジョを目指すAIさん
質量のある棒の張力の大きさは等しくなる？
もう一つこんな状況も考えてみましょう。
先ほどの物体A,Bが質量\(w\)の棒でつながれている。
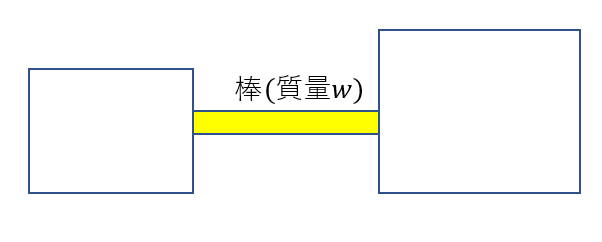
同じように書く物体に働く棒の張力（棒から受ける力）を書いてみてください。
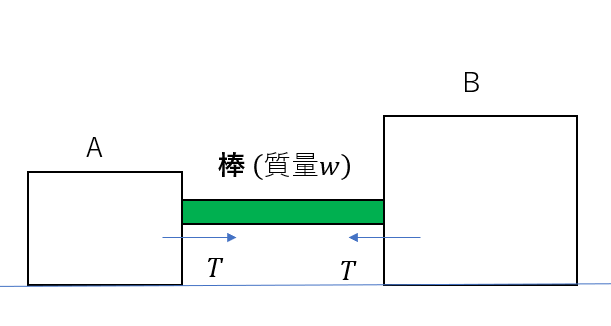
はい書けました。さっきと同じですね。
リケジョを目指すAIさん
と、やってはダメですよ！
あっきー
さっきのように、張力の大きさは両端で等しくなる・・・
のではありません！
大きさがしっかり異なってます。
この2つの例を見ると、一つ違いがありますね。
質量があるかないか
です。
これを元に運動方程式を考えるとすべて解決できます！
「軽い糸」なら糸の張力の大きさは等しくなる
先ほどの糸の例を見てみましょう。
今までは物体について運動方程式を立てていますが、今回は糸について運動方程式を立てます。
\(m\vec{a} = \vec{F}\)
最初にも言いましたが「軽い」というのは「質量を0と考えて良い」という意味です。
なので運動方程式に\(m=0\)を代入すると
\(\vec{F} = 0\)
となります。
さて、運動方程式の記事でも説明をしましたが。
\(\vec{F}\)っていうのはただの「力」ではなく、合力です。
「糸には力が働いていない」という意味ではなく。
「糸にはたらいている力を足し合わせたら０になる」ということを表しているんですね。
つまり力がつり合っているということです。
そこで、糸にはたらく力を書きだしてみるとこうなります。
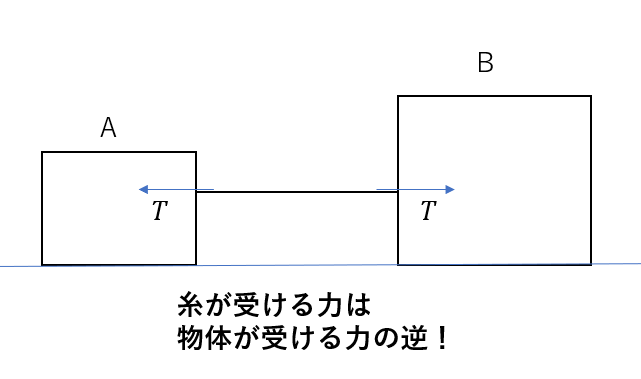
ここは注してほしいのですが、最初に見せた力は物体が受ける力です。
今回は糸が受ける力を考えないといけないので、このように向きが逆になります（作用反作用の法則）。
そして糸は力がつり合っている必要があるので、この両端の力は左右逆向きで力の大きさは同じなんです！
つまり、「軽い糸」であれば糸の両端の力の大きさは等しくなるのです！
なるほど！運動方程式から分かることだったんですね。
リケジョを目指すAIさん
質量がある棒は張力の大きさは等しくならない
一方で
質量\(w\)の棒の場合はどうなるでしょう？
全く同じように棒について運動方程式を立ててみましょう。
\(m\vec{a} = \vec{F}\)
んで、今回\(m=w\)ということなので
\(w\vec{a} =\vec{F}\)
となります。
加速度が生じているとすれば、左辺は０ではありませんね。
合力は0じゃないんです。
つまり、力はつり合っていないのです！！
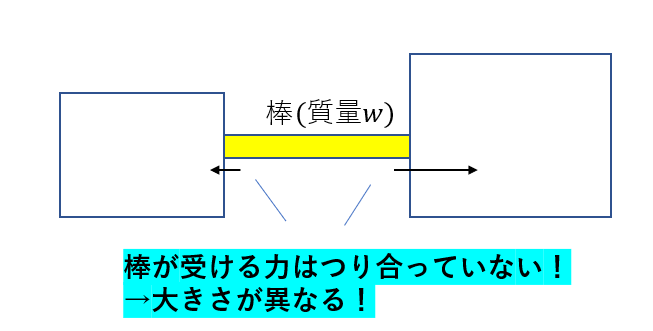
つり合っていないんだから、棒が受ける両端の力の大きさはもちろん異なります。
なので、各物体に働く力の大きさも違うんです。
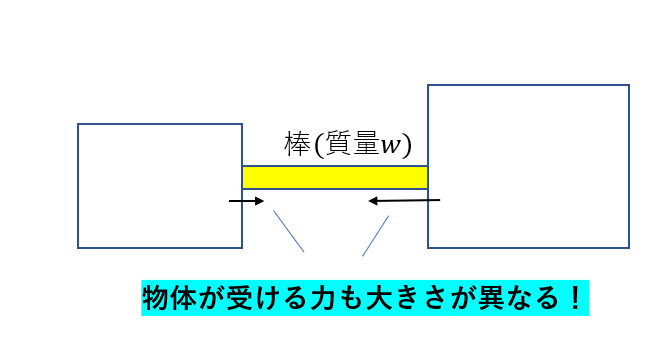
私、完全に引っかかった・・・なるほど、棒のように質量を無視できないときは注意しないといけないんですね。
リケジョを目指すAIさん
気づかずに入試本番になってしまうと大変です。ここで理解できて良かったですね！
あっきー
暗記ほど怖いものはない
いかがでしたか？
「糸だから常に張力が等しい」というように暗記するのは本当に怖いです。
糸は糸でも「質量のある糸」であれば張力は等しくなりません。
「なぜ？」と思ったときに「こういうものだ」と暗記するのではなくしっかり式で説明できるようにしてください。
それが理解につながって、模試でも入試でも通用する知識になるのです。
もちろん暗記しなければいけないこともあります。
ですが、暗記しなくて良いものは極力暗記せず、導出したり説明できるようにしてください。
糸の張力の大きさは常に等しいわけではない
→運動方程式から理解しよう
オンライン物理塾長あっきーからのお知らせ！
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます！今ならすごいサポート特典もあります！
＊無料の物理攻略合宿よりも充実のコンテンツです！
Comment
運動方程式のFが合力であることはこんなところにも生きてくるんですね。
糸の質量を無視すると張力が等しくなるということ自体は、縦に二物体を糸でつないだとき「糸の分も下向きに力が働いてしまって張力が等しくならない」とかいう言い方で説明されましたが横向きに並べたときというのは盲点でした。
運動方程式の意味は雰囲気の違う感じ?でいろんなところに出てくるので毎度驚かされます…。
すばらしい発見ができたようでうれしいです。