【物理基礎】等加速度直線運動の3公式の覚え方と使い方とは?

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
等加速度運動の公式は物理基礎で習う最初の公式だと思います。
最初なだけあって簡単ですが、9割の高校生が間違った覚え方をしています。
おかげさまで、自由落下、斜方投射・・・などの落下運動の種類で公式を分けるという完全アウトは覚え方をしてしまうのです。
この記事では、等加速度運動の公式を正しい覚え方とその使い方について学んでいきましょう。
最後まで読めば、落下運動を種類別に公式を覚える必要がなくなります!
目次
等加速度直線運動とは?
等加速度運動とは一定の加速度で運動することです。

一定の加速度というのは、時間的に向きも大きさも一定ということです。
等加速度運動が起こるには物体にはたらく合力が一定である必要があります。
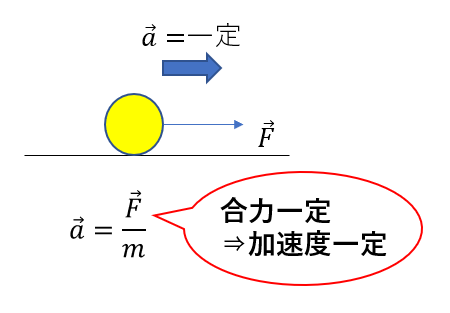
運動方程式より\(\vec{F}\)が一定であれば\(\vec{a} = 一定\)となりますね。
運動方程式に関してはこちらの記事で詳しく説明しています。
等加速度直線運動の公式を導出する前に知っておくべきこと

等加速度運動の公式を導く前に次のことを頭に入れておいてほしいです。
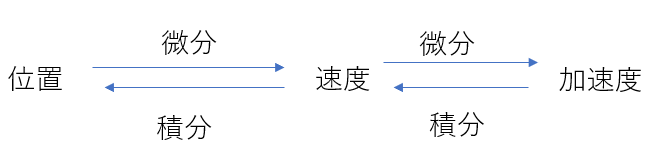
時間\(t\)で、位置\(x\)を微分すれは速度\(v\)になり、速度を微分すれば加速度\(a\)になります。
逆に加速度を積分すれば速度に、速度を積分すれば位置になります。
そして、微分と積分のグラフ上の意味についても理解しておきましょう。
- 微分=接線の傾き
- 積分=面積
微分積分を習っていない人は次のように理解しておきましょう。
グラフの接線の傾きを求めると、位置→速度→加速度と求められる。
グラフの面積を求めると、加速度→速度→位置と求められる。
等加速度直線運動の公式の導出

では、等加速度直線運動の公式を導出していきます。
物体が一定の大きさ\(a\)で右向きの加速度を生じながら直線運動している。時刻\(t = 0\)で、物体は初期位置\(x_0\)にあり、速さ\(v_0\)で右向きに動いているとき、時刻\(t\)での物体の速さ、および位置を式に表せ。

等加速度運動の公式導出1:加速度の面積を求める
先ほどの関係を見てください。
加速度を積分、つまりグラフの面積を求めることで速度を出すことができます。
なので、加速度と時間のグラフが書ければ速度(速さ)は求められます。
今回、加速度は一定なので、加速度と時間のグラフはこんな感じになります。
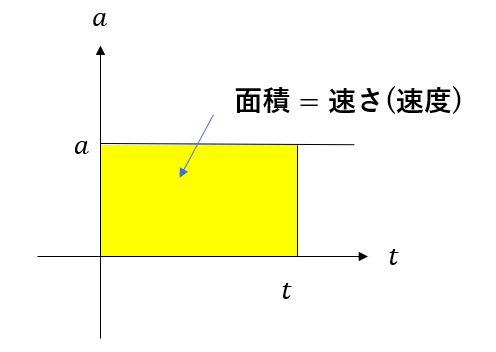
この図形は長方形なので面積を求めるのは簡単ですね。「縦×横」です。
縦が\(a\)、横が\(t\)なので
面積=\(at\)
と表せます。
しかしこのままでは、\(t=0\)のときに、速度が0になってしまいます。

なので、\(v_0\)を足してあげます。
\(v =v_0 + at\)
このようにすれば、\(t = 0\)のとき\(v = v_0\)となりますね。
これで速さが求まりました。
等加速度運動の公式導出2:速度のグラフの面積を求める
今度は位置を求めていきます。
先ほどと同じように、今度は速さのグラフの面積を求めればOKです。
先ほど求めた\(v\)の式から、グラフを書いてみます。
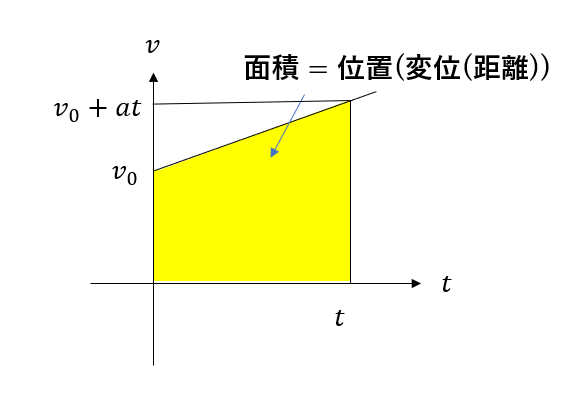
\(t\)の1次関数なので直線になりますね。
今回は台形ですが、求められますね。
面積=\(v_0t + \frac{1}{2}at^2\)
これが位置になるわけですが、\(t=0\)とすると、初期位置が原点になります。

なので、\(x_0\)を足してあげましょう。
\(x=x_0+v_0t + \frac{1}{2}at^2\)
これでOKですね。
この\(x\)は位置の式です。教科書では「変位」の式として紹介されています。
変位\(\Delta x = x – x_0\)です。なのでこの位置の式は
\(\Delta x = v_0t+\frac{1}{2}at^2\)
変位の式に置き換えることができます。こちらが一般的なので今後はこれをを使っていきます(今後は\(\Delta x\)を\(x\)と表記)。
高校生の9割が知らない等加速度運動の真の公式

ここまでは教科書通りですね。
しかし、今出した式は本当の公式ではありません。
このまま覚えると挫折します。
今の状況は、初速度が右向きで加速度も右向きの場合しか考えていません。
実際は、いろんな状況が考えられますよね。
初速度が左で、加速度が右、
初速度が左で、加速度も左
それぞれの状況で式を場合分けするのは使い勝手が悪すぎますね。
なので、場合分けしないで良い本当の等加速度運動の公式を教えます。それがこちら。
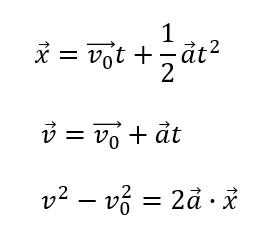
ポイントはベクトルの関係式であるということです。
ですから、ベクトルを扱った計算をする必要があります。これについては後程お話しますね。
この等加速度運動の公式の注意点を2つお伝えします。
等加速度直線運動の公式注意1:\(\vec{x}\)は変位
まず、式に出てくる\(\vec{x}\)の式は「変位」です。
変位は「位置の変化量」です(この大きさが移動距離です)。
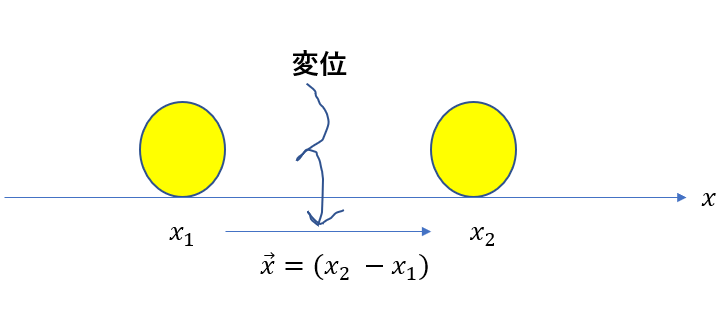
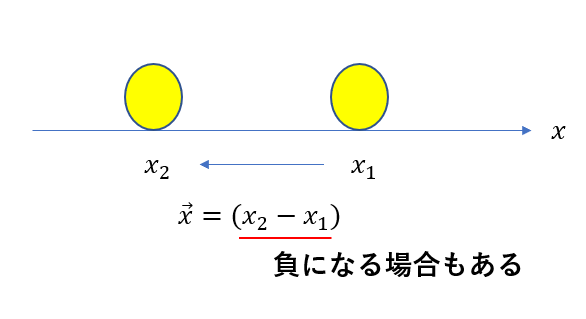
変化量は「後-前」で計算されます。
なので場合によってはマイナスになることもあります。マイナスになろうと「後-前」です。
等加速度直線運動の公式注意2:\(\vec{a}・\vec{x}\)は内積
もう一つ、3つ目の式の右辺にある\(\vec{a}・\vec{x}\)は内積と呼ばれるものです。
要は掛け算です。
ベクトルの成分を掛け算すればOKです。
等加速度直線運動の公式の使い方

では、実際に公式の使い方を見ていきます。
ここで必要なのはベクトルの扱い方です。
- 軸を取る
- 軸に沿ってベクトル成分を決める
- 式に代入する
重要なポイントはこれです。ベクトルについて詳しく学びたい人はこちらの記事をご覧ください。
図のように、角度\(\theta\)をなす斜面の下端から斜面上向きに大きさ\(v_0\)で打ち出す。下端の位置を原点に取り、斜面上向きに軸を取ったとき、時刻\(t\)における速度\(\vec{v}\)と位置\(\vec{x}\)を求めよ。ただし重力加速度の大きさを\(g\)とする。
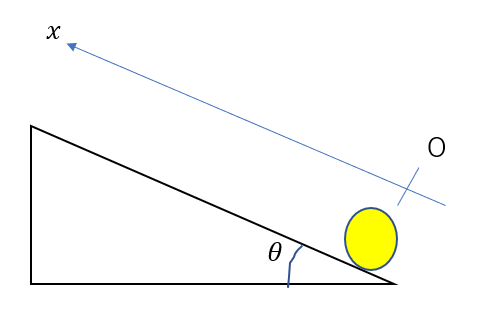
等加速度直線運動の公式使い方1:軸を取る
まず、軸を取ります。
これは問題で設定されていますね。斜面上向きに取ります。
等加速度直線運動の公式使い方2:ベクトルの成分を書く
次にベクトルの成分を書いていきます。
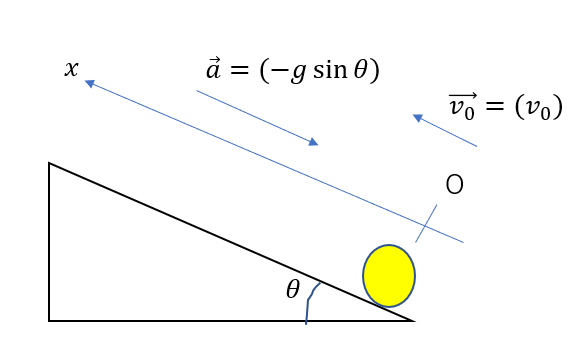
初速度は大きさが\(v_0\)で向きは軸と一致しているのでこのままでOKです。
加速度は大きさが\(g\sin{\theta}\)で向きが軸と逆向きなので、負になります。
等加速度直線運動の公式使い方3:式に成分を代入
先ほど求めたベクトルの成分(図のカッコの中身)を公式に代入します。
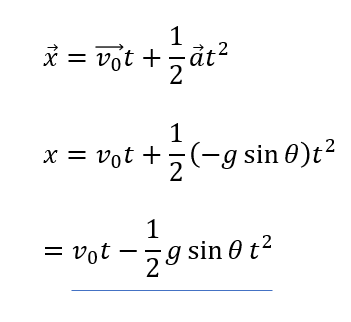
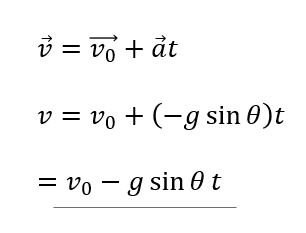
これで求めることができます。
この手順を踏んでいけば、マイナスとかは自然に現れます。
まとめ:等加速度直線運動の公式はベクトルの式
いかがでしたか?
等加速度直線運動の公式はこのようにベクトルの式で表せるんです。
ここを知っておくと、覚える公式の数も減りますし、符号ミスなども減ります。
しっかり復習して問題を解きましょう。
等加速度運動の公式
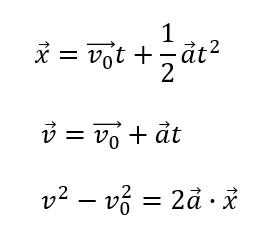
*この3だけ覚えるべし。パターン化しなくて良い。
*計算するときはベクトルの扱いに注意すること
・軸を取る
・ベクトルを成分表示して、成分を代入
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!