ダイオードの性質とは?ダイオードの回路問題の解き方を徹底解説
どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
ダイオードの問題が模試で出てきたんですが、授業でやったことなくて全滅しました。。。ダイオードの問題はどうすれば解けますか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
ダイオードの回路問題が初見で出てきて無事全滅。。。そんな経験ありませんか?
ダイオードの回路問題を学校でやっていればいいんですが、初見だとイタイ目に合います。
ですが、ダイオードの問題の解き方はワンパターンです。ダイオードの性質さえ理解してしまえば楽勝です。
この記事では、ダイオードの性質を分かりやすく解説し、入試問題に触れていきます。
最後まで読むことで、ダイオードを含む回路問題を楽々解けるようになります。また回路問題の重要なポイントも理解できるので点数アップにつながりますよ。
ダイオードの性質が理解できる
ダイオードの入試レベルの問題が解ける
回路問題の解き方が分かる
目次
ダイオードの性質とは?

ダイオードはめちゃめちゃ簡単に言えば
特殊な抵抗
です。
電圧のかかり方で電流が流れるかが決まる

どのように特殊かと言うと、向きによって電流が流れなかったり流れたりします。
ダイオードは回路図では以下のように書きます。
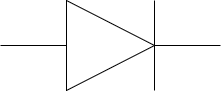
このとき、「左から右へ電流は流すが、右から左へは電流を流さない」というシステムになっているんです。
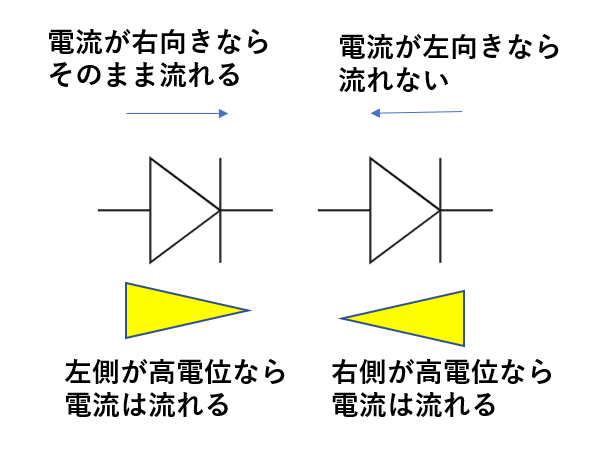
(電圧マークがダイオードの三角形と同じ形だったら電流は流れると覚えておくと忘れないですね。)
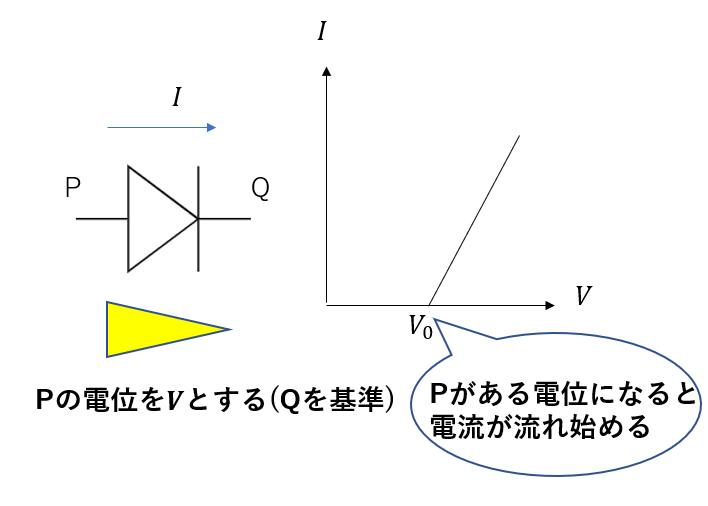
ただ、正確には左側が高電位でも電流がすぐ流れるわけでなく、図のようにある電圧以上の電圧がかかると電流が流れるようになります。
ダイオードはスイッチと抵抗に置き換えられる

このように、ダイオードは特殊な抵抗なのです。
ですから、ダイオードは普通の抵抗に置き換えることができます。
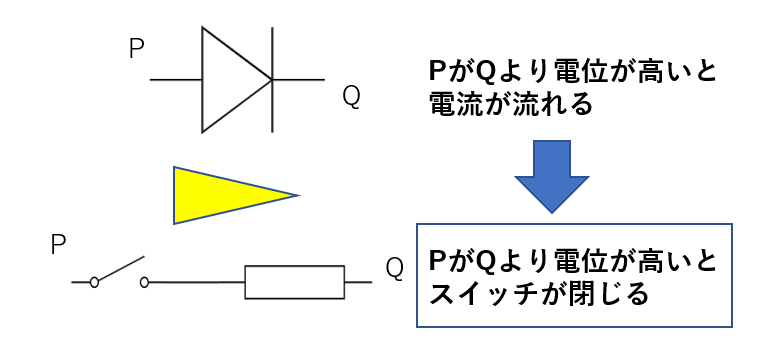
電流が流れるかどうかはスイッチの開閉で考えれば、このようにスイッチと普通の抵抗でダイオードは表すことができます。
もちろん問題によって電位差が\(V_0\)だけ大きくなった時に電流が流れるなど、条件は変わってきます。あくまでイメージです。
当然、抵抗なので電圧降下も起こります。キルヒホッフの法則を考えるときはダイオードの電圧も考えなければいけません。
問題ではコンデンサーのように扱え!

ダイオードの問題ではあるとっておきの裏ワザがあります。
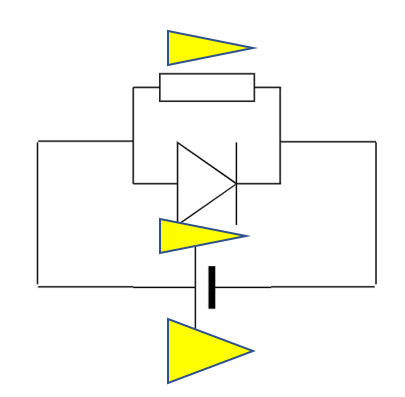
例えばこのような回路の場合、ダイオードには左側の電位が大きくなりますから電流は流れます。
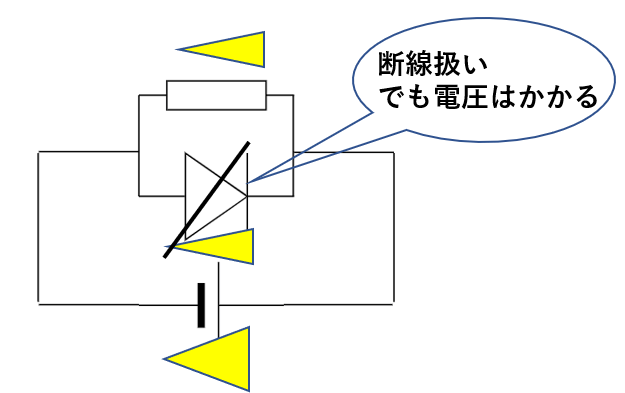
一方で電源の向きを逆にした、この回路ではダイオードには電流が流れません。
つまり断線扱いになります。
しかし、電圧はかかっています。
これって・・・コンデンサーと似てません?
これとそっくりですよね?
この扱い方を理解しておいてください。
コンデンサ―についてはこちらを確認してください
ダイオードを含む回路問題

ではこれを踏まえて、入試問題を解いてみましょう。今回はなんと、東大の問題です!
え?東大ですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
大丈夫。ここまでの話が理解できていれば十分解けるよ!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
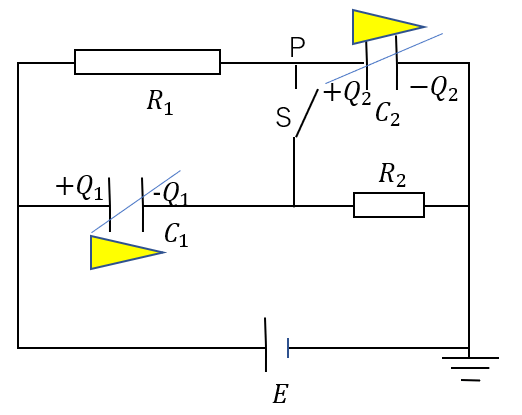
図のような回路がある。ダイオードD1はP1よりP0の方が電位が高いとき、D2はP2よりP1の方が電位が高いときに電流が流れる。電源の起電力はともに\(V_0\)であり、コンデンサーの電気容量はともに\(C\)とする。はじめ、スイッチはどちら側にも接続されておらず、コンデンサーには電荷が蓄えられていないものとする。点Gの電位を0,P1の電位を\(V_1\)、P2の電位を\(V_2\)としてとして以下の問いに答えよ
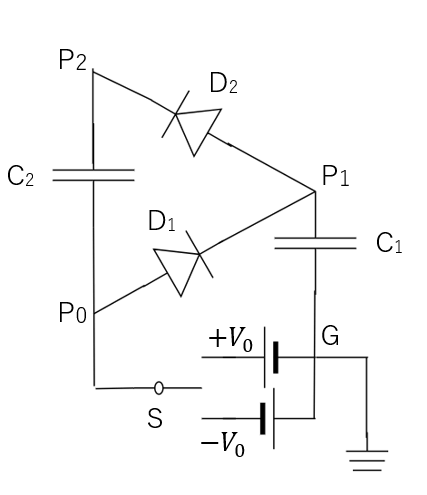
(1) スイッチSを\(+V_0\)側に接続した。その直後の\(V_1, V_2\)を答えよ。
(2) (1)のあと、回路中で電荷の移動がなくなったときの\(V_1, V_2\)を求めよ。またC1に蓄えられた静電エネルギー\(U\)、電池がした仕事\(W\)を求めよ
(3) (2)の後スイッチSを\(-V_0\)側に切り替えた。この直後の\(V_1, V_2\)を求めよ。
(4) (3)のあと、回路中で電荷の移動がなくなったときの\(V_1, V_2\)を求めよ。
(セミナー物理2019 問492)
回路問題のポイント

回路問題を解くポイントは2つです。
- 電圧マークを書く
- 「一周した電位=0」を使う
とにかくこれがすべてです。これにコンデンサーの性質だったりダイオードの性質をうまく利用して解いていきます。
これに関して詳しく知りたい方はこちらの記事を読んでください。
ダイオードの回路問題の解説
(1) スイッチを入れた直後→コンデンサーは導線扱い
(1)では「スイッチを入れた直後」というのがポイントになります。
スイッチを入れた直後ではコンデンサーには電荷が貯まっておらず、導線扱いになるのでした。
これを踏まえて電圧マークやダイオードについて情報を書き足していきます。
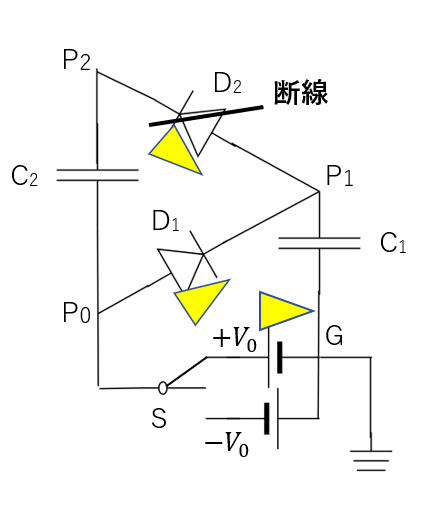
後は、回路をたどっていけば求めることができます。
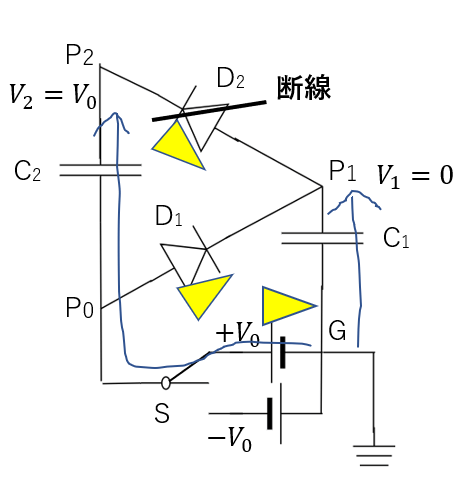
\(V_1 = 0, V_2 = V_0\)
これが答えです。
(2) 十分に時間が経過→コンデンサーは断線扱い
(2)では十分に時間が経過しています。つまりコンデンサーは断線扱いです。
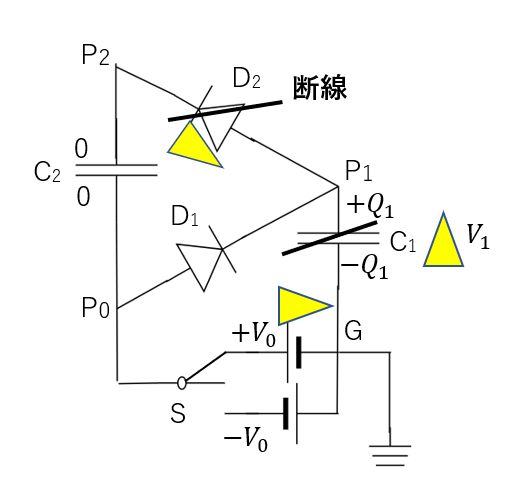
まず、ダイオードD2は(1)の時点で断線扱いなので、コンデンサーC2には電流は流れません。つまり、電荷が貯まることなくC2の電位差は0です。
ということで\(V_2 = V_0\)です。
また、C1にはコンデンサ―が蓄えられ断線扱いになります。すると、D1にも電流が流れなくなるのでD1の電位差は0になります。
ということで、「一周した電位=0」より
\(V_0 – V_1 = 0\)
∴\(V_1 = V_0\)
となります。
静電エネルギーは
\(U = \frac{1}{2}CV^2 =\frac{1}{2}CV_0^2\)
また、電池は電荷量\(Q = CV_0\)を電圧\(V_0\)で運んだので、電池のした仕事は
\(W = QV = CV_0^2\)
となります。
(3) スイッチを入れた直後→電荷の移動はない
(3)ではスイッチを入れた直後なので、電荷の移動が起こりません。つまり、コンデンサーの電荷は(2)と同じ状況になります。
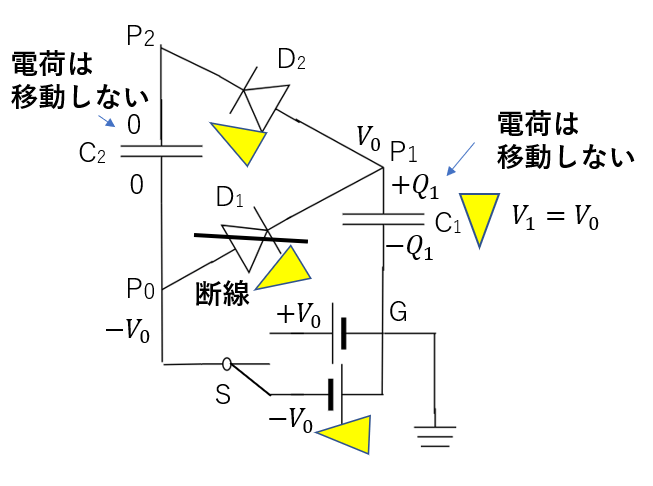
ダイオードは(3)においてはあまり関係ないので取りあえず無視します。
この状況で(1)と同じように点Gから回路をたどっていけば電位が求められます。
\(V_1 = V_0, V_2 = -V_0\)
が答えです。
(4) 島を見つけろ!
(4)で電荷の移動が始まります。ここで(3)の回路をもう一度見てみます。

先ほど触れなかったダイオードについて見ていきます。
まず、D1ですが、ここは明らかに断線扱いですね。P1の方がP0の電位よりも高くなるので。
逆にD2は図の通り電流が流れるようになります。
D1は断線して、D2には電流が流れる・・・
つまり電荷の移動が行われるのはこの部分ですよね?
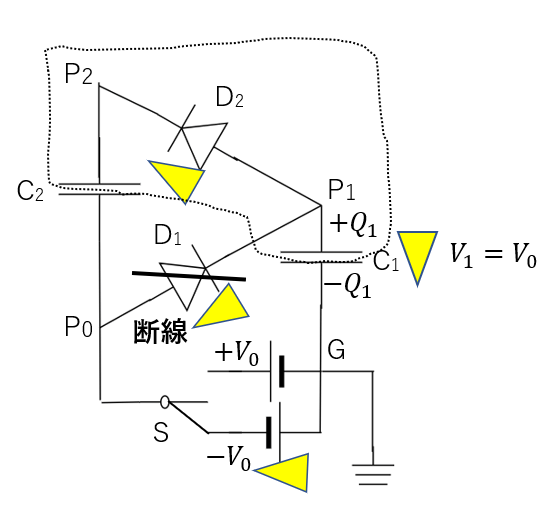
これは島になっているので電荷保存則が使えますね。
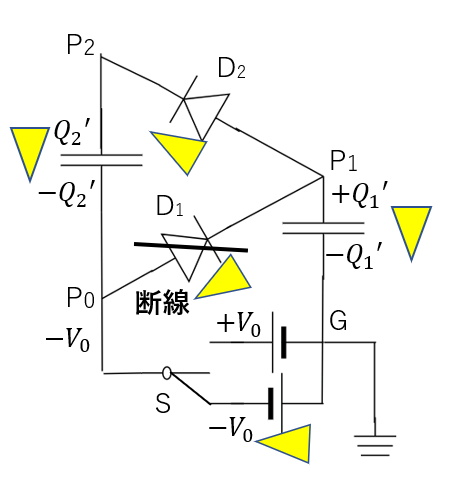
図のように電荷が分布されたとして、最初は\(Q_1 + 0 = CV_0\)の電荷が蓄えられていたので
\(Q_1′ + Q_2′ = CV_0\)
という関係が成り立ちます。
コンデンサ―C1からコンデンサ―C2に電荷が送られます。すると、P1の電位が小さくなり、P2の電位が大きくなります。
そしてP1とP2の電位が等しくなるとダイオードの電位差が0になりそれ以降電流が流れなくなります。
つまり、電荷の移動がなくなるとき、\(V_1 = V_2\)となります。
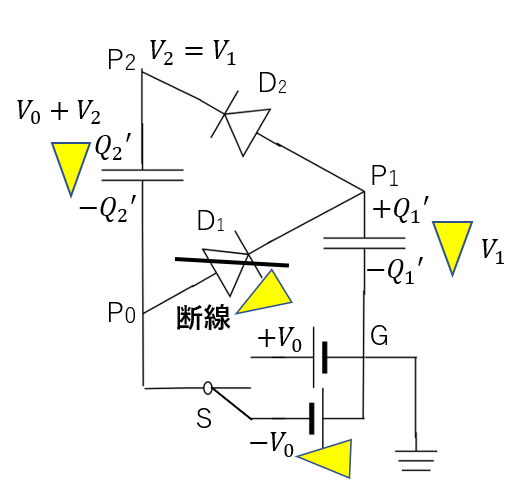
各電位差の大きさは図のようになるので
\(Q_1′ = CV_1, Q_2′ = C(V_0 + V_2) = C(V_0 + V_1)\)
後は先ほど電荷保存則から求めた式を使えば
\(CV_1 + C(V_0 + V_1) = CV_0\)
∴\(V_1 = 0\)
また
\(V_2 = V_1 = 0\)
となります。
これですべての問題が解けました。
意外と簡単に解けた!うれしい!!
 リケジョ志望のAIさん
リケジョ志望のAIさん
しっかり順を追ってみていけば回路問題が解けるので力を伸ばしていこうね
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
まとめ:状況をしっかり把握する

いかがでしかた?
ダイオードの扱い方が分かっていればただの回路問題なわけです。
- ダイオードにかかる電圧によって断線するかどうかが決まる
- 断線した場合でも電圧はかかる
これをしっかり理解しておきましょう。










Comment
電池のした仕事がどうしたらQEになるのかが分かりません。知恵袋は電圧かける電流でしたが重問はQEでした(Eは起電力)。
どうしたらこの式がでてくるのか、また、電池のした仕事の正体というかイメージを教えてください。よろしくお願いします。