円運動の問題の解き方【一周する条件を正確に考えてみた】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
円運動で出てくる「1周する条件」というのが分からないです…
 リケジョになりたいAIさん
リケジョになりたいAIさん
今回はこの悩みについて話したいと思います。
1周する条件は「糸がたるまない」や「面から離れない」などの説明がありますが、本当の条件はこのように表せます。
1周する条件
常に中心向きの力がはたらく
これが本当の条件です。これを理解することで、円運動の問題は解けるようになります。
円運動の問題を実際に解いて、確認してみよう!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
1周する条件が使いこなせる
円運動の問題が解けるようになる
目次
円運動の問題:「1周する条件」
図のように、質量\(m\)の物体に糸がつけられている。最下点から初速\(v_0\)を与えると円運動した。鉛直方向からの角度を\(\theta\)とする。ただし、\(\theta\)は反時計回りを正とし、重力加速度の大きさは\(g\)とする。また、円軌道の半径を\(r\)とする。
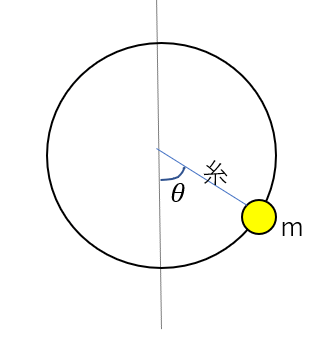
(1)角度\(\theta\)のときの物体の速さを求めよ
(2)角度\(\theta\)のときの糸の張力の大きさ\(T\)を\(v\)を用いて表せ。
(3)実際に物体が円運動し続けるには\(v_0\)に条件が必要である。その条件を求めよ。
まずは自力で解いてみましょう。
円運動のポイントはこちらの記事で解説しています。困ったらこちらの記事を見ながらでもいいので自分でまずは取り組んでみてください。
円運動の問題の解説
円運動の問題と来たら、この二つをとにかく使ってください
- 運動方程式
- エネルギー保存則
円運動の問題は基本的にこれだけを使いこなされば解けます。
円運動の問題解説1:エネルギー保存則の使い方
(1)は運動方程式でもエネルギー保存則でもどちらでも解けそうな感じですね。ただ、運動方程式だと張力の情報が必要なんですが、問題文では与えられてないですね。
なので糸の張力を使わなくて済む方法を考えます。
それはエネルギー保存則です。
エネルギー保存則はこうでしたね。
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
今回の非保存力は張力のみですが、これは仕事をしませんね。
力の向きと移動向きが垂直だからです。
あとは力学的エネルギーを考えるだけでOKです。

位置エネルギーを考える必要があるので、最下点を基準に取るとエネルギー保存則に必要な情報は次のようにまとめられます。
(はじめの力学的エネルギー)= \(\frac{1}{2}mv_0^2\)
(非保存力にされた仕事)=0
(あとの力学的エネルギー)=\(\frac{1}{2}mv^2 + mgr(1 – \cos{\theta})\)
よって
\(\frac{1}{2}mv_0^2 + 0 = \frac{1}{2}mv^2 + mgr(1 – \cos{\theta})\)
\(v = \sqrt{v_0^2 – 2gr(1 – \cos{\theta})}\)
これが答えです。
円運動の問題解説2:運動方程式の使い方
(1)でエネルギー保存則を使ったので、もうやるべきことは一つですね。
運動方程式を使いましょう
運動方程式は以下のような手順で立てます。

Step 1は良いとして、Step 2ですね。
運動方程式は円の中心方向について立てるんでしたね。
そして、正の向きについては中心向きを正とする約束があったのでそれには絶対にしたがってください!!
それが分かっていればOKです。
Step 3でが、物体にはたらく力も中心方向と鉛直方向に分けて考えます。
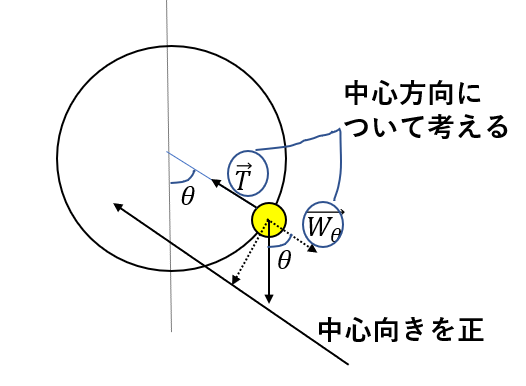
そして、力を成分表示します。
\(\vec{T} = (T)\)
\(\vec{W_\theta} = (-mg\cos{\theta})\)
Step 4
次に合力ですね。
ベクトルをとにかく足すことを忘れないように!!
\(\vec{F} = \vec{T} + \vec{W_\theta} = (T – mg\cos{\theta})\)
Step 5
運動方程式\(m\vec{a} = \vec{F}\)に成分を代入しますが円運動するときの加速度については重要なことがありましたね。
円運動するときは、中心方向に関して言えば
\(a = \omega^2 r = \frac{v^2}{r}\)
が成り立つんでしたね。
今回は\(v\)の情報を使うので
\(\vec{a} = (\frac{v^2}{r})\)
を代入します。
\(m\frac{v^2}{r} = T – mg\cos{\theta}\)
\(T = m\frac{v^2}{r} + mg\cos{\theta}\)
これが答えです。
円運動の問題解説3:円運動し続ける条件は「速さ≠0」ではない!
(3)は「1周する条件」という円運動の典型問題です。
これは最初にお見せした通りです。
1周する条件
常に中心向きにはたらく力がある
よくあるミスが「速さが0にならない」と考えることです。
「円運動しなくなるとき\(v = 0\)となるから、円運動し続けるには\(v \ge 0\)である」と考えたくなるのはわかりますが、これは間違いです。
速さを持っていても円運動しない例はあります。ですので、\(v \ge 0\)は条件ではないです。
円運動するという条件には加速度が常に中心向きに生じているというものがあります。
加速度が常に中心向きに生じるということは常に中心向きに力も生じていると言えますね。
これは運動方程式を考えれば良くわかります。

加速度が生じるということは、その向きに力が生じるということです。
円運動する条件
→加速度が常に中心向きに生じている
→常に中心向きにはたらく力がある
というわけで、最初に示した条件が成立するのです。
「常に中心向きにはたらく力」とはどういうことですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
今回の場合は、常に中心向きにはたらく力として糸の張力があります。
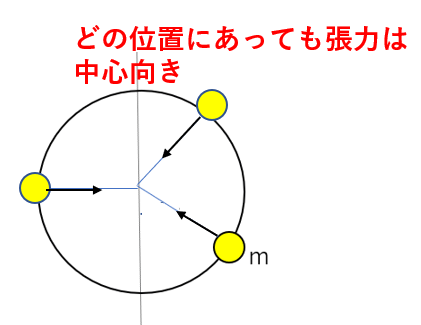
これが、「常に中心向きにはたらく」という意味で
一方、重力はどうでしょうか?
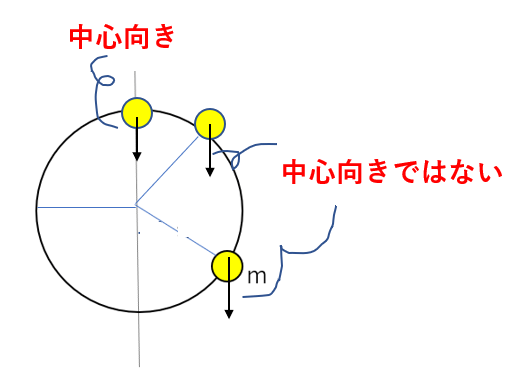
こんな感じで、常に中心向きを向いているわけではないですね。
- 張力→常に中心向き
- 重力→常に中心向きではない
とまとめられます。
なので、常に張力がはたらいている条件(糸がたるまない条件)を考えれば良いのです。
(1)、(2)から\(v\)を消去します。
\(T = m\frac{v_0^2}{r} + mg(3\cos{\theta} – 2)\)
これを見ると、\(\theta = \pi\)のとき(物体がてっぺんに来たとき)に\(T\)が最も小さくなりますね。
ですから\(\theta = \pi\)のとき、\(T \ge 0\)とすれば\(T\)が0になることは無くなり条件が導けます。
\(m\frac{v_0^2}{r} – 5mg \ge 0\)
よって
\(v_0 \ge \sqrt{5gr}\)
が答えです。
まとめ:円運動の問題の解き方
いかがでしたか?
円運動の問題の解き方いたってシンプルです。
運動方程式とエネルギー保存則を使いつつ、円運動の問題特有の「1周する条件」が分かっていればOKです。
何かあればどんどんコメントくださいね!それでは!
・円運動の問題のポイント
運動方程式とエネルギー保存則をとにかく使え!
・円運動する条件
→加速度が常に中心向きに生じている(こっちは知らないとだめ)
→常に中心向きにはたらく力がある
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!











Comment
だいぶ前の記事なのでご覧いただけるかわかりませんが、
非等速円運動の場合加速度は中心方向ではないので、少々誤解を招く書き方になっていると思います。
円運動の条件(合力がmv^2/r)と、糸がたるまない条件(T>0)を、常に同時に満たせるときに一周する
くらいでよいのではないでしょうか。