高校物理で使える微分積分まとめ。知っておくと便利な式とは?

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
高校物理で微分積分は知っておいた方が良いのでしょうか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
今回はこのような悩みを解決します。
高校物理で微分積分を学ぶかどうかを考えている人が多いと思います。
結論から言いますと、学ぶ必要は全くありません。
しかし、知っておくと本質が理解できたり、模試の解説(特に駿台)を理解しやすくなったり、入試本番でも確認のために使うこともできます。
この記事では、高校物理で使える微分積分の話をしていきたいと思います。
物理の内容はある程度理解できている人でもっと深く知りたいという方は最後まで読んで、力をつけてください!
目次
物理の公式は微分と積分で表せる

大学になると、微積で物理を扱うことが基本になります。
物理は時間変化を扱っていくので、微分を使うことはイメージできると思います。
そして、実際に物理の公式は微分積分ですべて表すことができます。
高校で出てきた公式も微分積分を具体的に計算した形になっていたり、変化量\(\Delta\)を使ってごまかして表しているだけで、本来ならすべて微分積分の形で書けます。
物理の公式がなぜ微分積分の形で書けるかというと、ほとんどの公式は運動方程式から導くことができ、その運動方程式が微分の形で表されているからです。
ここから高校物理でも知っておきたい微分積分の関係を見ていきましょう!
物理の微分積分1:位置、速度、加速度

まず、位置、速度、加速度についてです。
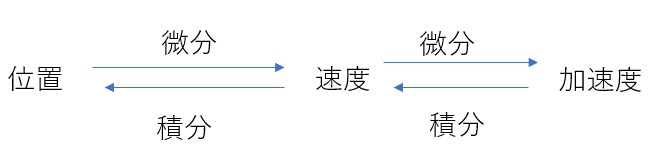
結論から言うと、これらには以下のような関係があります。
平均の速さ
このような関係になる理由を説明します。
速さは「距離÷時間」と表せると学びました。
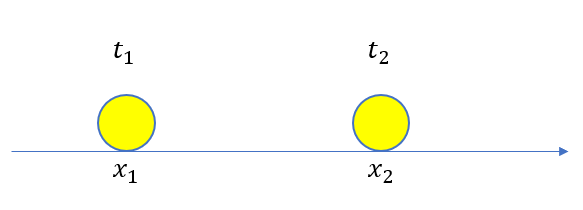
移動距離\(\Delta x\)、時間\(\Delta t\)を用いると速さは
\(v = \frac{\Delta x}{\Delta t}\)
と表せます。
これは「平均の速さ」と呼ばれていますが、一つ問題があります。
ある一瞬の速さがわからないのです。
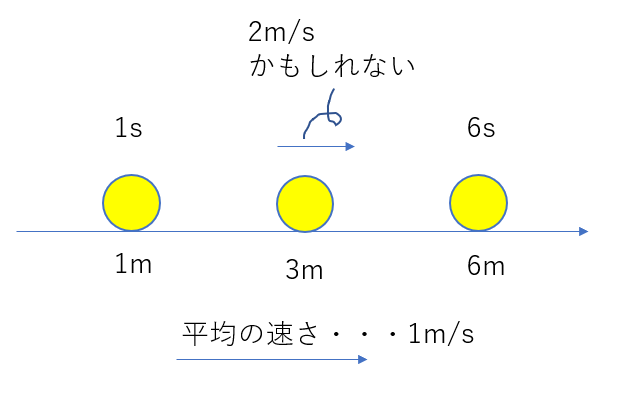
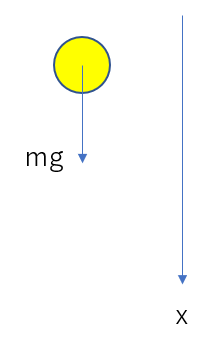
図のような状況では平均の速さは1m/sです。これは常に1m/sという速さで動いたという仮定をしているだけです。
もしかしたら途中2m/sの速さで動いているかもしれません。が、これが求められないのです。
瞬間の速さを求めるために微分を使う
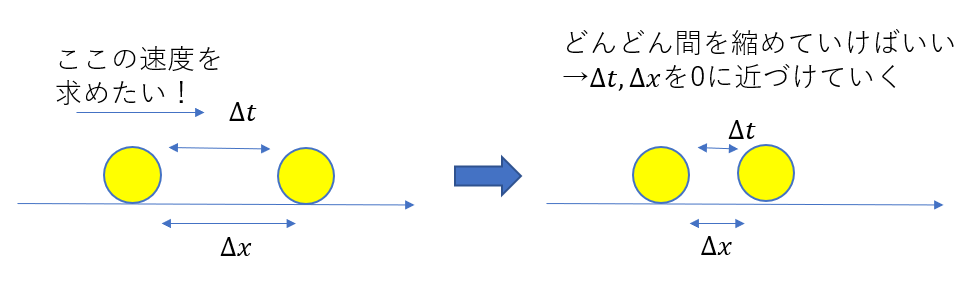
もし先ほどの途中にある速さを求めるには、時間や移動距離を小さくしていく必要があります。
このように、どんどん時間を小さくしていくことで、各瞬間の速さを求めることができるのです。
ある瞬間の速さを求めたいなら\(\Delta t \to 0\)を考えれば良いのです。
\(\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}\)
このように、極限の形になり、これは微分の定義そのものなのです。
\(v = \frac{dx}{dt}\)
つまり時間\(t\)での速さ\(v\)は、位置を時間\(t\)で微分することで得られます。
加速度も同じで、\(x\)を\(v\)で置き換えれば良いのです。
\(a = \frac{dv}{dt} = \frac{d^2x}{dt^2}\)
つまり、最初に見せたような関係が成り立つのです。
運動方程式と微分積分

加速度が微分の形で書けたので、運動方程式も微分の形で書くことができます。
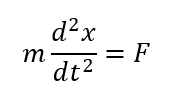
このように微分を含んだ方程式のことを微分方程式と言います。
高校の公式はこれを解くことによって得ることができます。
いくつか微分形の運動方程式を使ってみます。
等加速度運動の公式と微分積分
まず、運動方程式を立ててみます。
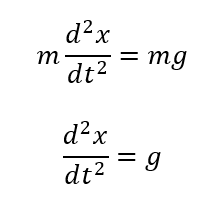
この方程式を解くことによって位置や速度が求められます。
\(v = \frac{dx}{dt}\)なのでこの式は次のように置き換えられます。

これは「\(v\)を\(t\)で微分したら\(g\)になりますよ」という意味です。
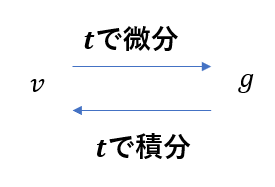
つまり、このように\(g\)を積分したら\(v\)になるということです。
これを踏まえて\(v\)を求めてみましょう。
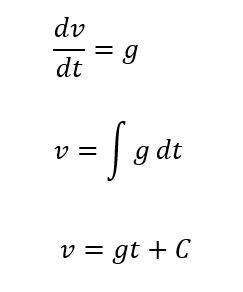
このように表すことができます。
\(C\)は定数です。これは\(t=0\)のときの速度、つまり初速度です。これを\(v_0\)と置けば
\(v=v_0+gt\)となり、まさに等加速度運動の公式になりますね。
そして\(v = \frac{dx}{dt}\)とすれば同じように位置\(x\)を求められます。
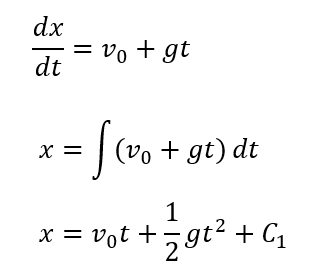
\(C_1\)は定数です。これも\(t=0\)の位置、つまり初期位置になります。
これを\(x_0\)と置けば
\(x=x_0+v_0t+\frac{1}{2}gt^2\)
となり、等加速度運動の公式そのものです。
このように、等加速度運動の公式を暗記させられていましたが、運動方程式を解いた結果に過ぎなかったのです。
単振動と微分積分
ばね定数\(k\)のばねに取り付けられた質量\(m\)の物体の時刻\(t\)における位置を求めよ。
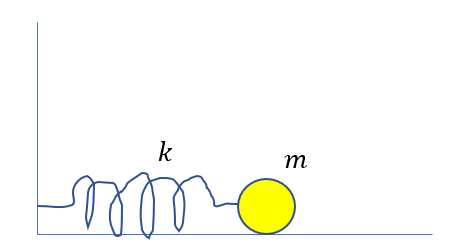
今度は水平ばねの単振動を見てみましょう。
運動方程式を立ててみます。
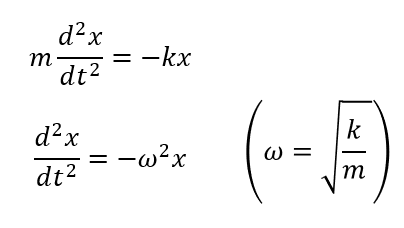
(\(\omega\)をこのようにおいた理由は後ほどわかります)
これは先ほどのように単純に積分して解けるわけではありません。あるテクニックを使います。
微分含め、\(x\)だけの式で表されている場合は\(x = Ce^{\lambda t}\)という解になることが分かっています。
上の式は「\(x\)を微分したら\(x\)になる」という式なので、微分しても変わらない関数、つまり\(e^t\)の関数になることが予測できるからです。
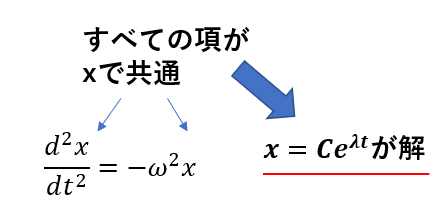
これが解と分かっているのでこの方程式に代入してもOKです。
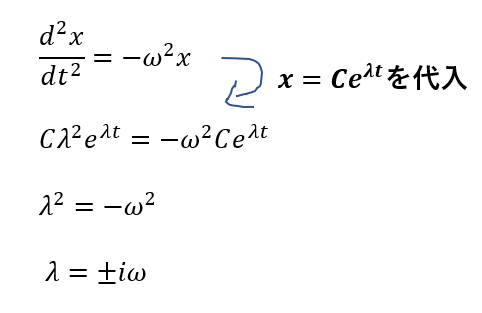
するとこのように\(\lambda\)が求まります。\(\omega^2\)としておいたのは最後の式変形で見やすくするためです。
\(\lambda\)が2つ出てくるので、それぞれを使って
\(x_1 = C_1e^{i\omega t}, x_2 = C_2 e^{-i\omega t}\)とします。
するとこれらを足した
\(x = x_1 + x_2\)
も方程式の解になることが分かってます。実際に代入して見ると方程式を満たします。
なのでこの\(x\)を計算することで位置が求まります。
ここで
\(e^{\pm i\theta} = \cos{\theta} \pm i\sin{\theta}\)
という公式があります。
これを使って\(x\)を求めてみると・・・

このように求めることができます。
例えば\(t=0\)で初期位置が原点\(x=0\)であれば、\(A=0\)となりますので
\(x=B\sin{\omega t}\)
とまさに単振動の位置の式が出すことができます。
微積が使えると「運動方程式を解く」ことができ、「等加速度運動」や「単振動」、そして「名前のない運動」など場合分けをしなくても速度や位置の式を求めることができるのです。
仕事と微分積分

仕事も微分積分で表すことが普通です。
入試問題を解いた人なら一度はやったことあると思います。
「微小変化を考えて足していく」ということを。
微小変化を扱うことについてはコチラで詳しく説明しています。
例えばばねの弾性エネルギーを考えるときはこの考え方を使って導出できました。
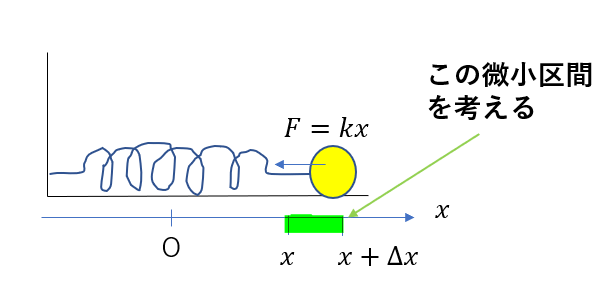

この考え方は実は積分そのものですよね(区分求積法と一緒です)。
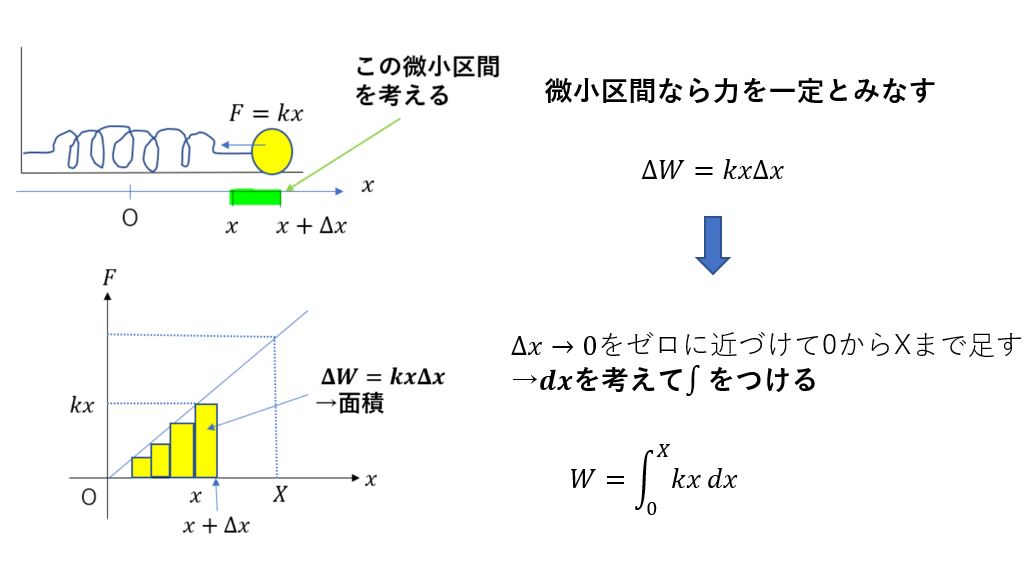
最後の全仕事\(W\)がまさに積分になっていますね。

このように、仕事は積分を使って一般的に表すことができるのです。
積分を使わないと力が一定のとき「力×距離」でしか求められませんが、積分を使えば力が変化しても求めることが可能です。
微分と積分の図形的な意味

最後に微分積分の図形的な意味を教えておしまいにします。
数学でも習った通り、微分は接線の傾き、積分は面積を表します。
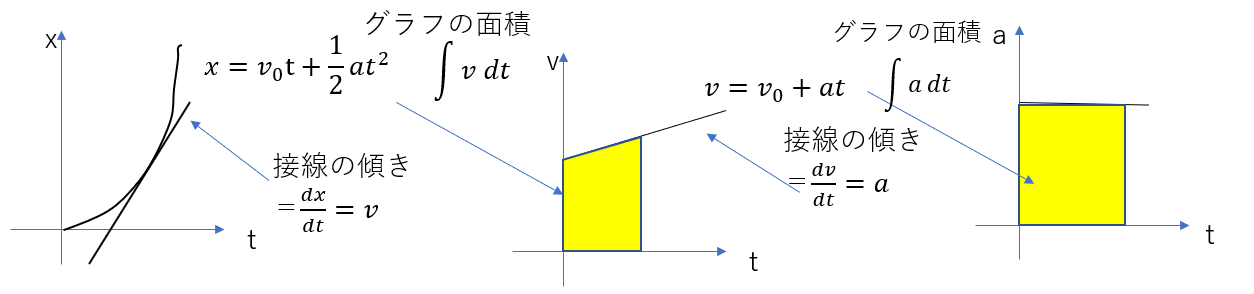
等加速度運動の式を例に出すと
\(x\)を\(t\)で微分すると\(v\)になることと、微分がグラフの接線の傾きであることを踏まえると、x-tグラフの接線の傾きが瞬間の速さ\(v\)となることが分かります。
またv-tグラフの接線の傾きが加速度\(a\)になることも同じように分かります。
逆にa-tグラフの面積を求めれば\(v\)になり、v-tグラフの面積を求めれば\(x\)になります。
微分積分は図形的にもこのような意味を持ちます。
まとめ:物理の式は微分積分でできている

いかがでしたか?
今まででてきた公式はすべて微分積分で表すことができます。
しかし、見ての通り内容が重いですし、高校生では微分方程式は必修ではないので微積を使わなきゃ解けない問題は出ません。
なので微分積分は+α程度にしておくことをおすすめします。