ドップラー効果の公式は波の個数問題だった!簡単な覚え方を教えます!

Akinoriさん。ドップラー効果が全くわかりません!波長が短くなるとかどうとか・・・
 AI
AI
ドップラー効果ってイメージがしにくいよね。
 AKINORI
AKINORI
あと、公式もいまいち分からないんです!
 AI
AI
じゃあ、ドップラー効果をちゃんと理解して、公式も導いてみよう!ドップラー効果ではあることに注目すると理解できるよ!!
 AKINORI
AKINORI
ドップラー効果はイメージがしにくくて、高校生泣かせな単元ですね。
意味わからず公式だけ覚える。
そんな苦行を強いられる人も少なくないと思います。
なので、ここで超わかりやすく説明したいと思います。
ドップラー効果って何?
ドップラー効果というのは波に特有の現象です。
よく例に出てくるのが、救急車のサイレンですね。
救急車が近づいてくるときは音が高く聞こえて
遠ざかるときは音が低く聞こえる。
これがドップラー効果です。
音源が動くことによって、波長が変わります。
波の基本式\(v = f\lambda\)より、
波長が変われば、当然ですが振動数\(f\)も変化します。
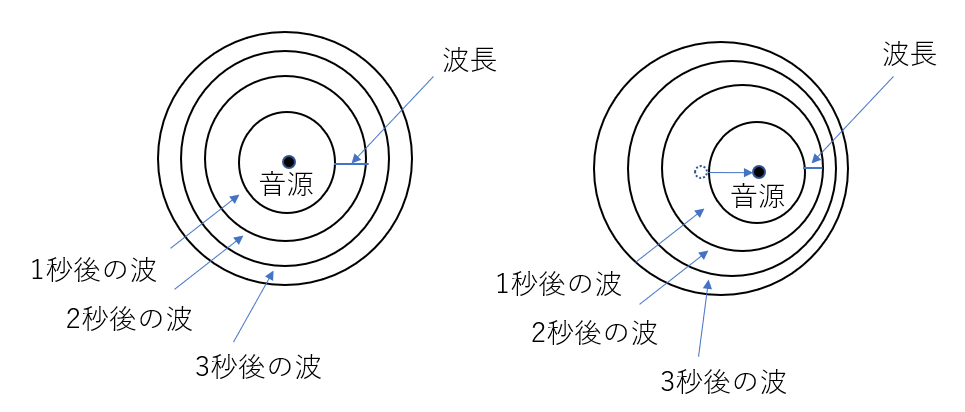
という感じで、波長が伸びる縮む。
こういう説明をされるんですが、
・・・・・
全くイメージができない!!

なので、別の視点からドップラー効果を考えたいと思います。
波の個数に注目!!
その視点はズバリ、
波の個数
です。
波の個数を考えることについてはこちらの記事で触れています。
振動数\(f\)の意味は
「1秒間に\(f\)個の波を出す」
という意味でした。
この波の個数を考えるとドップラー効果が理解しやすいです。
いくつか例を出してみましょう。
例1:音源が動く場合
まずは、音源が動く場合です。
音源が止まっている観測者に向かって、一定の速さ\(v\)で動いている。この音源の振動数を\(f_0\)、音速を\(V\)としたとき、観測者が聞く音の振動数を求めよ。

1秒間で考えてみましょう。
音速が\(V\)なので、一秒間で音は\(V\)の長さだけ進みます。
また、振動数が\(f_0\)なので、1秒間で\(f_0\)個の波が出ます。
もし、音源が止まっているなら当然ながら、
\(V\)の中に\(f_0\)個の波が含まれますね。

わかった!実際は音源自体が\(v\)だけ進むから波が含まれる長さが違うんですね!
 AI
AI
そう!でも振動数は音源特有のものなので変わらないよ。
 AKINORI
AKINORI
今回は音源が速さ\(v\)で動くので、この1秒間で\(v\)の長さだけ進みます。
なので、実際に含まれる波の長さは\(V\)ではないです。
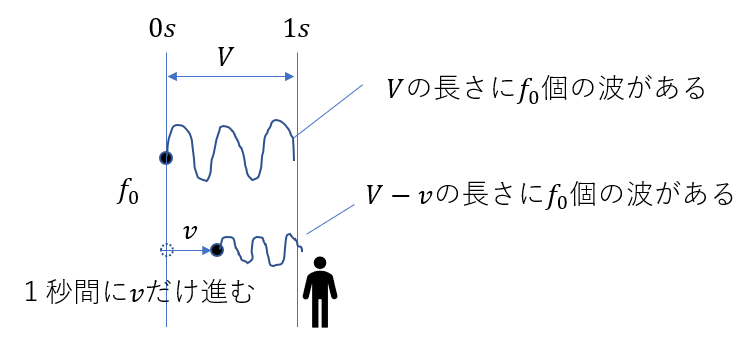
図のように\(V – v\)の長さに波が含まれます。
波の含まれる長さが変わっているのです。
ただ、振動数は動いていようが\(f_0\)で固定です。
振動数は音源の種類で決まるので変わるはずがないのです。
つまり、
「\(V – v\)の中に\(f_0\)個の波が含まれる」
と言えますね。
イメージしやすいと思いませんか??
これで、音源が出す音の波長が求められます。
波長は「波一個の長さ」だから、全長を波の個数で割ればいいんですね!
 AI
AI
なので、音源が出す音の波長は
\(\lambda’ = \frac{V – v}{f_0}\)
となります。
じゃあ、実際に観測者が聞く振動数\(f\)はどうなるでしょう?
やっぱり波の個数を考えるんですよね?
 AI
AI
もちろん!!
 AKINORI
AKINORI
観測者は動いていないから\(V\)の長さだけ音を聞きますね。
ただし、その音の波長は\(\lambda’\)です。さっき求めたやつね。
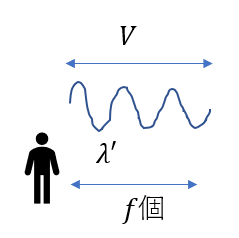
波長\(\lambda’\)の波が\(V\)の中に\(f\)個含まれる。
ということなので、
\(V = f\lambda’\)
波の基本式ですね。
\(f = \frac{V}{V – v}f_0\)
これが観測者の聞く音の振動数です。
音源の振動数\(f_0\)と観測者が聞く音の振動数\(f\)は値が違ってますね。
 AI
AI
さらに言えば、\(f > f_0\)なので、音が高く聞こえるってこと。救急車が近づいている状況と同じだね。
 AKINORI
AKINORI
観測者が動く場合
では、次は観測者が動く場合です。
観測者が止まっている音源に遠ざかって、一定の速さ\(u\)で動いている。この音源の振動数を\(f_0\)、音速を\(V\)としたとき、観測者が聞く音の振動数を求めよ。
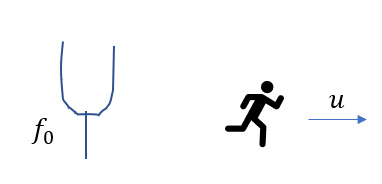
同じように、波の個数に注目して考えます。
1秒間で考えると
音源は止まっているので、今回は
\(V\)の長さに\(f_0\)個の波が含まれる

なので、音源が出す音の波長は
\(\lambda ‘ = \frac{V}{f_0}\)
ですね。
次に観測者を考えたいんですが、
今回観測者は動いているので、音の聞く範囲、つまり
音が含まれる範囲が変わっています。
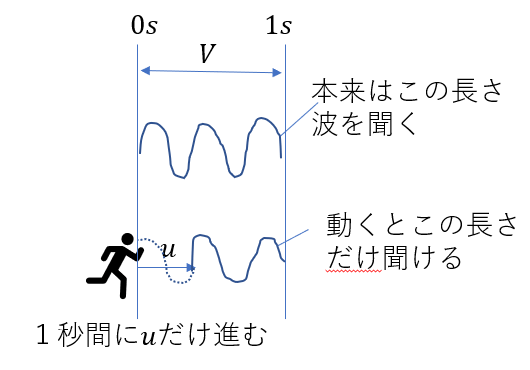
1秒で\(u\)だけ進んでしまうので、聞く長さが\(V – u\)になるってことですね。
つまり
波長\(\lambda ‘ \)の波が\(V – u\)の中に\(f\)個含まれている
\(V – u = f\lambda’\)
やっぱり波の基本式ですね。
\(f = \frac{V – u}{V}f_0\)
簡単に求められた!
 AI
AI
これは音が低く聞こえるのがわかるね。
 AKINORI
AKINORI
音源も観測者も動く場合
じゃあ、最後に両方が動く場合を考えてみましょう。
音源が速さ\(v\)で、観測者が速さ\(u\)で、互いに近づく向きに動いている。音源の振動数を\(f_0\)とし、観測者が聞く音の振動数を求めよ。ただし、音速は\(V\)とする。

もちろん、波の個数に着目していきます。
今までと同じですね。
音源が出す波に関しては
\(V – v\)の中に\(f_0\)個の波が含まれる
ということです。

なので、波長は
\(\lambda’ = \frac{V – v}{f_0}\)
今度は観測者ですが、これも同じです。
\(V + u\)の中に\(\lambda’\)の波長の波が\(f\)個含まれます。
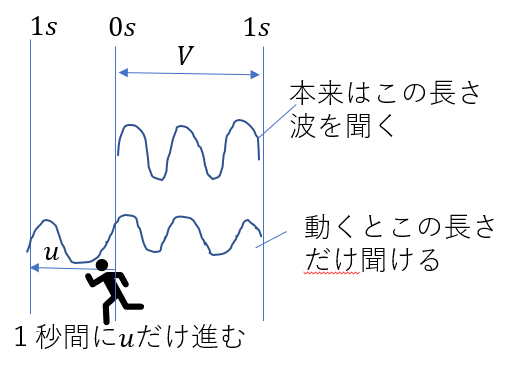
つまり
\(V + u = f\lambda’\)
\(f = \frac{V + u}{V – v}f_0\)
これが、観測者が聞く音の振動数ですね。
要は、波の個数を考えれば解けるってことですね!
 AI
AI
そう!ただ、いちいち考えるのも面倒なので、とっておきの公式を教えるよ!
 AKINORI
AKINORI
ドップラー効果の最強公式
と、ここまで例を見てきたんですが、
どの例でも共通して言えることがあります。
もちろん波の個数を見てきたことです。
ですが、もっと見てみると・・・
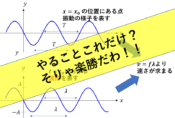
矢印の長さで決まる!!??
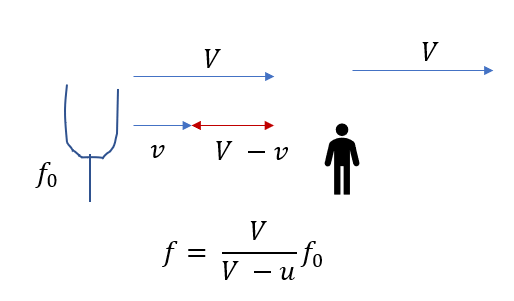
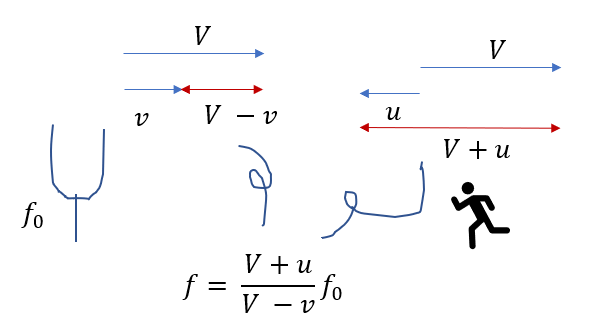
お~!音源や観測者に関する速さの矢印の長さを分数にすれば出来上がり!!
 AI
AI
これをドップラーの公式として覚えてもいいよ!
 AKINORI
AKINORI

これを使えばだいたいのドップラー効果の問題は解けるので、かなり時短になります。
めちゃめちゃ使い勝手がいいので使ってください!
まとめ
- ドップラー効果
波の個数に注目すればよい!!
- ドップラー効果の公式
\(f = \frac{観測者の矢印}{音源の矢印}f_0\)
公式の分数の上下が分からなくなることが多いので、こう覚えておいてください!
観音様
文字通り上から並べればOKです!!
ということで、ドップラー効果でした。









Comment
「1秒間にf個の波を出す」のがよくわからなかったので記事に飛んだのですがその記事のどこら辺に書いてあるのか見つけられないのですが。。
天才だと思いました。
天才的