電磁誘導の問題解説！やるべきことは公式利用、それだけ！！

2019年3月17日

WRITER

あっきー

　

この記事を書いている人 - WRITER -

あっきー

オンライン物理塾長あっきー。高3秋から1か月で40点点上げ、センター試験では満点を取り、その経験を活かし塾講師として活躍。塾・学校・参考書の内容やカリキュラムに違和感を感じ数多くの高校生を救うため、大学2年生で「受験物理Set Up」を開設。多くの高校生が活用するサイトに発展し、現在「合格への道」で勉強法に特化した受験サポートを行う。

電磁誘導についてはこちらをチェックしてください！

電磁誘導のマイナスって何よ！困らない起電力の向きの求め方。

電磁誘導のポイントはズバリ

磁束の変化

です。

磁場の変化ではなく、磁束の変化です。

そして、磁束が変化すると回路には起電力が生じるのですが、この起電力は

• 大きさ
• 向き

と二つのステップを分けて求めていきましょう！！

問題

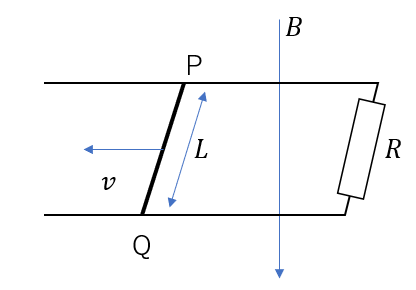
図のように、下向きに一様な磁場が生じている。回路には抵抗\(R\)がついていて、長さ\(L\)の金属棒PQは回路上を滑らかに動くことができる。この金属棒を一定の速さ\(v\)で左向きに動かす。

(1)　生じる起電力の大きさを求めP,Qのどちらの電位が高いかを求めよ

(3)　金属棒が一定の速さ\(v\)で動くために必要な外力の大きさと向きを求めよ。

(4)　時間\(\Delta t\)の間に、外力がした仕事と、抵抗で発生したジュール熱をそれぞれ求めよ。

（１）磁束の変化は何で決まる？

起電力の大きさはファラデーの電磁誘導の法則を使えば良いですね。今回、巻き数が１なので

\(|V| = |\frac{\Delta \Phi}{\Delta t}|\)

です。

では、\(\Delta t\)の間の磁束の変化を考えてみましょう。

金属棒PQを図の向きに一定の速さ\(v\)で引っ張るので、\(v\Delta t\)の距離だけ動きますよね。

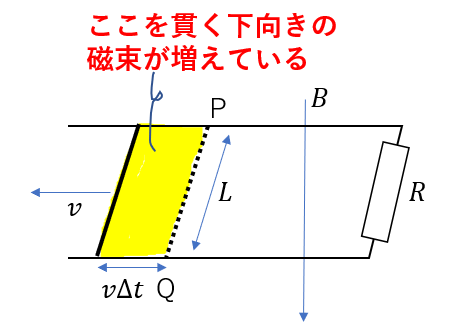
つまり、色のついた部分を貫く磁束が\(\Delta \Phi\)に当たるわけです。

磁束は

\(\Phi = BS\)

つまり、「磁束密度×面積」

ですので、

\(\Delta \Phi = B\cdot v\Delta t L\)

ということで起電力は

\(|V| = |\frac{Bv\Delta t L}{\Delta t}| \)

∴\(V = vBL\)

と書けますね。

今、下向きの磁束が増えているので、回路は上向きに磁束を作ろうとします。

上向きに磁束を作るには、電流は上から見て

反時計回り

に流れる必要があります。

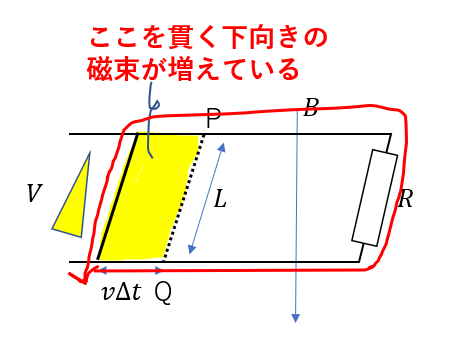
ということで向きはP→Q向きですね。

まとめると、

起電力：\(V = vBL\)

電位：Pの方が高電位

（２）電流が流れると、金属棒は力を受ける！

電流が受ける力は

\(F = IBL\)

です。

この力がかかるので、これにつり合うように外力を加えないと

一定の速さ\(v\)で動かすことができませんね。

なので、まずは電流を求めましょう。

キルヒホッフの法則から

\(V – IR = 0\)

∴\(I = \frac{vBL}{R}\)

ですね。

金属棒が磁場から受ける力の大きさは

\(F = IBL = \frac{vB^2L^2}{R}\)

です。

向きは、「FBIは左利き」でしたね。

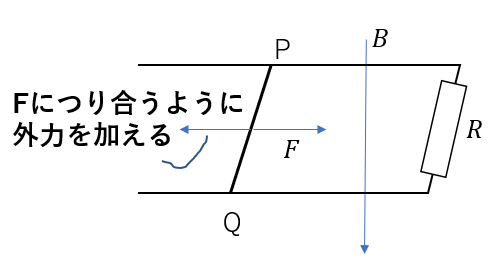
なので、求める外力は

大きさ：\(F = \frac{vB^2L^2}{R}\)

向き：左向き

（３）結果は「エネルギー保存則」を示す！！

これは普通に計算しましょう。

外力がした仕事ですが、

今回の外力は一定ですよね？

つまり「力×距離」として求めることができるわけです。

\(\Delta t\)の間には距離\(v\Delta t\)の距離を力の向きに進むので

\(W = F\cdot v\Delta t = \frac{(vBL)^2}{R}\Delta t\)

と仕事は表せます。

一方ジュール熱は

\(Q = IVt\)

と書けます。

これについてはこちらを見てください。

白紙から説明せよ！電流の電子モデル化で定義I=vsneを導出！

今まで求めた\(I, V\)を代入すれば

\(Q = \frac{(vBL)^2}{R}\Delta t\)

と表せます。

金属棒が外力から仕事をされれば「エネルギー原理」から、運動エネルギーが変化するはずですよね？

ですが、\(v\)は一定ですから、運動エネルギーは変化していません。

これだと

「外力がしたことで生まれたエネルギーがどこに行っちゃったの？？」

ってなりますよね？

このエネルギーは

起電力を作り電流を流すエネルギーに変わっています。

そして、このエネルギーは抵抗に対して仕事をして、ジュール熱として変わっています。

外力の仕事→ジュール熱

となっているわけですね。

ですから、答えが同じになるのも当然なんです。

いかがでしたか。

基本は、

磁束が変化するところに起電力あり

です。

電磁誘導と来たら、使える式はファラデーの電磁誘導の法則

\(V = -N\frac{\Delta \Phi}{\Delta t}\)

です。

あとは、大きさ→向きという順番で求めればOKです。

電磁誘導の問題も良く問われます。しっかりマスターしておきましょう！！