【物理基礎】摩擦力の求め方と使い方【滑らない条件を分かりやすく】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
今回は摩擦力についてお話をしていきます。摩擦力はそこまで難しくありませんが、
・静止摩擦力と最大摩擦力の違いは?
・滑らない条件って何?
これらを解決していきたいと思います。
それでは、いってみよう!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
目次
摩擦力とは?
摩擦力は物体同士が表面で平行に及ぼしあう力です。
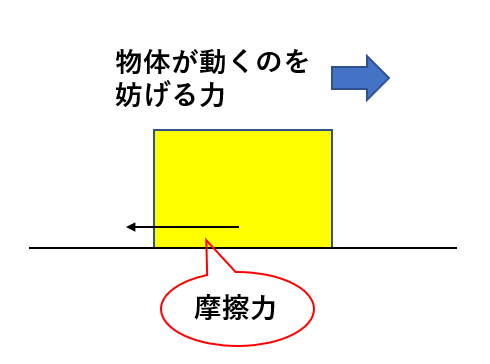
物体が動く(動こうとする)向きとは逆にはたらきます。
摩擦力は作用反作用の関係にあるので、特に2物体が及ぼしあって運動する場合は向きに注意が必要です。
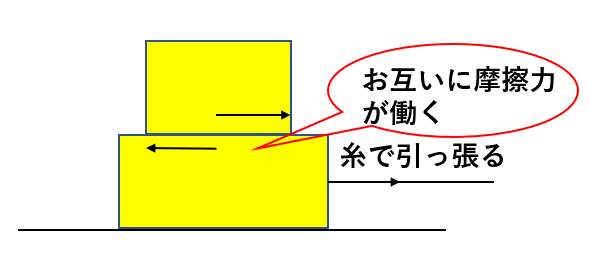
例えば、2物体の間で摩擦力がはたらくときは下の物体は左向きに摩擦力がはたらきます。作用反作用なので、上向きの物体は同じ大きさで右向きに摩擦力が働きます。
摩擦力を書き忘れたり、向きを間違えたりしないように注意しましょう。
摩擦力には2種類ある
摩擦力には2種類あります。
- 静止摩擦力
- 動摩擦力
静止摩擦力
静止摩擦力は物体が動き出す前に働く力です。
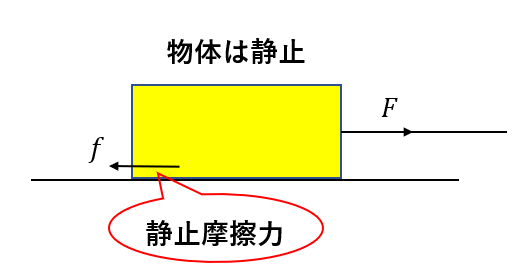
外力を加えてもこの摩擦力によって力がつりあって静止します。
この静止摩擦力は式に表すことはできませんが、物体を引く力\(F\)に比例します。
そして、静止摩擦力はある値を越えると、物体が動き出し動摩擦力となります。
この静止摩擦力が最大となるときを最大摩擦力と言います。
動摩擦力
動摩擦力は物体が動いているときに働きます。
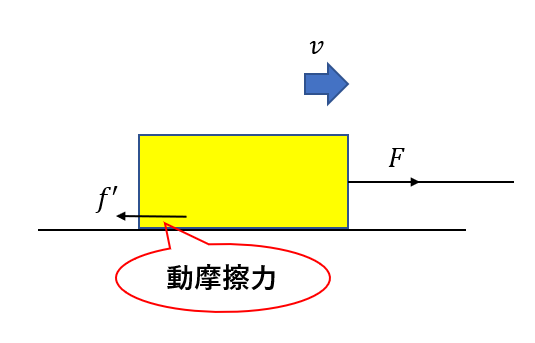
動摩擦力は静止摩擦力とは異なり、式で表すことができ一定の値と取ります。
重い荷物を引っ張るとき、動き出してからはスムーズに動いたという経験ありませんか?
あれは最大摩擦力よりも動摩擦力の方が小さくなり、加える力が小さくなるからです。
動摩擦力と最大摩擦力の公式
摩擦力は最大摩擦力と動摩擦力は式で表すことができます(静止摩擦力は式で表せません)。
最大摩擦力
\(f_0 = \mu N\)
動摩擦力
\(f’ = \mu’ N\)
(\(\mu\):静止摩擦係数 \(\mu’\):動摩擦係数 \(N\):垂直抗力の大きさ)
動摩擦力は最大摩擦力より小さいので、\(\mu’ < \mu\)となります。
摩擦力の公式の\(N\)には注意
この\(N\)ですが、これは垂直抗力です。
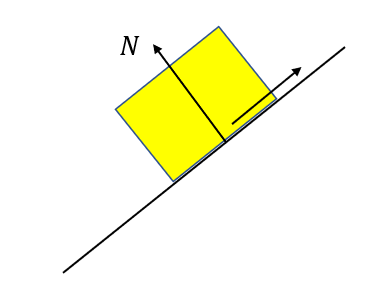
例えば、図の摩擦力を求める際には図のような垂直抗力の大きさ\(N\)を使います。
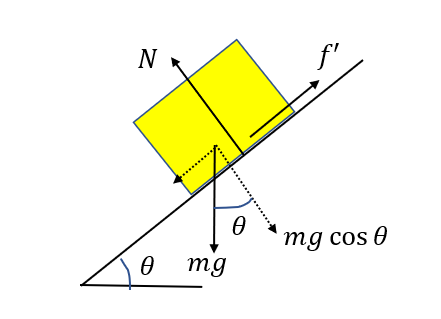
斜面に垂直方向の力のつり合いを考えると\(N = mg\cos{\theta}\)となるので、動摩擦力は
\(f’ = \mu’ mg \cos{\theta}\)
となります。
たまに\(mg\)をそのまま使ってしまう人がいますので注意しましょう。
また、あくまで\(N\)を使うので、斜面でなくてもいつも\(N=mg\)として摩擦力を使うわけではありません。
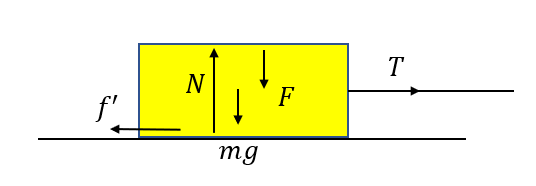
この場合、鉛直方向の力のつり合いから\(N = mg + F\)なので、動摩擦力は
\(f’= \mu’ (mg + F)\)
となります。
常に\(f’= \mu’ mg\)となるわけではないので注意しましょう。
静止摩擦力と動摩擦力のグラフ
動摩擦力と静止摩擦力の関係をグラフにすると以下のようにあります。
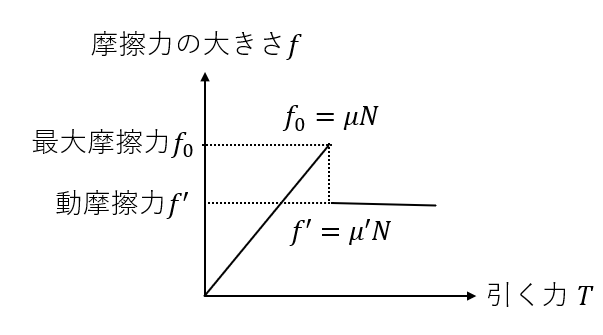
静止摩擦力は引く力に比例します。
そしてある値\(f_0 = \mu N\)で最大摩擦力となり、そのあとは、動摩擦力\(f’ = \mu’ N\)となり一定になります。
動摩擦力は最大摩擦力より小さくなることもわかりますね。
最大摩擦力と静止摩擦力の違いとは?
たまにある質問で、「最大摩擦力と静止摩擦力の違いって何?」というのを聞きます。
これは先ほどのグラフを見ればわかりますね。
静止摩擦力は「静止している物体にはたらく力」です。
その中で最大の値を取るときを特別に「最大摩擦力」と言います。
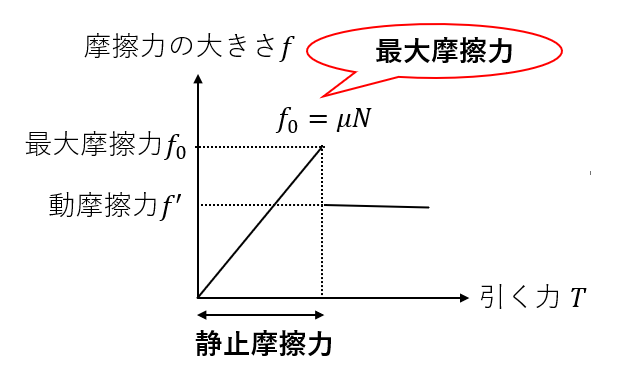
式で書けるのは最大摩擦力です。静止摩擦力は式で書けず、単純に「引く力とつり合っている」という式しか書けません。
摩擦力を使った滑らない条件とは?
摩擦力を使う問題として「滑らない条件」があります。
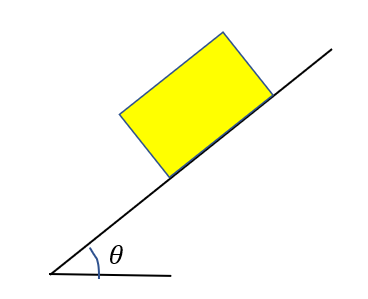
例えば、「斜面にある物体が滑り落ちないための\(\theta\)条件を求めよ」という問題があるときにこの摩擦力の条件を使います。
先ほど見たように、最大摩擦力が物体が滑り出す境目になるわけです。
最大摩擦力は静止摩擦力の最大のでしたね。
つまり、摩擦力がこの最大摩擦力より小さければ滑らないということがわかります。
このような場合は、「最大摩擦力で物体が静止している」とまずは考えると良いです。
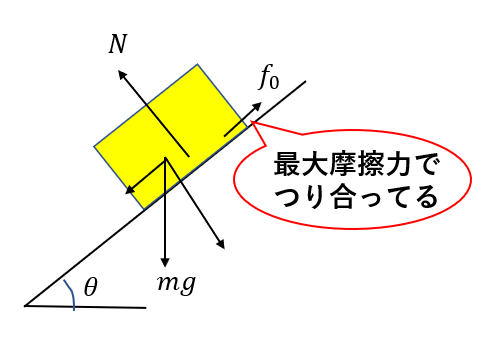
\(f_0 = \mu N = \mu mg\cos{\theta}\)となります。
水平方向に関して力のつり合いを考えれば
\(mg \sin{\theta} = \mu mg \cos{\theta}\)
\(\tan{\theta} = \mu\)
これが最大摩擦力に達してギリギリ滑らない状況の\(\theta\)の条件です。
\(\theta\)はこれより小さくなれば滑りませんよね。
\(\theta\)が小さくなるということは、\(\tan{\theta}\)も小さくなるということです。
つまり、滑らない条件は
\(\tan{\theta} < \mu\)
となります。
(ちなみに\(\tan{\theta}= \mu\)となる\(\theta\)を摩擦角と呼んだりします)
このように「滑らない条件」として最大摩擦力を使うので理解しておきましょう
まとめ
いかがでしたか?
・静止摩擦力と最大摩擦力の違い
・「滑らない条件」の求め方
これらが分かりましたね。
摩擦力は常に出てくるので、しっかり復習しておきましょう!
最大摩擦力
\(f_0 = \mu N\)
動摩擦力
\(f’ = \mu’ N\)
(\(\mu\):静止摩擦係数 \(\mu’\):動摩擦係数 \(N\):垂直抗力の大きさ)
「滑らない条件」の求め方
→「最大摩擦力で静止」を考える