運動量保存則とは?導出とエネルギー保存則との違いをわかりやすく

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
運動量保存則とエネルギー保存則の違いが分からなかったり
運動量保存則の内力とはどういう意味か分からない
という悩みはありませんか?
運動量保存則とエネルギー保存則は実はものすごく似ています。
決定的な違いはベクトルかどうかです。
逆に言えばそれだけの違いしかないため、エネルギー保存則と関連させて覚えてしまえば運動量保存則を使いこなすことができます。
実際に僕はセンター試験で満点を取り、早稲田大学に合格をしています。
今回は、運動量の正体を知るとともに、運動量保存則とエネルギー保存則の関係性を暴露したいと思います。
この記事を読み終えると運動量保存則とエネルギー保存則を使った問題を簡単に解くことができるので最後まで読んでくださいね。
運動量の真の定義が分かる
真の運動量保存則が分かる
エネルギー保存則との関係が分かる
目次
運動量の定義とは

まず、「運動量とは?」というお話からします。
運動量の定義は多くの高校生が間違って覚えているので、しっかりチェックしましょう!
質量\(m\)、速度\(\vec{v}\)の物体の運動量\(\vec{p}\)はこう定義される。
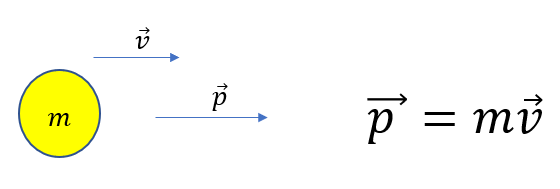
今まで\(mv\)とただ覚えていて、\(v\)が速度なのか速さなのか全く意識してなかったのではありませんか?
今回は見ての通り速度です。つまりベクトルなんです。向きがあります。
それを強調して\(mv\)ではなく\(m\vec{v}\)が正しい定義です。
そんなのどうでもいいじゃないですか~
 リケジョになりたいAIさん
リケジョになりたいAIさん
AIさん!それ危険だよ!
 あっきー
あっきー
たかが矢印一つの違いかもしれませんが、この違いで受かるか落ちるか決まるといっても過言ではないです。
実際、とある入試問題の運動量の問題があったんですが、その問題では定義がちゃんとわかっていないと全滅するような問題を見たことがあります。
僕も高校生の時にその問題に出会って爆死しました。本番じゃなくてよかった・・・って思いましたね。
運動量の定義がしっかりわかっていなかったために、符号ミスが起こって0点。
問題文で「それぞれ質量\(m,M\), 速度\(v,V\)の2物体が互いに逆向きに運動している」と与えられていて、
「この物体の運動の和を求めよ」となったときに・・・・
それぞれ逆向きに動くから一方をマイナスにして\(mv – MV\)だね
・・・・・
としてはいけませんよ!!
その具体的な話はこちらの記事で紹介で紹介しますので確認してくださいね!
運動量保存則1:運動量と力積の関係はエネルギーにそっくり

定義をしたので、次は運動量と力積の関係を見ていきましょう!
質量\(m\)の物体が一定の力\(\vec{F} = (F)\)を受けている。この力を時間\(\Delta t\)だけ受けて、物体の速度が\(\vec{v_1} = (v_1)\)から\(\vec{v_2} = (v_2)\)に変化した。この時、運動量の変化について考えよ。
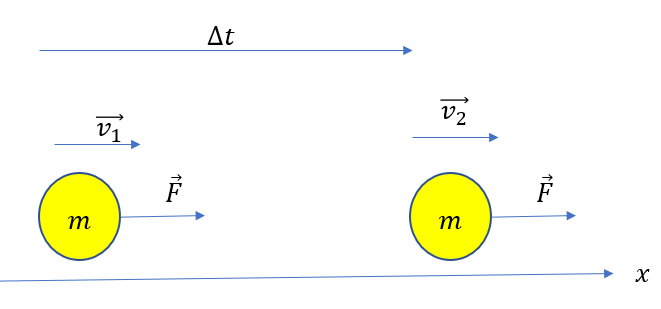
やっぱり気になるのは「力が一定」ってところですね。
これを利用しない手はないです。
これを利用するために運動方程式を立てましょう。(困ったらとりあえず運動方程式を立てよう)
\(m\vec{a} = \vec{F}\)より
\(\vec{a} = \frac{\vec{F}}{m}\)
今回は訳ありで、ベクトルのまま式変形しています。もちろん、成分を代入して式をいじるのが一番いいんですが、今回はこれでいきます。
さてさて、「\(\vec{F}\)=一定」ですよね。
\(\vec{a} = 一定\)
加速度が一定ってきたらもうあれを瞬時に思い浮かべてください!
等加速度運動の公式です。(等加速度運動の公式についてはこちらです)
今回は速度について知りたいので3つの式のうち
\(\vec{v} = \vec{v_0} + \vec{a}t\)
を使いましょう。
\(\vec{v_2} = \vec{v_1} + \frac{\vec{F}}{m}\Delta t\)
\(m\vec{v_1} + \vec{F}\Delta t = m\vec{v_2}\)
さて、この式を詳しく見ていきましょう。
まず\(m\vec{v_1}, m\vec{v_2}\)はそれぞれ運動量ですよね。
じゃあ、\(\vec{F}\Delta t\)は何でしょう?
これは「力積」と呼ばれるもので、意味は
「どれくらいの時間、力を与えましたか?」
っていうことです。
それを踏まえて、もう一度導いた式を眺めてみましょう。

なんか、すごいきれいな関係式が出てきましたね。
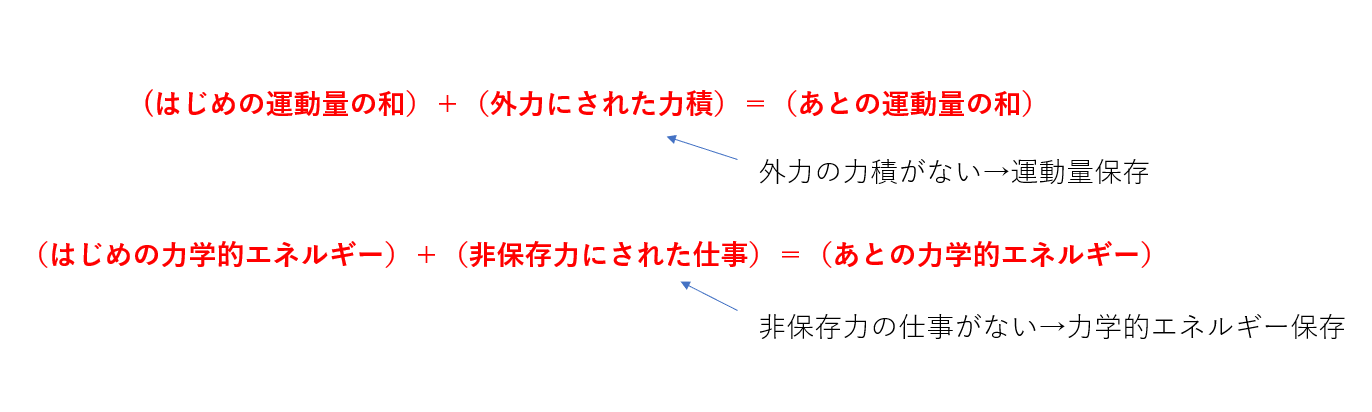
(はじめの運動)+(された力積)=(あとの運動量)
「力積を受ければ運動量が変化する」
ってことです!
あれ?似たような関係をどっかで見たような・・・?
 AI
AI
そうだね。これはエネルギーと仕事の関係(エネルギー原理)に似ているね。
 AKINORI
AKINORI
エネルギー保存則(エネルギー原理)はこういう関係のことをいいます。
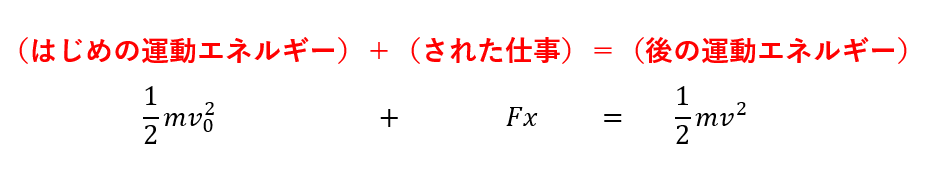
いや、似すぎですよ(笑)
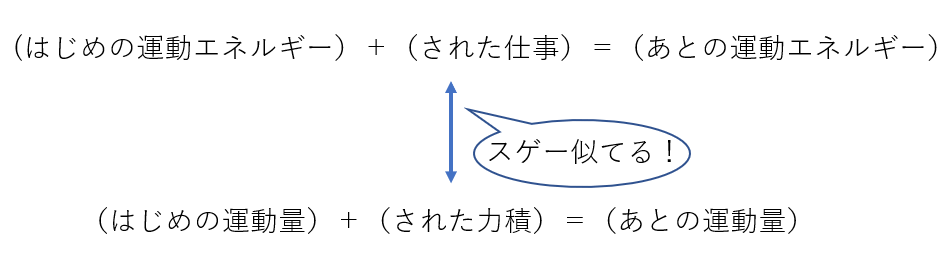
この二つは関連付けて覚えておくと良いですね。
(エネルギー保存則について詳しく知りたい方はこちらを確認ください)
力積はグラフからも求められる

ここでちょっと力積について注意点があります。
さっき、力積は\(\vec{F}\Delta t\)という風に「力×時間」と表せるよ!って言いました。
ただ、これには条件があります。
力が一定のとき
です。
じゃあ、力が一定じゃないときは?
というと、F-tグラフ(力と時間のグラフ)の面積で求められます。
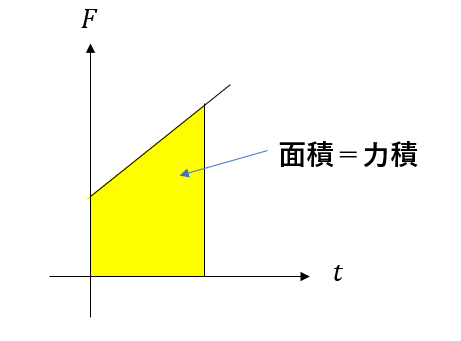
仕事も同じような注意点がありましたね。なのでこの性質もかなり似ていますね。
運動量保存則2:力学的エネルギー保存則とそっくり!?

あ!もしかして、運動量保存則もエネルギー保存則と同じ感じでは!?
 AI
AI
お!いいところに気づいたね。そうなりそうだね。実際に確かめてみようか
 AKINORI
AKINORI
質量がそれぞれ\(m_1, m_2\)である二つの物体がそれぞれ\(\vec{v_1} , \vec{v_2}\)の速度で衝突する。衝突後、物体の速度がそれぞれ\(\vec{v_1′}, \vec{v_2′}\)となったとき、運動量の関係を考えよ。

さっきの運動量と力積の関係を使ってみよう。
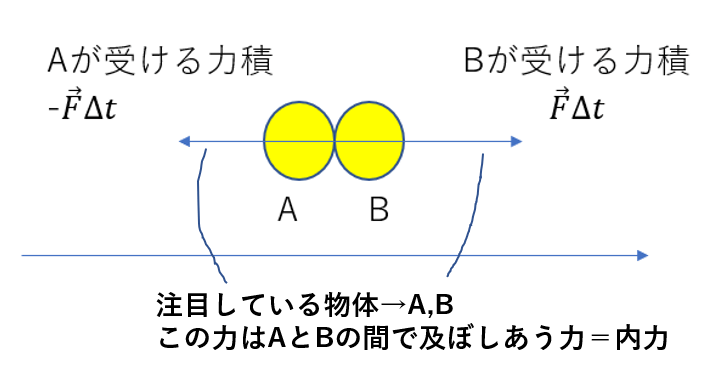
まず、衝突する瞬間を図に表してみよう。
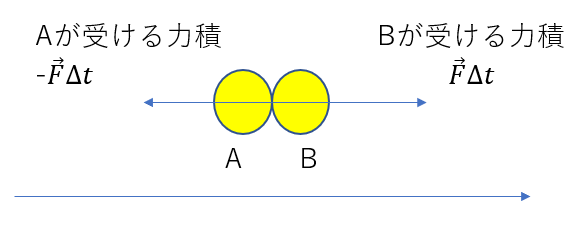
Bが受ける力積を\(\vec{F}\Delta t\)とすると、作用反作用の法則から、
Aが受ける力積は\(-\vec{F}\Delta t\)となります。
これを踏まえて、それぞれの物体について運動量と力積の関係を考えると
A:\(m_1\vec{v_1} + (-\vec{F}\Delta t) = m_1\vec{v_1′}\)
B:\(m_2\vec{v_2} + \vec{F}\Delta t = m_2\vec{v_2′}\)
この二式を見たら足したくなりますね!
なので、足します。
\(m_1\vec{v_1} + m_2\vec{v_2} = m_1\vec{v_1′} + m_2\vec{v_2′}\)
この式をじっくり眺めてみるとこんなことが言えますね。
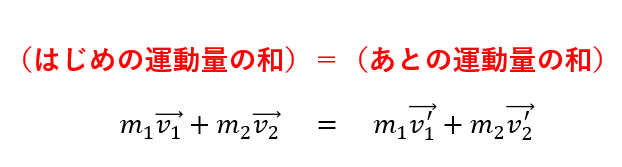
かなりきれいな関係ですよね。これがいわゆる「運動量保存則」です。
「衝突前後の運動量の和は一定」
と言葉に置き換えることができます。
内力のみはたらく場合に限る
しかし、これはある条件でのみ成り立ちます。
それが内力のみはたらく場合です。
内力とは「物体同士で及ぼしあう力」のことです。
つまり、
「注目している物体同士で作用反作用が完結している」
ときこの関係式が成り立つわけです。
なんか条件といい、式の形といい、力学的エネルギー保存則と似てる!!
 AI
AI
そうだね。これも力学的エネルギー保存則と関連づけられるね。
 AKINORI
AKINORI

このように関連付けてもいいですね。
ちなみに、先ほど僕はいわゆる「運動量保存則」と言いました。
これは教科書ではこういわれているからなのですが、実はこれが本当の意味では運動量保存則ではないんです。
エネルギー保存則でも、上のようないわゆる「力学的エネルギー保存則」は覚える必要はないと僕は教えています。
同じように上の運動量保存則も覚える必要は全くなく、より広く使える真の運動量保存則があります。
それを今から学んでいきましょう。
運動量保存則3:真の運動量保存則とは?

次は外力がはたらく場合も考えたいですよね。これもやっぱり・・・
 AI
AI
鋭い!!やっぱり、エネルギーと似るんでしょうね。実際に考えてみよう
 AKINORI
AKINORI
図のように、質量\(m_1 , m_2\)の二つの物体がある。この二つの物体はそれぞれ一定の力\(\vec{F_1}, \vec{F_2}\)を受けている。はじめ\(\vec{v_1}, \vec{v_2}\)の速度を持っていて、時間\(\Delta t’\)後に\(\vec{v_1′} , \vec{v_2′}\)の速度に変化した。この物体は\(\Delta t’\)の間に一度だけ衝突するとして、運動量の変化について考えよ。
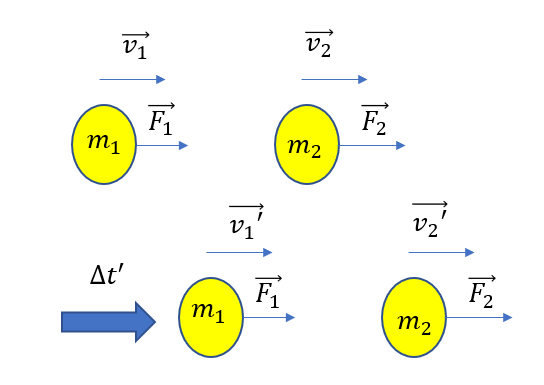
さっきと全く同じように運動量と力積の関係を使ってみましょう。
まずは、衝突の瞬間を考えると、これはさっきやった場合と全く同じです。

ということで、
(はじめの運動量)+(された力積)=(あとの運動量)
A:\(m_1\vec{v_1} + \vec{F_1}\Delta t’ + (-\vec{F}\Delta t) = m_1\vec{v_1}\)
B:\(m_2\vec{v_2} + \vec{F_2}\Delta t’ + \vec{F}\Delta t = m_2\vec{v_2}\)
もちろん、両辺足したくなりますね。
足してみると・・・
\(m_1\vec{v_1} + m_2\vec{v_2} + \vec{F_1}\Delta t’ + \vec{F_2}\Delta t’ \)
\( = m_1\vec{v_1′} + m_2\vec{v_2′}\)
もう想像通りの結果だと思います。
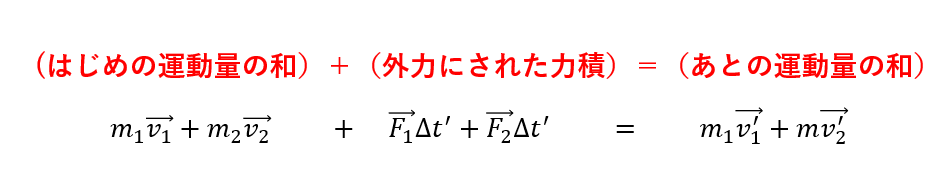
「仕事をされればエネルギーは変化する」というのが仕事とエネルギーの本質であるなら
「力積を受ければ運動量は変化する」というのが運動量の本質なのです。
そして、外力が働かなければ、「(外力にされた力積)=0」なのでこれはさっきみた運動量保存則になりますね。
なので覚える必要がなかったのです。
やっぱり。エネルギー保存則とほとんど同じですね。
 AI
AI
そうだね。最後にエネルギーと運動量の関連を見て終わりにしよう。
 AKINORI
AKINORI

運動量保存則をどのように使い分けるの?
このように形がそっくりなのもありますし、運動量とエネルギーの違いもいまいちピンとこない人も多く
使い分けに困ってしまうことがよくあります。
なのでここで簡単に、どのように使い分けるかを教えていきます。
運動量は2物体の衝突に使えて「向き」が大事です
まず運動量ですが、先ほど見てきたように2物体の運動を考えるときに力を発揮します。
また「ベクトルの関係式」というのもあって、向きという情報が加わってきます。
エネルギーは1物体の運動、あるいは2物体で衝突が無い場合に使えます
一方で、エネルギーは基本的に1つの物体に関して考えます。
もちろん2物体でも使えますが、あくまで衝突が無い場合につかうことがほとんどです。
実は衝突が起こってしまうと、熱や音のエネルギーに変わってしまって、エネルギー保存則が使えないからです。
(例外はあるので詳しくは別の記事で)
以上を踏まえて使い分けできるといいでしょう。
運動量保存則とエネルギー保存則はなんで似てるの?

最後に少し補足としてお話します。
この2式がそもそも似ている理由、気になりすよね?
実はこれらは両方とも運動方程式から導いたものです。
さらには一方の式からもう一方の式を導くこともできます。
なので似てて当然なのです。
先ほどの運動量と力積の関係を見てください。(今回、速度をプラスマイナスをつけた速さで表します)
これを\(t\)で微分してみますね。
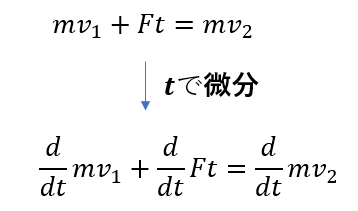
この状態で両辺に\(v\)をかけてみます。
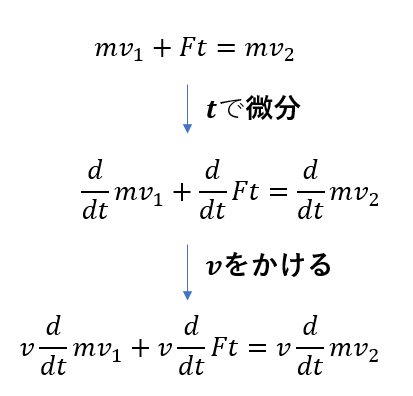
さて、実はそれぞれをきれいにすることができます。

ということで整理すると次のようになります。
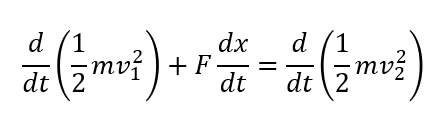
結局これを\(t\)で積分すると、\(\frac{1}{2}mv^2\)や\(x\)がそのまま表れます。
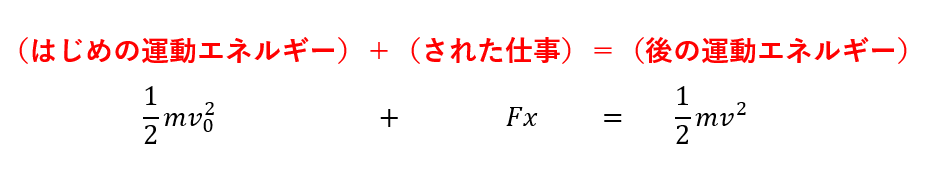
このように、運動量保存則からエネルギー保存則が導けました。
なので、式として似ていて当然なわけです。
この話は覚えなくていいです。「そういうことなんだなあ、ふ~ん」程度でOKです。
まとめ:運動量保存則とエネルギー保存則は関連させて覚えよ

いかがでしたか
運動量保存則とエネルギー保存則は非常に似ているので関連付けて覚えちゃいましょう。
ただし、似ているのは式だけの話で、運動量とエネルギーは全く別の概念です。今回少し教えたように、使い道も大きく変わっています。
なので、その違いも踏まえて理解しておきましょう。

運動量は2物体の衝突に使えて「向き」が大事です
まず運動量ですが、先ほど見てきたように2物体の運動を考えるときに力を発揮します。
また「ベクトルの関係式」というのもあって、向きという情報が加わってきます。
エネルギーは1物体の運動、あるいは2物体で衝突が無い場合に使えます
一方で、エネルギーは基本的に1つの物体に関して考えます。
もちろん2物体でも使えますが、あくまで衝突が無い場合につかうことがほとんどです。
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!








