【融合問題】極板間引力の単振動。融合されてもやるべきこと１つ！
Akinoriさん。極板間引力について考えたじゃないですか？あれから発展して何か問題で出ますか？
AI
うん。これと単振動を組み合わせたりして入試問題でも出たりするよ。こういう融合問題は入試で多く出てくるからしっかり対応できるようにしましょう。
AKINORI
極板間引力の単振動。
実際に入試問題で出たことがあります。（横浜国大とか）
このように「力学」と「電磁気学」を融合する問題も多く出てきます。
その時も、しっかり段取りを決めて解く。一個一個考えて解く。
融合されても対応できる力をここで鍛え上げましょう！
極板の単振動
真空中に二枚の金属板を向い合せたコンデンサーを作る。極板Bは固定されていて、極板Aはばね定数\(kの\)ばねに取り付けられている。Aの質量は\(m\)であり、ここでは重力を無視して考える。
まず、Aを固定し、電圧\(V\)の電池でコンデンサーを充電した。この時、極板間の距離は\(d\), 電気容量は\(C\)である。充電後、電池は取り外し、Aの固定を外したとき、Aの運動について考える。ただし、ばねが自然長の時のAの位置を原点に取り、右向きを正にする。
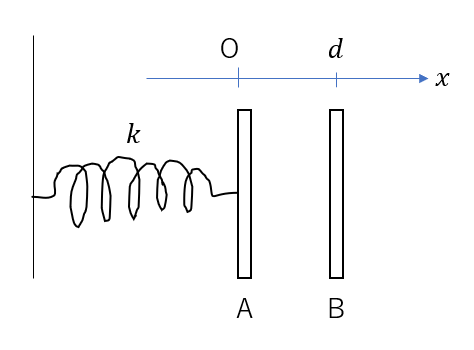
(1) 極板間引力の大きさ\(F\)を求めよ。
(2) Aが単振動することを示し、振幅と周期を求めよ
(3) AがBに最も近づくときのAの位置を求めよ
（１）極板間引力は・・・
あ！これやったやつです！「電場」か「エネルギー」のどちらかの立場で考えることができたんですよね。
AI
極板間引力の詳しい説明についてはこちらをチェックしてください！
この記事によれば
\(F = \frac{1}{2}QE\)
ですよね。
\(Q = CV\)と\(V = Ed\)を使えば
\(F = \frac{CV^2}{2d}\)
となります。
もちろん、この値は一定です。
（２）単振動は\(a = – (定数)\times (xの一次式)\)
ここは「単振動」なので、流れが決まってましたね！
AI
単振動では絶対に踏んでほしいステップがありました。
それについてはこちらで説明しています！！
まずは、運動方程式を立てていきますね。
軸はすでに定まっています。
もし自分で設定する場合は、自然長を原点にとってくださいね。
単振動ではベクトルを使わないと混乱します。
ベクトルで力を成分表示して表す。
のですが、弾性力が厄介ですね。向きが位置によって変わっちゃうから。
なので、場合分けです。
- ばねが伸びたとき
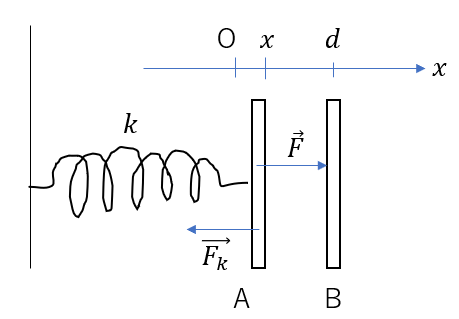
ばねが伸びると
- 位置座標 \(x > 0\)
- 弾性力の向きは左→成分は負
\(\vec{F_k} = (〇)\)の形にするときに（）の中は負でないといけません。
\(\vec{F_k} = (-kx)\)
となりますね。
- ばねが縮んだ時
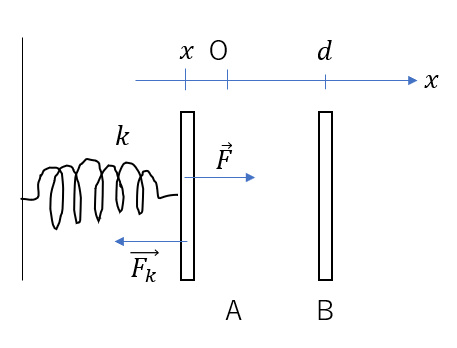
この時は
- 位置座標\(x < 0\)
- ばねの向きは右→成分は正
この場合も、やはり
\(\vec{F_k} = (-kx)\)
になりますね。
つまり、どの位置にいても
\(\vec{F_k} = (-kx)\)
が成立するわけです。
もちろん、極板間引力は右向き一定です。
つまり
\(\vec{F} = (F)\)
です。
そして合力を求めます。
とにかくベクトルで足すんでしたね！
\(\vec{F_s} = \vec{F_k} + \vec{F} = (-kx + F)\)
あとは運動方程式を使うだけ。
\(m\vec{a} = \vec{F_s}\)
\(ma = -kx + \frac{CV^2}{2d}\)
\(a = -\frac{k}{m} (x – \frac{CV^2}{2kd}\)
\(a = – (定数)\times (xの一次式)\)になりましたね。
AI
なので、単振動するってことが分かりますね。そして、単振動と分かったときにやるべきこと３つを忘れずに
AKINORI
単振動と分かったときにやるべきことは・・・
１ 振動の中心を求める
これは\(a = 0\)とすれば良くて、中心\(x_0\)は
\(x_0 = \frac{CV^2}{2kd}\)
です。
これが振幅になります。
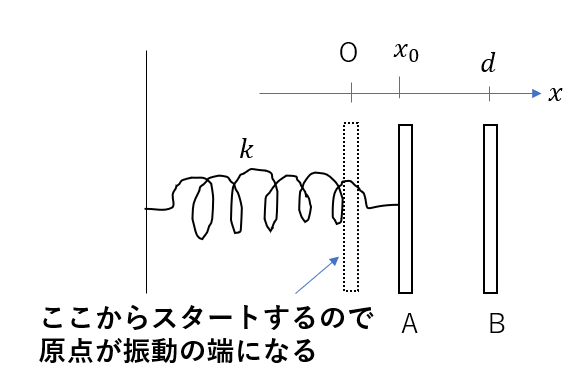
このように原点でスタートするので、ここが振動の端になります。
ここは原点なので、そこから中心までの距離がまさに振幅となるわけです。
２ \(\omega\)を求める
これは\(\omega = \sqrt{定数}\)と表せたので
\(\omega = \sqrt{\frac{k}{m}}\)
ですね
３ 周期\(T\)を求める
周期は\(T = \frac{2\pi}{\omega}\)
と求められるので
\(T = 2\pi \sqrt{\frac{m}{k}}\)
ですね。
周期はこれが答えです。
しっかり単振動のステップが踏めていれば大したことない問題ですね。
（３）反対の振動の端をみつけておしまい！
Bにもっとも近づくっていうのは・・・振動の端に来た時ですね！
AI
そうだね。もう簡単だね。
AKINORI
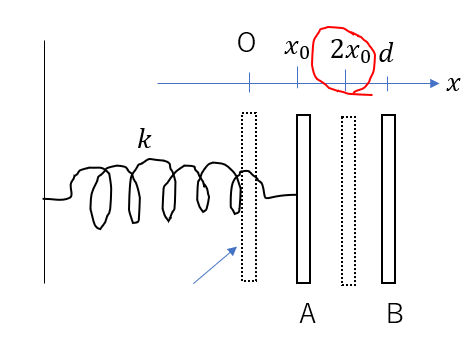
振幅が\(x_0\)っていうのがわかっているので、逆側の振動の端は
中心から\(x_0\)だけ進んだところにありますよね。
それは位置でいうと
\(2x_0\)
です。
ということで求める位置は
\(x = 2x_0 = \frac{CV^2}{kd}\)
はい、おしまいです。
融合問題も一つ一つ見ていけば大したことないですね。
AI
そうだね。結局は単振動だから、やることも一緒だよね。「電磁気」という分野に惑わされて、単振動の流れをおろそかにしちゃだめだよ！
AKINORI
それでは！！
こんな問題もチャレンジ！！
