【高校物理】全反射はなぜ起こる?光ファイバーの問題でチェック

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
今回は全反射について話をしていきたいと思います。
最初に言っておくと全反射は全く覚える必要がありません!
全反射は屈折の法則の延長にあるので、屈折の法則さえ分かっていればOKです。
とはいえ、原理を知っておく必要はあります。
今回は、全反射がどういう現象でなぜ起こるのかを分かりやすく説明します。
最後に、全反射の典型である光ファイバーの問題も解説していきます!
全反射の原理は屈折の法則で導ける!
目次
全反射とは?
二つの媒質を光りが通過するとき、境界面で屈折が起こります。

屈折率が小さいほうから大きいほうへ進行するとき、入射角を大きくしていくと屈折光はどんどん境界面に近づいていきます。
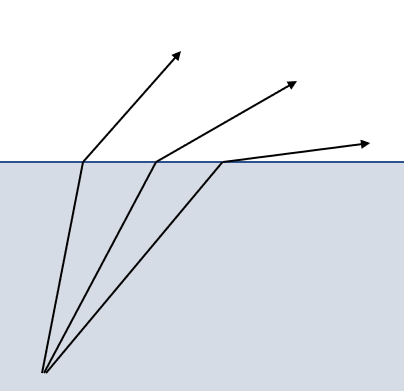
そして、入射角がある大きさになると、光は境界を越えることができなくなり、すべての光が反射されます。この現象が全反射です。
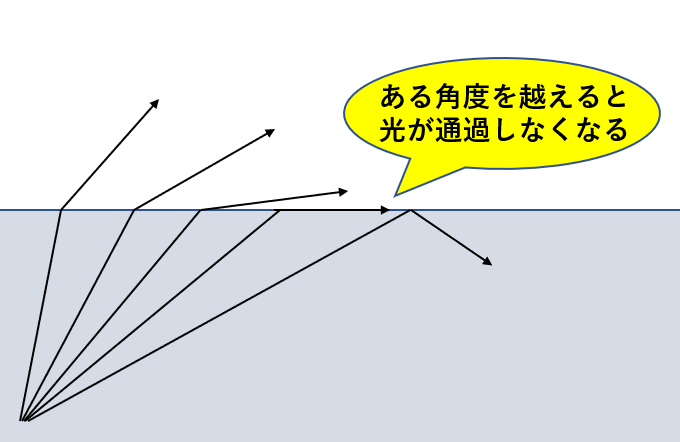
全反射が起こる条件と理由
なんで入射角を大きくすると境界に近づいて全反射するんですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
これは屈折の法則を考えると理解できるよ
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
全反射は常に起こるのではなく、ある条件があります。
屈折率が小さいほうから大きいほうへ進行するとき、全反射が起こります。
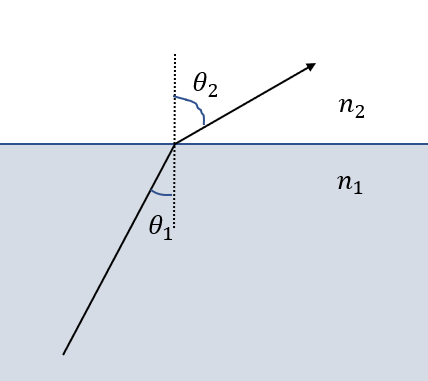
図のように、屈折率\(n_1, n_2 (n_1 > n_2)\)の媒質を通過する光があって、入射角を\(\theta_1\)、屈折角を\(\theta_2\)とすると、屈折の法則より次の式が得られますね。
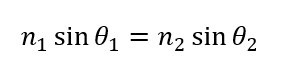
\(n_1 > n_2\)なので\(\frac{n_1}{n_3} > 1\)となります。この条件から、\(\theta_1, \theta_2\)の大小関係を求めることができます。

入射角と屈折角は90°を越えることは無いので、sinの大小関係がこのようになれば、角度の大小関係も同じようになります
\(\theta_2 > \theta_1\)
つまり、入射角よりも屈折角の方が大きくなり入射角を大きくしていくと水平面に近づいていくのです
そして、ある角度を越えると全反射します。
全反射の角度(臨界角)を屈折の法則から導く
では、全反射が起こる瞬間の入射角はどれくらいになるか?
これを求めてみましょう。先ほどのと同じように屈折の法則を使えば求められます。
これまで見てきたように、全反射は屈折光が境界面に沿ったところ以降で起こります。
ですから、この境界面に沿う場合を考えればOKです。
境界面に沿うということは、屈折角が90°になるということです。
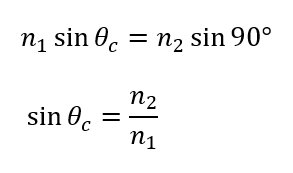
入射角がこのように、屈折率の比できれいに表すことができました。
この、全反射が起こる瞬間の入射角\(\theta_c\)を臨界角と言います。
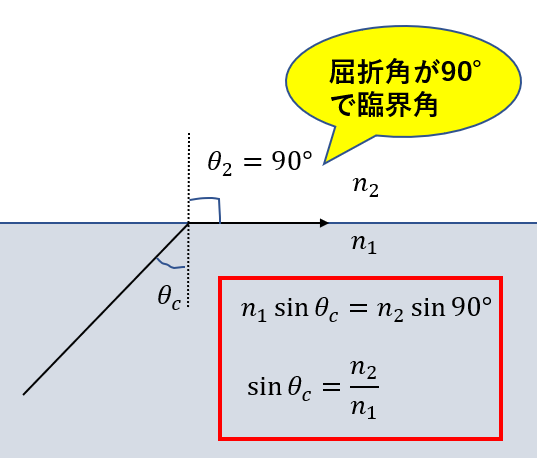
臨界角の式は覚える必要はない
ここまで見て分かったと思いますが、何も特別なことをしていませんよね?
ただただ屈折の法則を使ったら全反射という現象を考えることができただけです。
臨界角の式を求めましたが、こんなのは全く覚える必要ありません。
大事なのは、「全反射するときは屈折角が90°になって、屈折の法則を使う」ということです。
常にこの方法で全反射は考えてください。
全反射はどのように利用される?
この全反射は日常生活でも応用されていて、その例が光ファイバーです。
光ファイバーは光を伝える必要がありますが、普通であれば透過してしまうので途中で光が伝わらなくなります。
しかし、管の中で全反射を繰り返し行わせることで途中で透過することなく光を伝えることができます。
ということで、光ファイバーの原理を問題として見ていきましょう
全反射の問題:光ファイバー
屈折率1.5の平面ガラス版の上下を、屈折率\(n (n < 1.5)\)の媒質で挟み、左端A、右端Bの外側は真空とする。この平面ガラスの端Aから、入射角\(\theta\)で光が紙面に平行に入射した。
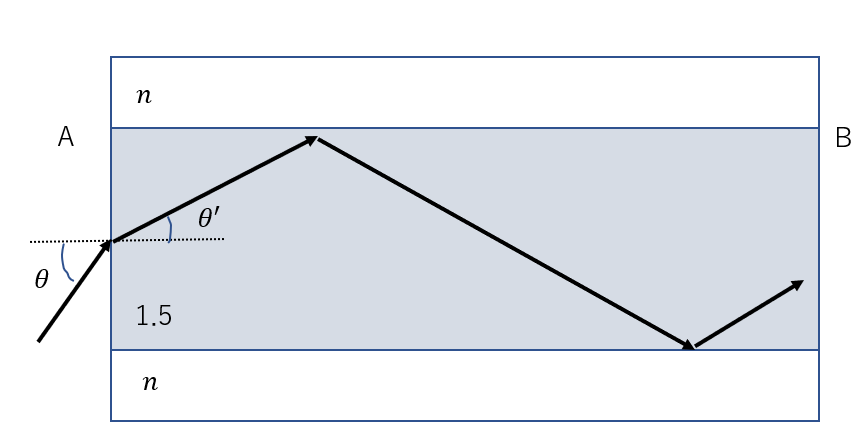
(1) 入射角\(\theta\)でガラス版に入射したときに屈折角\(\theta’\)を求めよ
(2) (1)の状況で光が上下の境界面で全反射される条件を\(\theta’\)を用いて求めよ
(3) 入射した光が上下の境界面で全反射される条件は、\(\sin{\theta}\)がいくら以下のときか求めよ
(4) \(\theta\)に依らず、入射した光が上下の境界面で全反射される条件は\(n\)がいくら以下のときか求めよ
(セミナー物理2016 問405)
全反射の問題解説1:屈折の法則を使いこなそう
(1)は屈折の法則そのものですね。特に解説するところはありません。
ちなみに特に断りがない場合、真空(空気)の屈折率は1でOKです。

全反射の問題解説2:全反射する瞬間は屈折率が90°
全反射の条件なので、臨界点を求めればOKです。これは臨界点を考えばOKです。
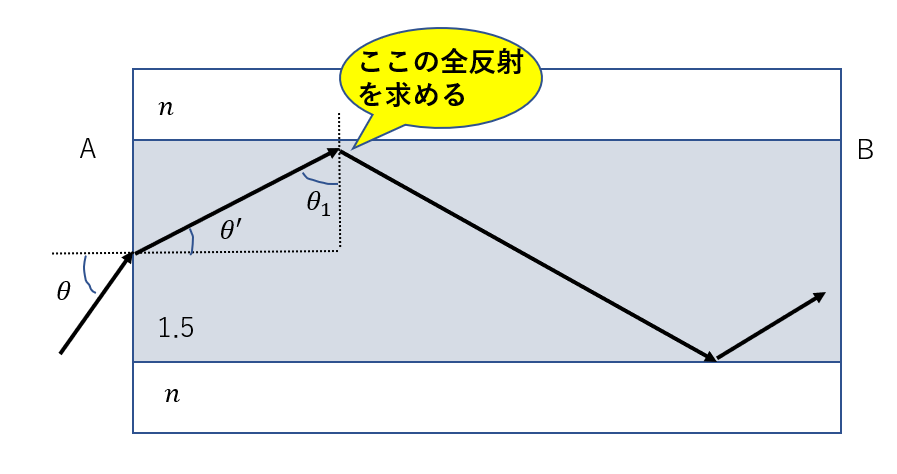
全反射する条件を求めますが、まずは臨界角を求めるべきですね。
臨界角は屈折率が90°として求めることができます。
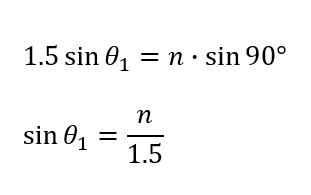
このときが全反射する瞬間なので、\(\theta_1\)がこれより多きくなる、つまり\(\sin{\theta_1}\)が\(\frac{n}{1.5}\)より大きくなれば全反射します。
ただし、\(\theta’\)で求めないといけませんので、置き換えます。
図のように三角形を考えれば\(\theta_1\)を書き換えられます。
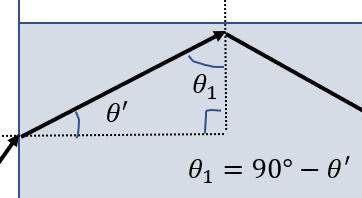
ということで条件式を求めることができます。
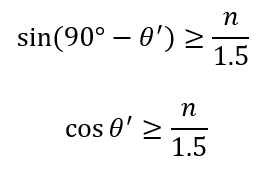
全反射の問題解説3:sinとcosの関係をうまく使おう
(3)は(2)の式からさらに変形して、\(\theta\)の条件として表します。
\(\theta, \theta’\)の関係は(1)で求めていますが、これはsinの式で表されているのでうまくcosに変換する必要があります。
数学をやっているみなさんならできますよね。
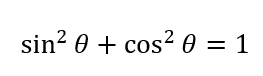
これを使えばOKですね。
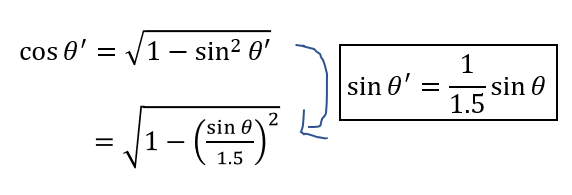
あとは先ほどの不等式から\(\sin{\theta}\)の条件式にもっていけばOKです。

全反射の問題解説4:sinの取り得る範囲を考える
(4)は(3)の結果に別の条件式をうまく当てはめる必要があります。
\(0 < \theta < 90^\circ\)なので\(0 < \sin{\theta} < 1\)ですね。
そしてこの問いでは、「どんな\(\theta\)にしても(2)の条件が成り立つようにしろ」という意味です。
sinが0から1までの範囲しか取らないのであれば、\(\sqrt{1.5^2 – n^2}\)が1以上であれば良いということですね。

あとはこれを式にして、\(n\)の条件を求めれば終わりです。
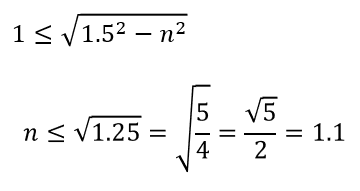
つまり、外側の媒質の屈折率を調整することで、どのように光が照射しても端から端まで光を伝えることができるのです。これが光ファイバーの原理です。
まとめ:全反射は屈折の法則の特別バージョン
いかがでしたか?
全反射は屈折の法則から分かる現象で、臨界角も屈折の法則から導かれる、ただそれだけのことです。
ですから、「全反射だからこう」のように暗記するのではなく、屈折の法則を使った延長として全反射があるんだなぁという感覚で理解をしてほしいと思います。
全反射の臨界角
→常に屈折の法則から導け!
→屈折角が90°のときの入射角










Comment
条件のところ屈折率が大きいほうから小さいほうですよ!