投げ上げ・落下運動の公式【自由落下や斜方投射の場合分けは不要】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
物理基礎の自由落下や斜方投射などの落下運動や投げ上げ運動の公式が覚えられません…
 リケジョになりたいAIさん
リケジョになりたいAIさん
今回はこんな悩みを解決していきます。
結論から言うと、「自由落下だからこう」「斜方投射だからこう」のように場合分けして公式を覚える必要はありません。
覚えるべき公式はたった3つです。
これが分かるだけで、暗記量をググっと減らし、かつ応用問題も問題なく解けるようになります。
目次
落下運動と投げ上げ運動とは?
物理基礎で「落下運動」「投げ運動」学びます。
主に5つの運動が例として出されていますね。
- 自由落下
- 鉛直投げおろし
- 鉛直投げ上げ
- 水平投射
- 斜方投射
物理基礎の最初の壁がこの単元です。
覚えるべきは等加速度直線運動の公式3つだけ!
教科書などを見ると、「自由落下の公式」のように運動ごとに公式を紹介していることがあります。

これを暗記させられたり
「\(g\)を\(-g\)に変えれば良いですよ」とか「\(v_0\)を\(0\)とすれば良いですよ」とか言われたり
これが結構ヤバいんですね。
こんなのは覚える必要は全くありません。
落下運動や投げ上げ運動は等加速度運動でしかありません!
等加速度運動の公式の使い方が分かればOK
等加速度運動であるなら等加速度運動の公式さえ覚えていれば自由落下の式とかいちいち場合分けする必要なんてないんです。
等加速度運動の公式とその使い方を正しく知っていればいいのです。
しかし、多くの高校生は正しい知識と使い方を知りません。
ですから、今ここで理解してください。
等加速度運動の公式
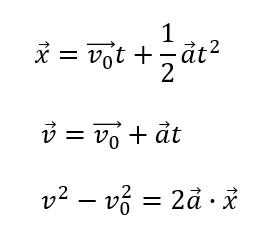
等加速度運動の公式の使い方
・軸を取る
・ベクトルを成分表示して、成分を代入
これさえ知っていれば落下運動と投げ上げ運動は攻略したも同然です。
この3つの公式と使い方だけを理解してください
これを踏まえて4つの運動を具体的に見ていきたいと思います。
等加速度運動の公式については以下の記事で詳しく解説しているのでぜひ読んでください
自由落下の公式
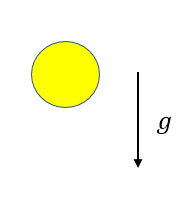
自由落下は「ゆっくり手を放して落とす」運動です。
加速度は下向きに大きさ\(g\)なので等加速度運動なので先ほどの公式が使えます。
等加速度運動の公式は「ベクトル」で表されているので、軸を取って成分表示(\(\pm 大きさ\)の形)で表さなければいけません。
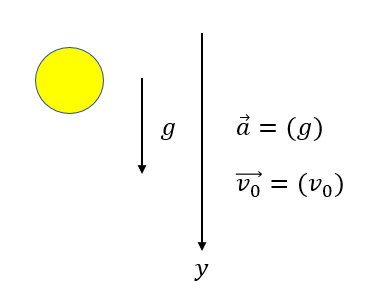
軸は好きな向きにとっていいので、今回は下向きに取ります。
すると、加速度の向きは軸に一致するので\(\vec{a}=(+g)\)と表せます。
また初速はないので\(\vec{v_0}=0\)ですね。
あとはこれを式に代入すればいいだけです。
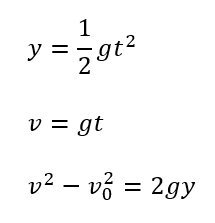
簡単ですね。
鉛直投げ上げの公式

鉛直投げ上げは「鉛直上向きに初速を与えて放り投げる運動」です。
これも等加速度運動なので、同じように軸を取って、ベクトルの成分表示をします。
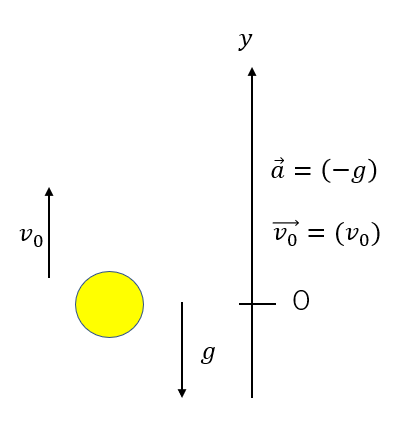
今回は上向きに軸と取ってみました。
加速度は軸と逆向きになるので\(\vec{a} = (-g)\)と()の中身をマイナスにします。
初速度は向きが一致しているので\(\vec{v_0}=(v_0)\)です。
あとは公式に代入すればOKです。
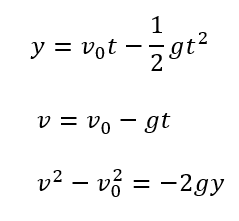
やはり教科書に載っている式が導けました。
特別なことはやっていません。
等加速度運動の公式の使い方通りにやっただけです。
水平投射の公式
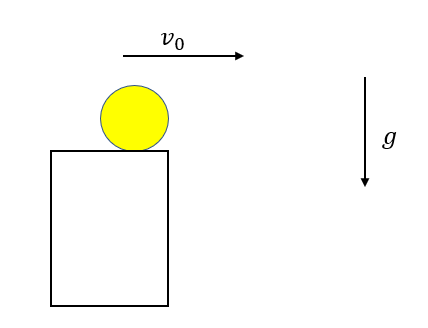
水平投射はある高さから水平に飛ばしたときの運動です。
これは前の2つの場合と違い、直線運動ではありません。
このように場合は運動の方向を分け(つまり軸を2つ取り)それぞれで考えます。
水平投射の水平方向の運動
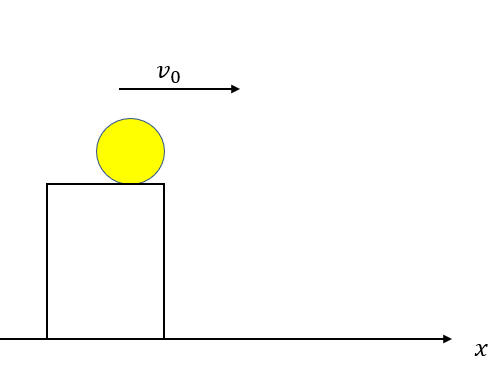
水平方向は図のように軸を右向きに取った場合
加速度は水平方向に生じていないので0です。
初速度は軸と同じ向きなので\(\vec{v_0}=(v_0)\)となります。
後は等加速度運動の公式を使えばOKです。
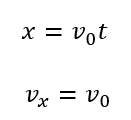
水平投射の鉛直方向の運動
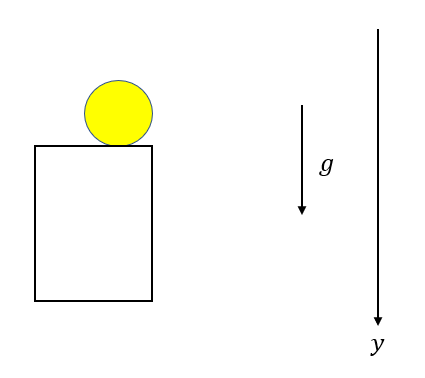
鉛直方向は下向きに軸を取ってみます。
加速度は軸の向きと同じなので\(\vec{a}=(g)\)です。
水平に初速度を与えたので、鉛直方向には初速度は0です。
これは自由落下と同じですね。
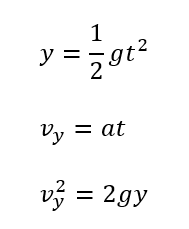
斜方投射の公式
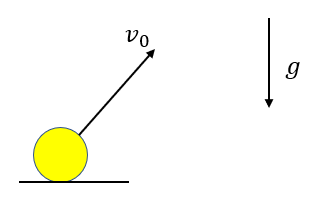
斜方投射は水平面からある角度の方向に投げる運動のことです。
もう慣れてきたと思いますが、最後も確認しましょう。
今回も2つの方向に分ける必要がありますね。
斜方投射の水平方向の運動
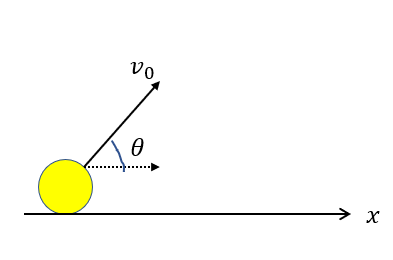
右向きに軸を取りましょう。
まず加速度は水平方向には生じていないので0です。
初速度は図のように水平面からも角度を\(\theta\)とすると、初速度の大きさは\(v_0\cos{\theta}\)と表せます。
向きは軸と同じ向きなので\(\vec{v_0} = (v_0 \cos{\theta})\)です。
(初速がsinかcosはどこの角度を使うかでもちろん変わります。たまに、水平方向は必ずcosとなるという誤解をする人がいます)
あとはこれを公式に当てはめるだけです。
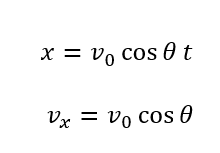
斜方投射の鉛直方向の運動
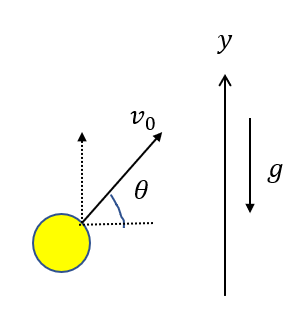
軸を鉛直上向きに取りましょう。
加速度は軸の向きと逆向きなので\(\vec{a}=(-g)\)です。
初速度ですが、大きさは\(v_0\sin{\theta}\)ですね。
向きは軸と同じ向きなので、\(\vec{v_0} = (v_0 \sin{\theta})\)となります。
これらを公式に当てはめます。
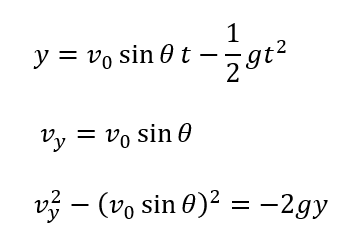
このように、投げ上げ運動のよな直線運動ではない場合は運動の方向を分けて考えることでうまくいきます。
運動方向を分ける場合は状況に合わせる
今回の水平投射や斜方投射は水平・鉛直で分けていましたが、これが絶対ではありません。
問題の状況に合わせて簡単になるように分けるべきです。
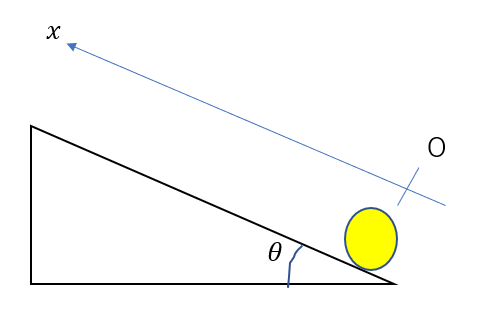
例えば、斜面上を動く運動であれば、台に沿って水平・垂直に分けた方が分かりやすいですね。
軸の取り方次第でいくらでも式は変わる
学校では「\(g\)を\(-g\)に変えれば鉛直投げ上げになりますよ」のように教わった人もいるかと思います。
ですが、これは必ずしもそうではありません。
等加速度運動の公式は軸の取り方が重要なのです。
例えば、鉛直投げ上げで下向きに軸を取ってみるとどうでしょう?
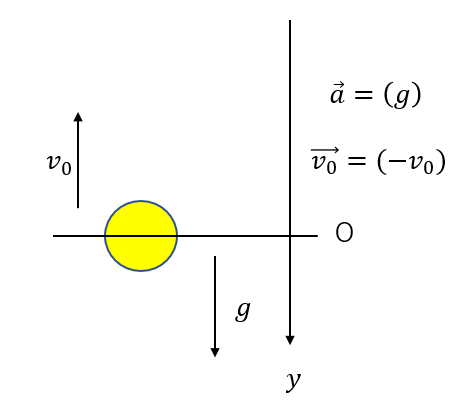
加速度は軸と同じ向きになるので\(\vec{a}=(g)\)となります。
初速度は軸と逆向きになるので\(\vec{v_0}=(-v_0)\)となります。
後は式に代入します。
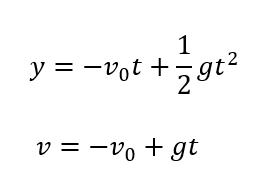
これも立派な鉛直投げ上げの式です。
\(g\)を\(-g\)にすれば公式が得られるというわけではないんですね。
先ほどの場合とこの場合では、求めたい\(y\)や\(v\)の符号が逆で現れます。
それは求めたいものは「軸の向きに取っておく」という決まりがあるからです。
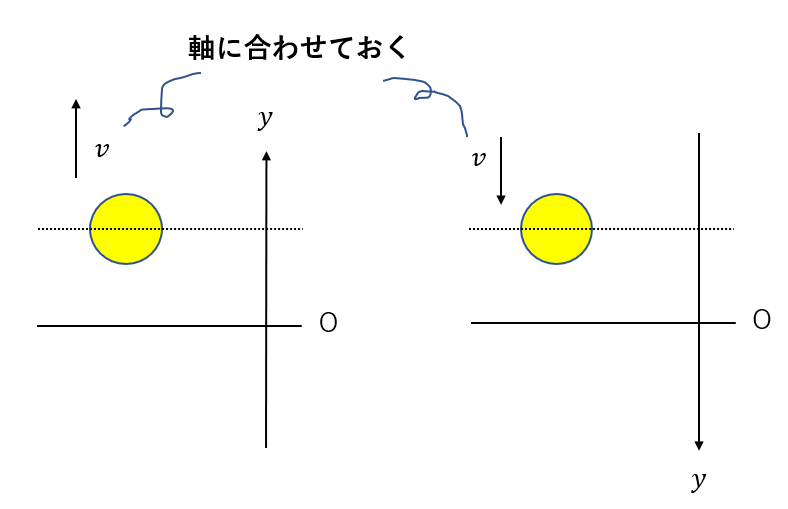
いずれにしても、最終的に出た答えがプラスマイナスかで向きが決まるので、答えは一致します。
とにかく軸によって式がガラッと変わるということを理解してください。
まとめ:等加速度直線運動の公式がすべて
いかがでしたか?
落下運動などの公式を場合分けするのはバカらしいと分かりましたね。
等加速度運動の公式とその使い方をしっかり理解しておけば問題ありません。
それでは、しっかり復習して問題演習しましょう!!
落下運動や投げ上げ運動の公式は覚えるな!
→等加速度運動の公式とその使い方を学べ!










