交流回路解説!RLC直流回路のインピーダンスとは?

交流回路問題の解き方が分かる
抵抗・コンデンサー・コイルの扱いが分かる
RLC直列回路について分かる
インピーダンスの意味が分かる
こんにちは。教科書や問題集ではとにかく説明を省いているのがこの交流回路です。
RLC直列回路とかインピーダンスとか急に出てきて意味わからず混乱する人って本当に多いんですよね。
対策も不十分で入試でまさかの交流回路が出てきて見事に0点
・・・なんていうことが起こらないようにここでしっかり学習しておきましょう。
交流回路でも直流回路と同じことをやります。キルヒホッフの法則が基本です。そこに交流特有の特徴を学んでいけばOKです。
抵抗・コイル・コンデンサーを直列につなぐ
図のように3つの素子を直列につなだとき、電源の電圧を式で表そう
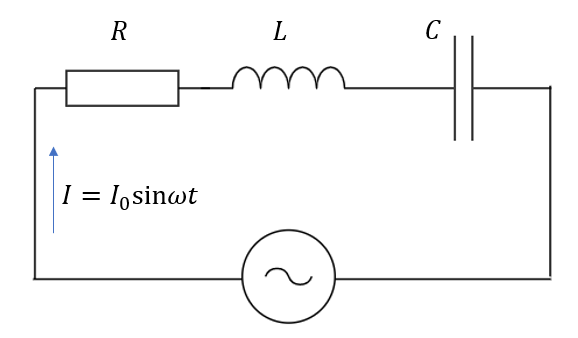
なんでこんなことやるかと言いますと、直列のときを思い出してください。
合成抵抗なんてものやりませんでしたか?
合成抵抗というのは複数の抵抗を一つの抵抗に置き換えることです。直流でそれができたというなら交流でもできますよね?
つまり、交流における合成抵抗を考えるのがこの章の意味になります。
交流の抵抗と言えばリアクタンスだ!
 AI
AI
交流回路における3つの素子の性質はすでに学んでいますね。(わからない人はこのページの最初に紹介した記事をみてください)
そしてコイルとコンデンサーも実は抵抗と同じ役割を果たすという話も知っていますね。
ですから合成もおそらく可能なわけです。それをここで考えていこうというわけです。
ただあくまで交流なので単純に足したり、逆数の和を取ったりするのではうまくいきませんのでご注意を。
各素子の電位差は?

いつもは電源の電圧が式で与えられていますが今回は電流が式で与えられています。というのも直列なら電流はどの素子にも同じ値で流れるからです。
そして目標はもちろん\(V = RI\)の形です。なので、電流の式から3つの素子にかかる電圧の合計、つまり電源の電圧を求めてやりましょう。
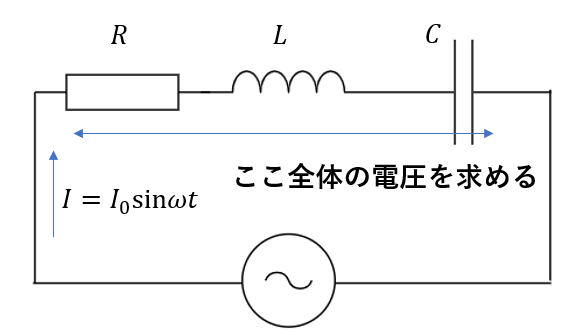
もちろん、キルヒホッフの法則の法則ですね。「一周した電位=0」です。
まずは各電位差を導いていきます。
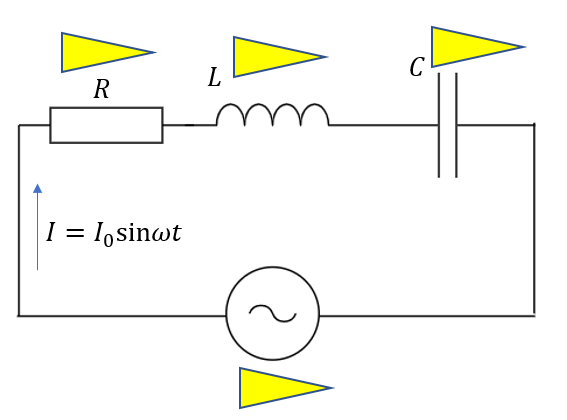
- 抵抗
これは\(V = RI\)から分かりますね。
\(V_R = RI_0\sin{\omega t}\)
- コイル
コイルには特徴がありましたね。位相です。コイルに関する電流と電圧には位相差が生まれているんでした。
こちらの記事では「電流は電圧より位相が\(\frac{\pi}{2}\)遅れる」と表現していました。
つまり「電圧は電流より位相が\(\frac{\pi}{2}\)進む」です。
今回は電流の式が分かっていて電圧を求めないといけませんからこう考えないといけないのですね。
また、コイルでも\(V = RI\)の関係が成り立つことも別記事で説明しています。この時の\(R\)は\(R = \omega L\)でしたね。
ということで式にこれらをまとめると
\(V_L = \omega L I_0 \sin{(\omega t + \frac{\pi}{2})}\)
\(V_L = \omega LI_0\cos{\omega t}\)
となります。
- コンデンサー
こちらもコイルとほぼ同じです。詳しくはこちらを参考にしてください。
まず位相についてですが、その記事では「電流は電圧より位相が\(\frac{\pi}{2}\)進む」と表現しています。
これは「電圧は電圧より位相が\(\frac{\pi}{2}\)遅れる」ですね。
また、コイルと同じように\(V = RI\)が成立して、この時の\(R\)は\(R = \frac{1}{\omega C}\)です。
ということで整理すると
\(V_C = \frac{1}{\omega C}・I_0\sin{(\omega t -\frac{\pi}{2})} = -\frac{1}{\omega C}I_0\cos{\omega t}\)
ということですね。
コンデンサーにはマイナスが付いているので電圧マークの向きが逆になるように思えますが、直流と違い時間的に変化するので電圧マークの向きもそれにともなって変わっていきます。
このように時間的に変化する場合は、電圧マークの向きを最初に決めておいて特に向きを変えたりせずそのまま計算していきます。式が向きの考慮をしてくれているので大丈夫です。
全体の電圧を求めよう

後は一周してやればいいです。
「一周した電位=0」なので
\(V – V_R – V_L – V_C = 0\)
\(V = V_R + V_L + V_C = RI_0\sin{\omega t} + (\omega L – \frac{1}{\omega C})I_0\cos{\omega t}\)
目標は\(V = RI\)の形にしたいんですよね。これをうまく式変形するには、三角関数の合成ですね。数学をやっているあなたならできて当然です。
\(a\sin{x} + b\cos{x} = \sqrt{a^2 + b^2} \sin{(x + \alpha)}\)(ただし、\(\tan{\alpha} = \frac{b}{a}\))
これを利用すれば
\(V = \sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2}I_0\sin{(\omega t + \alpha)}\)
(ただし\(\tan{\alpha} = \frac{\omega L – \frac{1}{\omega C}}{R}\))
と表すことができます。これで\(V = RI\)の形になりましたね。
位相差とインピーダンス

次に交流ではおなじみの「交流→直流」の変換をしていきます。そうです。実効値を使うんでした。
実効値は最大値から来ているので、先ほどの式から最大値を考えるとこうです。
\(V_0 = \sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2} I_0\)
\(実効値 = \frac{最大値}{\sqrt{2}}\)
なので、両辺に\(\frac{1}{\sqrt{2}}\)をかければ
\(V_e = \sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2}I_e\)
まさにオームの法則ですね。
 AI
AI
まさに\(V = RI\)ですね。
直流回路に見立てたとき(見立てなくてもですが)の抵抗が
\(Z = \sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2}\)
となるわけです。これがいわゆる合成抵抗というもので、正式な名前はインピーダンスです。
インピーダンスって合成抵抗のことだったんですね!
 AI
AI
また、位相差について考えると見ての通り\(\alpha\)だけずれてますね。
これでRLC直流回路について完璧に理解できましたね。
直流共振回路

最後にこの回路に関して補足をしたいと思います。
先ほど見たように直流回路において抵抗の役割を果たすものなので、この値が小さいほど電流が流れやすくなるわけですね。
日常生活の電気は交流ですから、できる限りインピーダンスを小さくして、より小さい電圧でより大きい電流を各電化製品に流したいわけです。
そこで一番インピーダンスを小さくさせるにはどうしたら良いか考えてみます。
\(Z\)の式を見ると角周波数の\(\omega\)が含まれていますね。これは周波数\(f\)の親戚みたいなものです。
つまり、交流電源によってこの\(Z\)の値が変わるわけですね。
\(Z\)を一番小さくするためにはルートの中身の
\(\omega L – \frac{1}{\omega C}\)
を0にするべきですね。
つまり
\(\omega = \frac{1}{\sqrt{LC}}\)
振動数に置き換えれば
\(f = \frac{\omega}{2\pi} = \frac{1}{2\pi \sqrt{LC}}\)
この\(f\)は交流電源で操作できるので、意図的にインピーダンスを最も小さくでき電流を最大限に流すことができるのです。
この\(f\)を固有振動数と言います。
問題で問われることもありますが、問題を解くだけだとどうしてもこの意味を理解できないんですね。
このように実生活と関連付けると、「電化製品を楽に使うために固有振動数が使われているのか」と理解が深まるのです。
並列回路についてはこちらで解説しているので合わせてチェックしましょう。
絶対に覚えるな!

いかがでしたか?
実はやっていることは直流と何も変わらないわけです。難しく見えるのはsinやcosの式が出てきたり、交流ならではの位相のずれなどを考えるってことだけで
基本は電圧マークを書いて「一周した電位=0」を使っているだけですね。
僕はインピーダンスとかリアクタンスを覚えてほしくはありません。できる限り導出して、それをこなしているうちに自然と覚えた。そういう感覚を身に付けてほしいです。
直流のときの合成抵抗や合成容量のときにも僕は覚えろなんて一言も言っていません(というより合成する必要がありません)
なので絶対に覚えないでください!
それでは。









Comment
コイルの位相が〜のところ間違えますよ
あと、その下のωがomegaになってます。
指摘ありがとうございます!