反射板のドップラー効果問題を解説!「風」や「うなり」も問われます!

Akinoriさん。ドップラー効果やってたら反射板の問題が出てきたんですよ。どう対処すべきかわからないです。
 AI
AI
わかった。反射板ってどんな役割があると思う?
 AKINORI
AKINORI
それはもちろん、波を反射するんですよ。
 AI
AI
そうだね。つまり、受け取った波を発する。要は観測者と音源の役割を同時に担ってるんだ。これがポイントだよ!
 AKINORI
AKINORI
ドップラー効果ではよく反射板のある問題が出てくることが多い。
初見では反射板がをどう扱っていいのかわかりませんよね。
でも素直に考えてみれば大丈夫です。
反射板は受け取った波を反射して送り出す
つまり、観測者であり音源である
こう考えればもう解けたようなもんです。
では一題見てみましょう。
ドップラー効果についてはこちら
問題
図のように観測者O、振動数\(f\)の音源S, 反射板Rが一直線上にならんいる。音速を\(V\)とする。O,Sは静止しており、Rは速さ\(v\)で左向きに動いている。
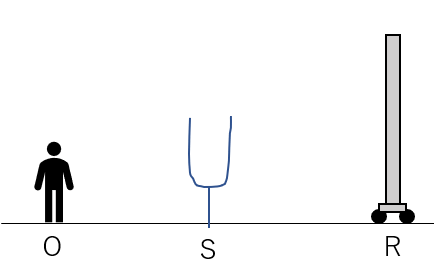
(1)観測者が聞く反射音の振動数を求めよ
(2)風が左向きに一定の速さ\(w\)で吹いているとき、観測者が聞く音の振動数を求めよ
(3)(2)において、1秒当たりの観測者が聞く音のうなりの回数を求めよ
(1)反射板は「観測者&音源」
「観測者&音源」とはどういう意味かというと・・・
はじめ、反射板は音を受け取る。
つまり観測者として考えればいいんですね。
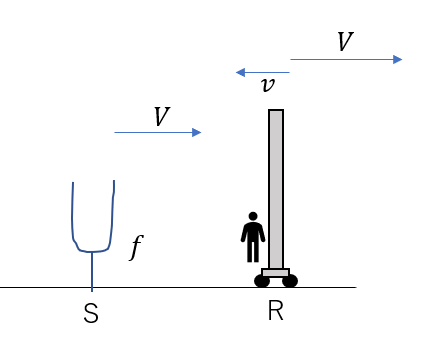
反射板が受け取る振動数\(f_R\)は
矢印の長さを並べればよかったんですよね。
上から観音様の順に。
\(f_R = \frac{V + v}{V}f\)
これが反射板Rが受け取る振動数です。
そして、反射板はこの振動数の波を発信する。
つまり次は、音源として考えれば良いですね!
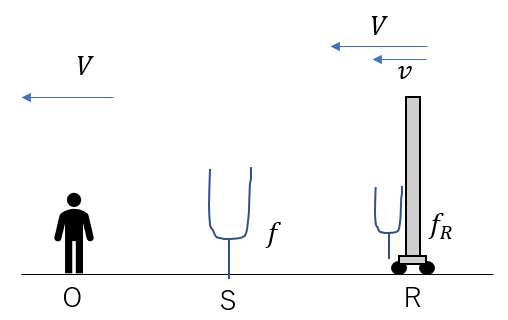
同じように観音様で並べれば、観測者が聞く音の振動数\(f_O\)は
\(f_O = \frac{V}{V – v}f_R = \frac{V + v}{V – v}f_R\)
これが答えです。
なるほど!まず観測者として見て、次に音源として見るんですね!
 AI
AI
(2)風は音速に影響する
(2)は風が吹くという条件がありますね。
音は空気中を進む波ですから、風によって速さが変化します。
それに注意して同じように考えればいいだけですね。
まず、反射板を観測者に見立てて考えましょう。
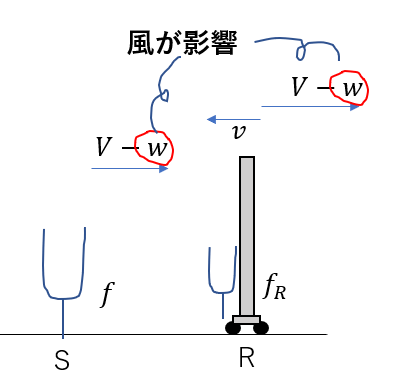
音は右向きに進んで行きますが、風は左向きに吹いています。
つまり、音はその分遅くなります。なので矢印の長さは\(V – w\)となります。
あとは、さっきと同じように公式に当てはめましょう。
上から観音様です。
\(f_R = \frac{V – w + v}{V – w}f\)
次は反射板を音源に見立てて考えます。
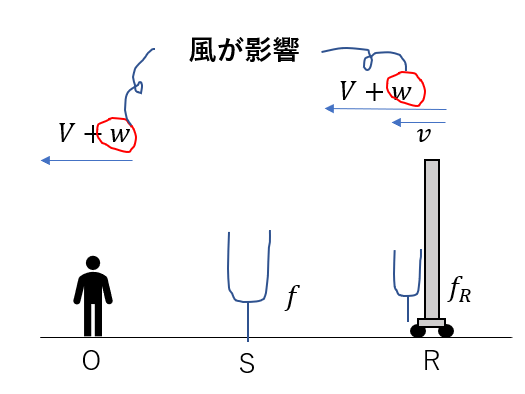
やっぱりここでも風が影響してきます。
今度は音が左向きに進み、風も左向きに吹くので、今度は音速は増します。
なので、矢印の長さはプラスされますね。
あとは同じ。観音様で並べればOKです。
\(f_O = \frac{V + w}{V + w – v}f_R = \frac{V – w + v}{V + w – v} \cdot \frac{V + w}{V – w}f\)
これが答えですね。
風が吹いたら音速が変わる!これがポイントですね。
 AI
AI
(3)うなりは振動数の差
ラストはうなりの問題です。
うなりは振動数の差によって求められます。
今回は、音源Sから直接聞く音と、反射板Rによって聞く音によってうなりが生じます。その1秒間の回数を調べます。
反射板による振動数は(2)で求まっていますね。
そして、直接聞く音についてですが、
音源Sも観測者Oも止まっています。
だからドップラー効果とかないです。
音源Sの振動数\(f\)がそのまま観測者の聞く振動数になります。
\(f_O = f\)
そして、1秒間に聞くうなりはこの振動数の差です。
1秒あたりのうなりの回数\(f\)
\(f = |f_1 – f_2|\)
ということで、うなりの回数\(f’\)は
\(f’ = f_R – f_o = \frac{2vV}{(V + w – v)(V – w)}f\)
これが答えになります。
うなりは絶対にプラスにしないといけないので、もしマイナスになったら絶対値をつけてプラスに直してください。
なるほど!すごい分かりやすかったです。ドップラー効果って簡単ですね!
 AI
AI
そう!反射板があるときは「観測者→音源」という流れで見立てるといいんですね。
 AKINORI
AKINORI
まとめ
- 反射板があるときのドップラー効果
反射板を「観測者」に見立て、次に「音源」に見立てる
- 風が吹くとき
音速に影響する
それでは!









Comment
とても分かりやすかったです!反射板はまず観測者として音源から音を受け取り、その音を今度は音源として観測者に伝えるんですね!
三角形の2つの頂点から動きながら異なる周波数の音が発された場合、うなりはどうやって計算したらいいですか?
同じように、ドップラー効果を考えれば大丈夫です。
もし音源が観測者に向かって動いていない場合は、音源の運動を分解して、観測者に向かう(あるいは遠ざかる)向きだけを考えます。