それ間違ってます!運動方程式の意味と正しい立て方とは?

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
運動方程式の立て方が分からないんですが、何かコツはありますか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
物理において一番重要な公式が運動方程式です。
運動方程式から様々さ公式を導けます。運動方程式はすべての根源となる式です。
ですが、運動方程式を多くの高校生が間違って覚えていたり、間違った立て方をしています。
\(ma=F\)の\(F\)は「力」ではありません!
そもそも運動方程式は\(ma=F\)ではありません!
この記事では、高校生が間違っている覚えている運動方程式を正しく解説します。
最後まで読むことで、運動方程式の意味が分かり、正しく立てる方法もわかります。
運動方程式の意味が分かる
運動方程式の立て方がわかる
目次
運動方程式とは?

運動方程式は、1つの物体について成り立つ関係式のことです。
加速度、質量、合力についてこのような関係式が成り立ちます。
・・・美しいですね。
運動方程式の勘違いポイント4つ

もちろん知っているかと思いますが、多くの高校生がこの式に関して勘違いしていることが4つあります!
この間違いを正しさないと、後々ヤバくなるのでここで正しい理解をしてください。
運動方程式はベクトルの関係式
「運動方程式って何?」と聞くと
「(質量)×(加速度)=(力)」や「ma = F」
と答えますよね?
ですがどちらも間違いです。
\(ma = F\)ではなくて
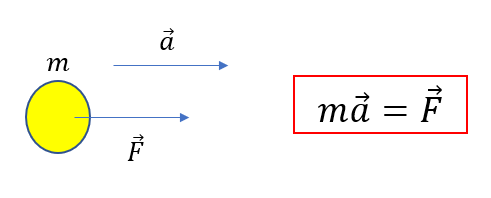
\(m\vec{a} = \vec{F}\)なんです。
運動方程式は、ベクトルの関係式なんです!
ベクトルを扱うということは、
自分で軸を設定して考える必要があるということです。
ベクトルについては以下の記事で詳しく説明しているのでチェックしてください。
運動方程式の\(\vec{F}\)は「合力」
運動方程式には\(\vec{F}\)が含まれています。
いわゆる「力」ですが、単純に力と考えると危険です。
この\(\vec{F}\)は合力です。
合力というのは物体にはたらく力をすべて足し合わせたものです。

運動方程式ではこの合力を使わなければいけないのです。
加速度と合力は同じ方向

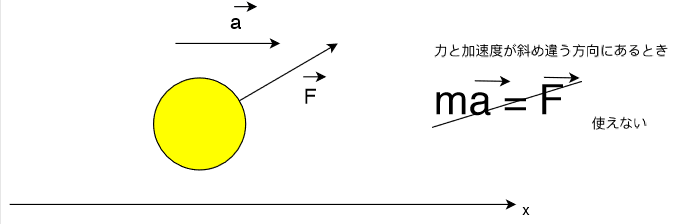
運動方程式\(m\vec{a} = \vec{F}\)をよく見てみましょう。
\(m\)はスカラー(向きがなく大きさのみ)です。もっと言えば「定数」です。
ベクトルが定数倍で表現できるときは2つのベクトル平行です。
合力が加速度の定数倍になっていますから
合力と加速度は同じ方向にある
ということが分かりますね。
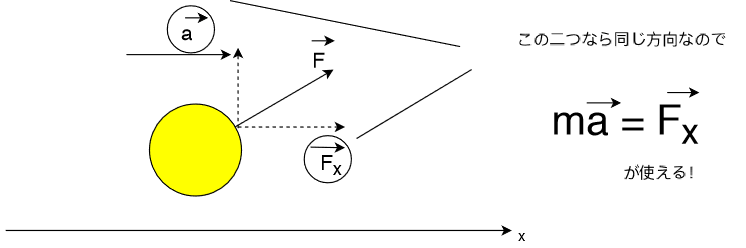
加速度と合力が同じ方向にあるってことは、加速度と合力が一直線になるようにして考えろということです。
向きが異なる場合は、ベクトルを分解して、平行になったもの同士で考えればいいのです。
運動方程式は原則1物体で考える
これ、かなり大事です。
例えば2つの物体があるとします。
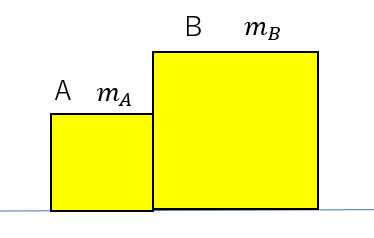
これについて運動方程式を立てるときに、こんなミスをやる人が多いです。
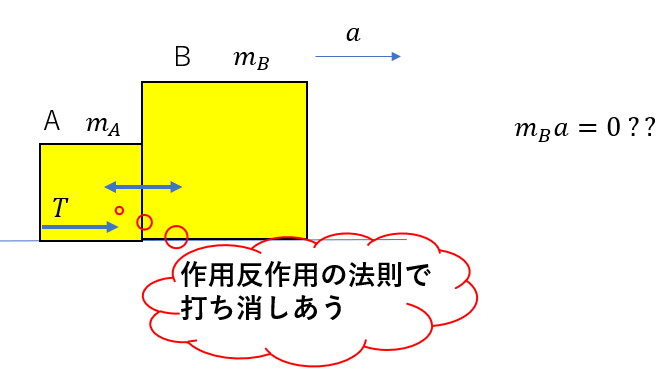
Bについてこのように運動方程式を立ててしまう人がいます。これは間違いです。
2物体があると(特に密接していると)両方を一気に見てしまいがちです。
ですが、この作用反作用にある力は働いている物体が違います。
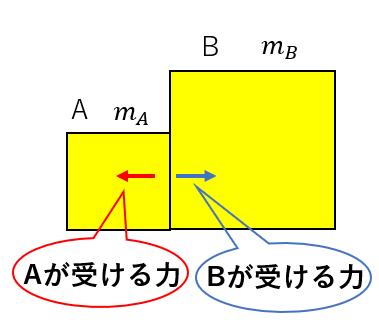
このように、見ている対象が違います。
Bについて運動方程式を立てるなら、Bが受ける力のみを使わなきゃいけません。
これは慣れてきてテキトーにやるほどミスしやすいので注意しましょう!
運動方程式の役割

運動方程式は質量、加速度、合力という情報がありますが、運動方程式は99%加速度を求めるために使います。
質量は測れるものですし、力も重力、摩擦力、張力・・・とどれも測れます。
ですが、加速度は物体の運動が複雑になればなるほど求めにくくなります。
また、加速度を求めるということは物体の運動の仕方を求めるということです。
ある時間\(t\)の加速度が分かれば\(t\)での速度もわかります。速度が分かれば\(t\)での位置もわかります。
その運動の仕方を質量と力という既に分かっているものから予測することができるのです。
そういう背景もあって、運動方程式は加速度を求めるために使います。
運動方程式の立て方

運動方程式の役割、そして4つのポイントが理解できたことで、運動方程式の立て方も分かります。
- 注目する物体を決める
- 軸を取る(原則、加速度の向き)
- 力を書く
- 合力を求める
- 運動方程式を適用
この手順を正確に行っていけば絶対に間違えることはありません。
この手順を踏めば、
- 作用・反作用の関係にある力をまとめてしまう
- 合力を求め忘れる
- 符号を間違える
というミスをしなくなります。
慣れないうちはもちろん、慣れてきてもこの立て方を守りましょう。
運動方程式を実際に立ててみよう
では、この運動方程式の立て方にしたがって、実際に運動方程式を立ててみましょう!!
質量がともに\(m\)の物体A,Bが軽い糸でつなげられている。AとBが滑らかな床に置かれている。物体Bに大きさ\(F\)の力を水平面から\(\theta\)だけ上向きに加えた。このとき各物体の加速度を求めよ。
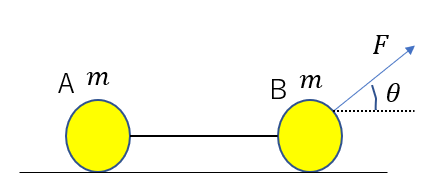
※問題文に出てくる文字は、「力」でも「力の大きさ」でも同じ\(F\)を使うことが多いです。当サイトではこの二つは使い分けていますが、問題集ではベクトルなのかスカラーなのか必ずチェックしておきましょう。
この問題を先ほどの運動方程式の立て方に沿って解いていきましょう。
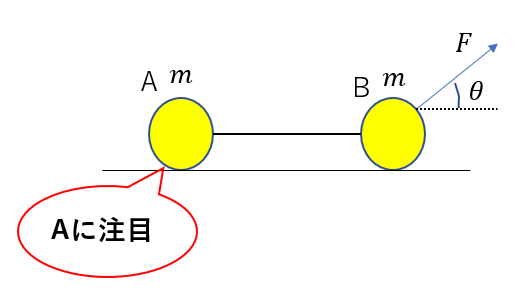
Step 1:注目する物体を決める
まずは注目するぶったいを1つ決めます。
まずはAについて考えます。
これ以降はBの情報は一切関係ありません。Bが受ける力などは完全に無視です。
Step2:軸を取る
軸の取り方ですが、なるべく加速度が生じる向きに軸を取ります。
加速度を求めるので、加速度に正の向きを合わせた方が混乱しないので加速度の向きに軸を取りましょう。
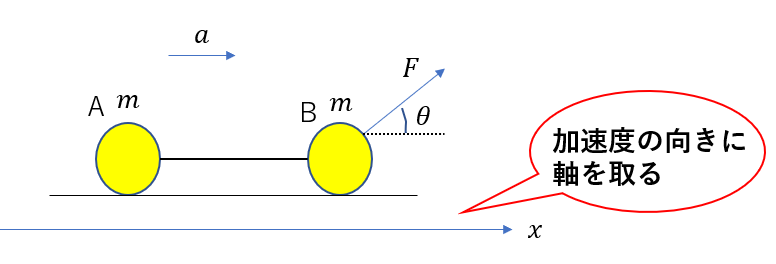
今回は加速度が右向きに働くと予想できるので右向きに軸を取ります。左向きに取っても大丈夫です。
軸の取り方では答えは変わらないので安心してください。
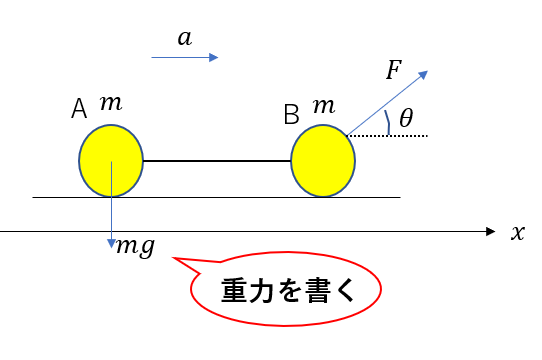
Step3:力を書く
ここステップが超重要です。
力を1つでも書き忘れると詰みますので、ここは慎重に行きましょう。
力を正確に書きだす方法を教えます。
- 遠隔力(重力)を書く
- 物体を一周して接するところで力を書く
まずAの重力を書きます。
次にAの周りを1周して別の物体が接触した部分で力を書いていきます。
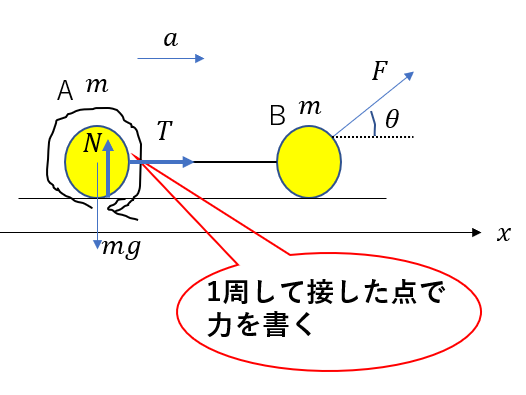
力を書いていくと図がごちゃごちゃします。なので図はできる限り多く書くことをオススメします。
また、すべての力を書くことがベストですが、今回のように明らかに水平方向にしか動かないと分かれば、水平方向のみの力を書くというのもOKです。
Step4:合力を求める
運動方程式では合力を使うので、これを求めます。
力を足していくのですが、力には向きがあるのでプラスマイナスを考慮しないといけません。
水平方向の力は糸の張力のみがはたらいています。
向きは軸と同じ向きなので\(+T\)ですね。
なので合力の大きさは\(F = T\)となります。
Step5:運動方程式に成分を代入
あとは、運動方程式に代入するだけです。
\(m\vec{a} = \vec{F}\)
\(ma = T\)
Aについて運動方程式を立てました。
Bについても同様に立てる
同様にBについても立てていきます。やることは同じなので流れは省略しますが、2つだけ注意点を伝えますね。
まず、外力が斜め上向きにはたらいています。しかし、加速度は水平右向きに生じると考えているので、一直線になっていません。
なので、外力は水平・鉛直に分ける必要があります。
また、AとBは糸でつながっており同じ運動を起こします。つまり加速度はAとBで同じです。
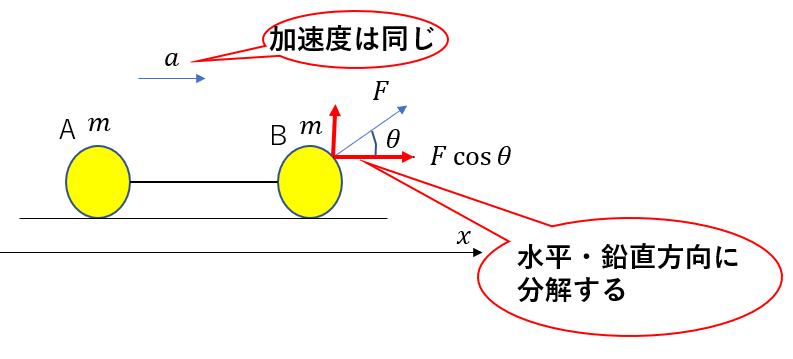
水平向きの力は張力と外力の二つがあります。
張力は、大きさが\(T\)で向きが逆なので\(-T\)です。
外力は、同じ向きなので\(+F\cos{\theta}\)です。
これを足して合力を求めて、運動方程式を立てると以下のようになります。
\(ma = F\cos{\theta} – T\)
ここまで求めた二つの式から加速度が求まります。

問題文は「加速度を求めよ」なので、向きと大きさを答えます。
つまり「右向きに\(\frac{F\cos{\theta}}{2m}\)」が答えです。
軸を左向きに書いたら?

STEP2で軸を左向きに取ると答えがマイナスで出てきます。
つまり\(a = -\frac{F\cos{\theta}}{2m}\)です。
このマイナスは逆向きを表します。
「最初は左向きに設定していたけど、実は右向きだったんだ」
ということが分かるのです。なので軸の取り方で答えは変わりません。
まとめ:運動方程式の立て方はマスターしよう

いかがでしたか?
運動方程式は一番重要な公式です。運動方程式の立て方を間違えてしまうと大変です。
複雑になればなるほど、この立て方に沿って解いた方がはやいですし、ミスも減ります。
しっかりマスターしてくださいね!
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!