【楽勝】浮力の公式とは?浮力の問題の注意点は3つだけ!

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
今日は浮力について扱っていきます。
浮力の公式は皆さんご存知かと思います。\(F = \rho V g\)です。しかし、\(F = \rho V g\)のそれぞれの文字が何を表しているかご存知ですか?
\(\rho\)は密度、\(V\)は体積・・・ではありません!!
そして、浮力の問題はたった3パターンしかないということを知っていましたか?
この記事では、浮力の公式の導出とその結果の本当の意味を教えていきます。そして、浮力の問題の3パターンもチェックしていきます!
最後まで読んで、入試の応用問題も解けるようになりましょう!!
浮力の公式の導出方法が分かる
浮力の公式の本当の意味が分かる
浮力の問題の3パターンが分かる
目次
浮力とは?

ある液体の中に物体を入れると物体には浮力がかかります。
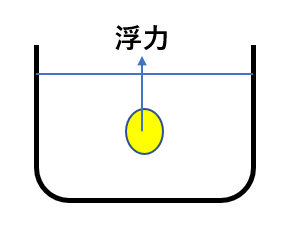
これは液体も分子でできているので、その分子が物体に衝突することで起こります。
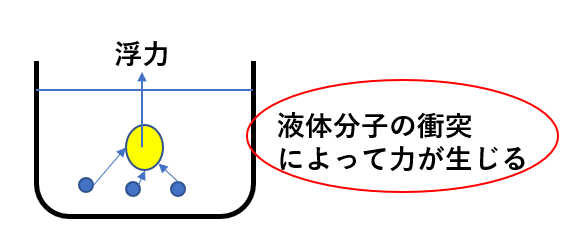
これは非常に重要なことなので頭に入れておいてください。
本当は無数の分子が衝突するので浮力は上向きと特定できないかもしれませんが、これは圧力という観点で見ることで証明することができます。
水圧の公式

先ほど液体分子が衝突することによって力が生じるという話をしました。
しかし、液体分子は無数にあり敷き詰められていると考えることができます。
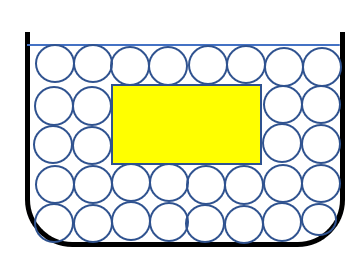
これを元に水圧を考えていきましょう。
水圧の導出

密度\(\rho\)、単面積\(S\)、高さ\(h\)の水の底面にかかる水圧を求めます。
圧力は単位面積当たりの力であり
\(p = \frac{F}{S}\)
と表すことができます。ですから、底面にはたらく力の大きさ\(F\)が求まればOKですね。
まず分子は互いに押し付け合っていますので、特に横方向には同じ大きさで向きが逆の力がはたらきます。
なので、図のように各分子の横方向の力は打ち消しあいます。
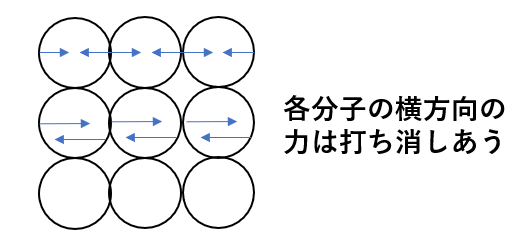
次に底面にかかる力を考えます。
分子1つ1つには重力がはたらくので、下の分子に力がどんどん伝わってきます。
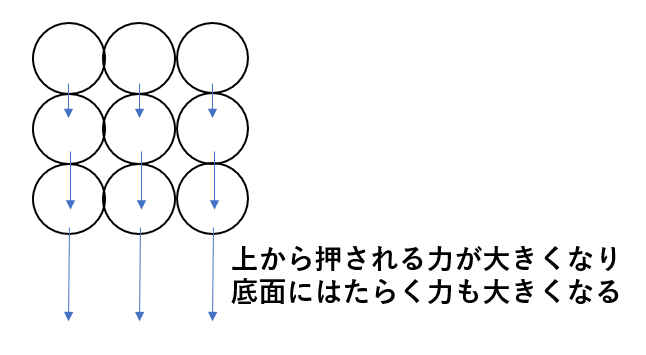
1番上の水分子の重力だけ2番目の分子は受けます。
その力と2番目の分子の重力の合計分、3番目の分子は力を受けます。
その力と3番目の分子の重力の合計が、底面にかかるというわけです。
つまり、分子の全重力が底面に働く力\(F\)となります。
質量は「密度×体積」と求められますので、
\(m = \rho \times Sh\)です。
つまり\(F = mg = \rho Sh g\)となります。
よって圧力はどうなるかというと
\(p = \frac{\rho Shg}{S} = \rho hg\)
このように表せます。
水圧
\(p = \rho hg\)
(*\(\rho\):水分子の密度、\(h\):水面から深さ)
水圧の意味
この式から、水圧は深さ\(h\)だけに関係し、深くなるほど水圧は大きくなるということです。
また、これは水分子で考えましたが、油でも海水でも、さらには空気でも同じことが言えます。
それぞれの密度を使って同じ式を立てることができます。
また、圧力は実際には四方八方にかかるものです。当然横方向にもかかります。
その大きさも深くなるほど大きくなります。
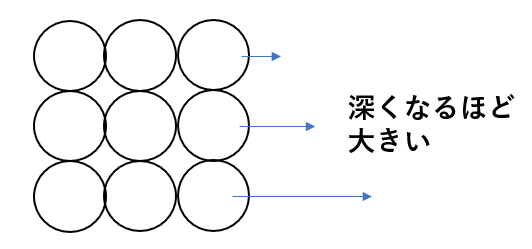
なのでペットボトルに穴をあけるとき、下の方が勢いよく水が出るのです。
浮力の公式を水圧から求めてみる
これを踏まえて浮力を求めてみましょう。
横方向の力は相殺される
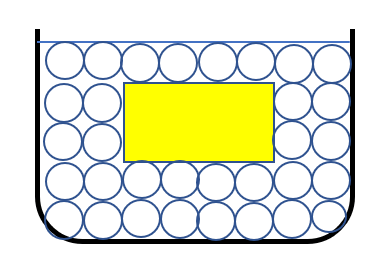
先ほどの通り、水分子の押し合いによって水中の物体にも力が働きます。
これを使って浮力を求めることができます。
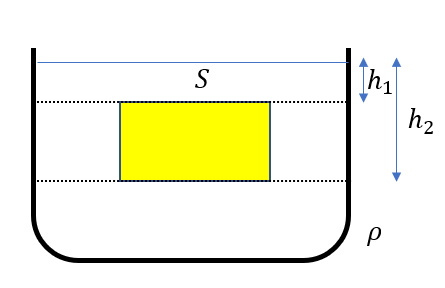
断面積\(S\)で上面と下面の深さがそれぞれ\(h_1, h_2\)の物体を密度\(\rho\)の水中に沈めます。
この物体には圧力によって力が働きますが、横方向の力は相殺されます。
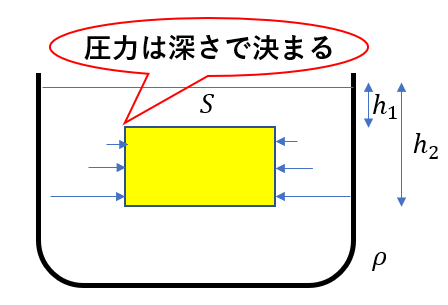
水圧は深さで決まるからです。深い部分の圧力は大きくなりますが、左右それぞれで同じ大きさだけ受けるので打ち消しあいます。
なので、上面と下面の圧力を考えればいいですね。
上面と下面の力の合力=浮力
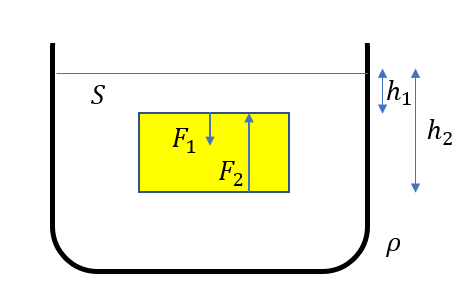
上面と下面の圧力はそれぞれ
\(p_1 = \rho h_1 g, p_2 = \rho h_2 g\)
です。
なので上面と下面が受ける力の大きさは以下のようになります。
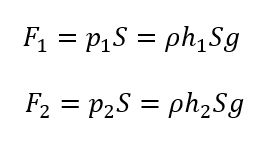
向きは上面が下向き、下面が上向きです。なのでこれらの合力の大きさ\(F\)はこのように表せます。
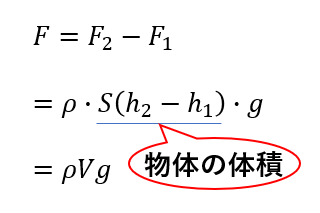
これが浮力の大きさになります。向きは上向きです。
式変形していくと\(S(h_2 – h_1)\)というのが出てきます。
これは物体に関して「底面積×高さ」となっているので物体の体積に置き換えることができます。
もちろん水だけでなく、どんな液体、さらには気体でも成立します。
この液体や気体のことをまとめて流体と呼びます。
浮力の大きさ
\(F = \rho V g\)
\(\rho\):流体の密度、\(V\):流体中の物体の体積
浮力の公式の注意点

浮力の公式は覚えている人も多いかと思います。しかし、大事なのは各文字が何を表しているかです。
\(\rho\)は流体の密度であり、物体の密度ではありません。
\(V\)は流体中物体の体積であり、流体の体積ではありません。
ここを混同するミスが多いので注意して欲しいです。
これは浮力に限った話ではありません。各文字が何を表しているかは非常に重要です。
そこまで覚えて「公式」です。
浮力の公式とアルキメデスの原理

この浮力についてもう一つ特徴があります。
\(F = \rho V g\)の\(\rho V\)に注目しましょう。
\(V\)は物体の体積ですが、同時にそこにあった流体の体積でもあります。
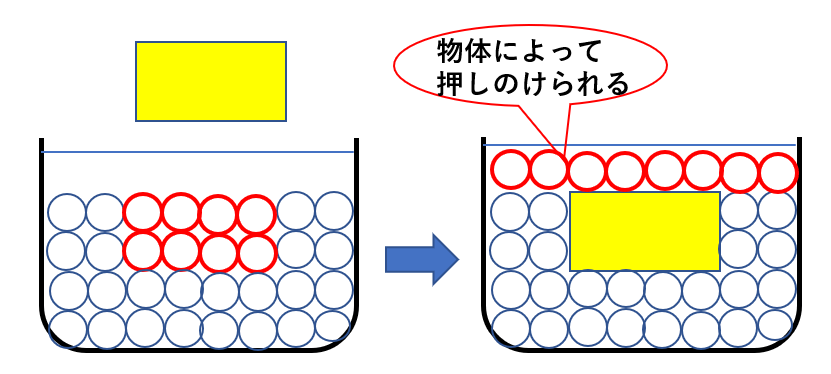
図のように、粒8個分の大きさの物体を沈めたら、8個分の粒が外に押し出されます。
物体を流体の中に入れることで、そこにあった流体は押しのけられるのです。(消えるわけではありません)。
お風呂に入ると水面が上昇しますよね。あれは自分の体の分だけ水が押しのけられたからです。
つまり\(V\)は物体に押し出された流体の体積でもあります。
そして\(\rho V\)という形は「密度×体積」となっていますから、流体の質量です。
それを踏まえてもう一度浮力の式を見てみます。

「質量×重力加速度」なので重力ですよね。
つまり、物体によって押しのけられた流体の重力の大きさだけ浮力が生じるということです。
これをアルキメデスの原理と呼ばれています。
これはよく考えたら当たり前です。

赤色の粒をひとまとまりで考えると、その重力の大きさだけ垂直抗力を受けます(静止していると考える)。
その赤い粒を物体に置き換えただけの話ですから、赤い粒の重力の大きさだけ浮力を受けるのです。
浮力の問題は3つだけ

浮力については理解ができましたね。
では、浮力を使った問題はどのような問題が出るのでしょうか?
実は浮力を使った問題は3パターンしかありません。
物体の一部が外に出ている問題
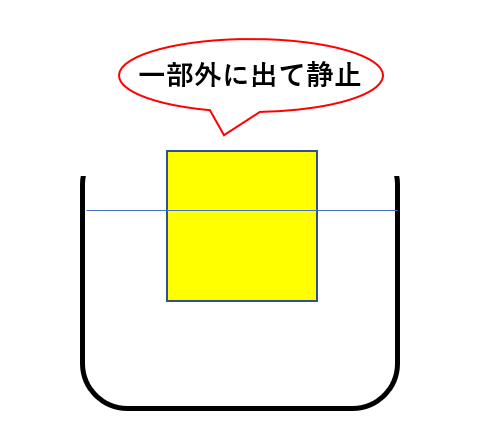
センター試験レベルとして物体が一部外に出ているときの力のつり合いを考える問題があります。
大事なのは浮力の公式の\(V\)は流体内にある物体の体積というところです。
そこに注意すればOKです。
また、これに関連して異なる流体に挟まれた場合を考えることもあります。

この場合もどちらの流体にどれだけ体積が含まれるかを考える必要があります。
また、密度も違うので、それぞれの密度を適用する必要があるところにも注意しましょう。
浮力による単振動の問題

入試標準レベルとして浮力による単振動の問題が問われます。
単振動はばねだけではありません。その代表例として浮力を扱います。
単振動の知識と浮力の知識を合わせて考える必要があるんで1度解いてみるといいでしょう。
浮力による単振動の問題はこちらで詳しく説明してます。
液面が変化する問題
入試難関レベルとして、液面が変化する問題を考えることもあります。
東工大の2017年の問題でこの問題が出ています。
例えば、物体を液面から出していくと水面が低くなります。
つまり、物体を上にあげた分と水面が下がった分の両方を考慮して体積\(V\)を決定する必要があります。
一度東工大の過去問を見て解いて見るといいでしょう。
まとめ:浮力の公式と3つの問題パターン

いかがでしたか?
\(F =\rho Vg\)と数式のように覚えていると、各文字が何を表しているか分からなくなります。
導出→公式の意味を理解→使い方の理解
この流れを忘れずに勉強をしていきましょう!
水圧の式:\(p = \rho hg\)
浮力の式:\(F = \rho Vg\)
\(\rho\):流体の密度、\(V\):流体中の物体の体積
入試で出る問題3パターン
- 物体の一部が外部に出ている問題
- 浮力による単振動の問題
- 液面が変化する問題









