物理の重心とは?【重心の求め方に公式はありません!】

どうも!オンライン物理塾長あっきーです!現役で早稲田大学に合格し、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
重心の意味やその求め方がよくわかりません。応用問題になると公式通りに当てはめられないです…
 リケジョ志望のAIさん
リケジョ志望のAIさん
今回はこのような悩みを解決します。
多くの高校生が重心の公式を暗記しようとします。
結論から言うと、重心の求め方に公式はありません!!
大事なのは重心の意味を理解してそこから求め方を導き出すことです。
この記事を読むことで、重心の公式を覚える必要がなくなるだけでなく、応用問題(切り抜き図形の重心)も解けるようになるので最後まで読んでください!!
目次
物理の重心とは?
日常生活でも物理でもよく「重心」という言葉が出てきまが、ほとんどの高校生がその意味を正確に答えられません。
「重力の中心」では50点です。
100点の解答は「質量の代表点」です。
物理の重心は重力の中心となる
まず「重力の中心」の説明をします。
図のように、ある剛体を細かく分割していきます。
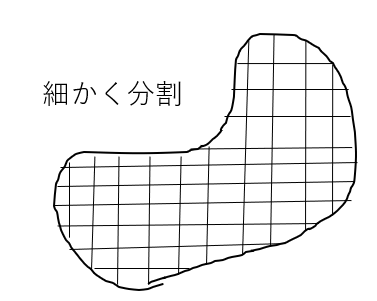
すると、分割したもの1つひとつに重力が働きます。
それをどんどん足し合わせていくと一つの重力(の合力)になりますね。
元の剛体を分解して、それを足し合わせただけですので、この重力(の合力)は分割する前の剛体に働く重力です。
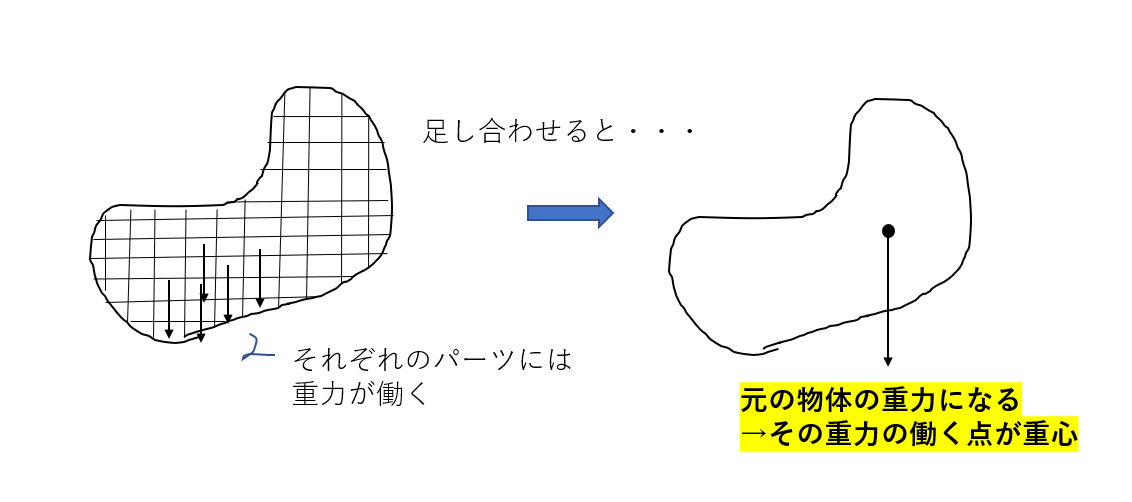
このときに重力が働く点を「重心」と呼びます。
各物体を合わせたときの重力のなので「重力の中心」ということなんです。
物理の重心の本来の意味
これがよくある説明ですが、重心の本当の意味は別にあります。
先ほどの通りに考えれば、次のような質量\(m_1, m_2\)の物体の重心については図のように考えられます。
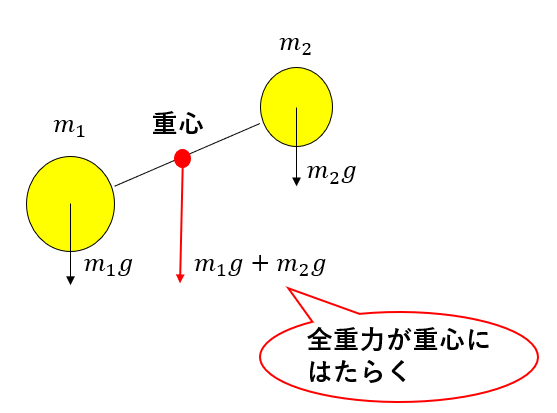
この考え方からもう一歩進むことで、難関大の入試問題が解けるかどうかが決まります。
重心の本来の意味とは何でしょう?
それは・・・
「質量の代表点」
です。
物理の重心は「質量の代表点」
先ほどの重心に働く重力は
\((m_1 + m_2)g\)
と表せます。
\(m_1 + m_2\)は質量の和、つまり全質量です。それに\(g\)を掛けた形になっています。
これは
「重心に全質量が集まっていると考えることができる」
ということを表しているのです。
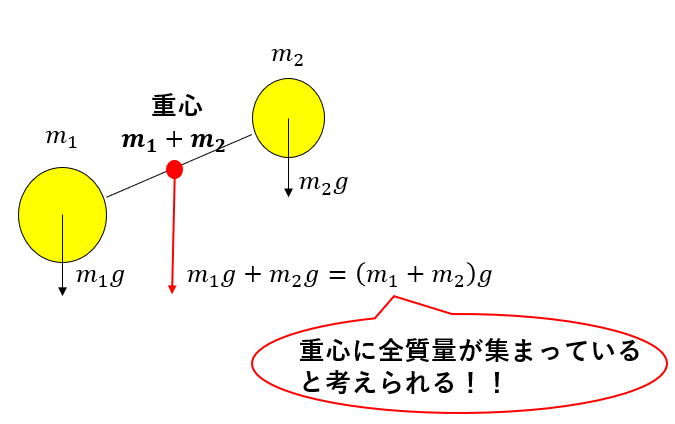
重心に質量\(m_1, m_2\)が集まってそれが重力を受けると考える。これが重心の真の意味です。
重心とは「質量の代表点」ということなんです。
物理の重心は「運動の代表点」となる
と、これだけ話しても「重力だろうと質量だろうと変わらないじゃねーか!」と突っ込まれそうですが、この違いこそが合否を分けます。
それは「二体問題」に現れてきます。
入試では図のように、ばねでつながれた二物体の運動について問われることが多いです。
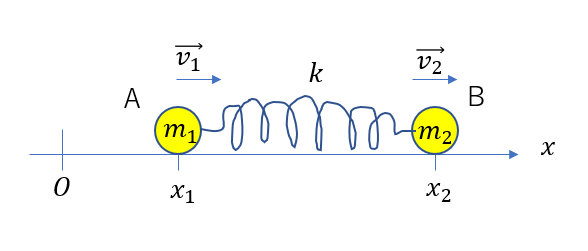
ですが、この運動ってイメージしにくいですよね。
「二つの物体がばねによって振動しながら、全体として右に動く」まるでイモムシみたいな運動をするわけです。
難しいですよね。実際に入試でも出ます。
しかし、この運動を「重心」で考えると、とてもすっきりするんですよ。
さっきみたように重心は「全質量をもった点」です。
また、運動方程式を見てみると
\(m\vec{a} = \vec{F}\)
ですよね。運動方程式は物体の運動の様子を見極める大事な関係式でした。
とくに、\(m\)は「質量」でしたね。
重心に関して、運動方程式を適用すると
全体の運動の様子を見極めることができるのです!!
先ほど確認したように、重心は「質量の代表点」ですから
あたかも全質量が重心にあるかのようにみなせるので、重心の運動は全体の運動を代表できるのです。
つまり、重心は「運動の代表点」と言えるんです!
「重力の中心」と考えると、運動の代表点というのはつかみづらいですが、
「質量の代表点」と考えると、運動方程式を考えることができ、結果的に運動の代表点とすることができるのです。
この「2体問題」に関してはこちらの記事をチェックしてください!
物理の重心の位置の求め方と公式
重心の意味について確認できたので重心の位置の求め方を見ていきましょう。
ここまでの重心の性質を理解できれば、重心の位置の求め方が自然と分かります。
質量\(m_1, m_2\)と軽い糸でつながっている剛体がある。この剛体の重心の位置のx成分、y成分を求めよ。重力加速度の大きさは\(g\)とする。
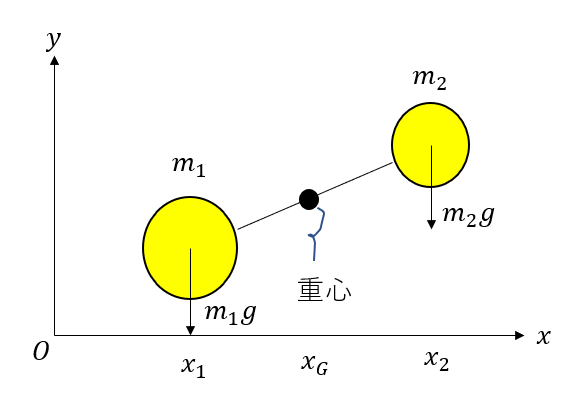
先ほど見たように、重心は「質量の代表点」です。
とにかく代表なので、「重力のモーメントの代表点」とも考えられますね。
ということは、
(重心の重力のモーメント)=(各重力のモーメントの和)
という式が成り立ちます。
重心には
\((m_1 + m_2)g\)
の大きさの重力がかかることは先ほど確認しました。
そして、重心は「モーメントの代表点」と考えますので・・・
原点回りのモーメントを考えます。
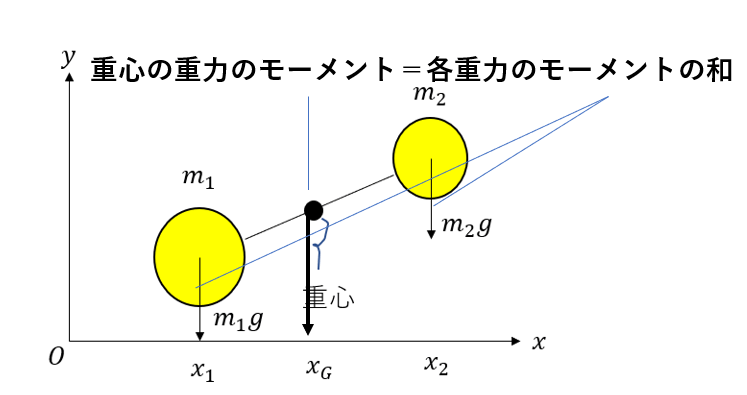
\((m_1 + m_2)g x_G = m_1g x_1 + m_2g x_2\)
\(x_G = \frac{m_1x_1 + m_2x_2}{m_1 + m_2}\)
これが重心の\(x\)座標となります。
じゃあ、y成分は?
というと、この図を90度回転させて考えればいいですね。
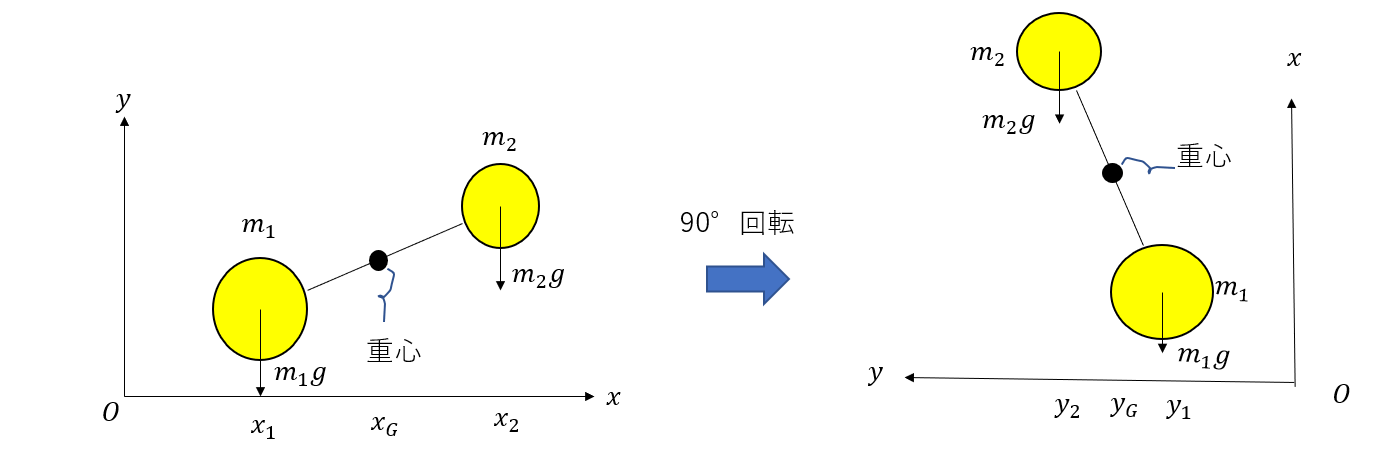
そうすれば、全く同じように求められます。
\(y_G = \frac{m_1y_1 + m_2y_2}{m_1 + m_2}\)
このようにして、重心の位置は求められます。
重心の位置に公式なんて無い!!
教科書とかでは、この重心の位置を公式として載せています。
\(x_G = \frac{m_1x_1 + m_2x_2 + ・・・}{m_1 + m_2 + ・・・}\)
\(y_G = \frac{m_1y_1 + m_2y_2 +・・・}{m_1 + m_2 +・・・}\)
ただ、こんなの全く覚える必要なんてありません。
今やったように「質量の代表点」ということが分かっていれば導けるわけですからね。
公式を使おうとすると、切り抜き図形の重心などの応用問題でおそらく混乱するので、重心の性質を考えたうえでモーメントを使ったうえで重心を求めてください。
その切り抜き図形の問題についてはこちらで分かりやすく説明しているのでぜひ見てください!
まとめ:重心の意味と求め方
いかがでしたか?
重心の意味と求め方は必ず理解してくださいね。
- 重心の本来の意味
「質量の代表点」
・重力の代表点
・運動の代表点
は「質量の代表点」からわかる部分的な解釈。
- 重心の運動を見ると複雑な運動も単純化できる
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!










