【熱力学】2022年自治医科大の物理問題解説
問題
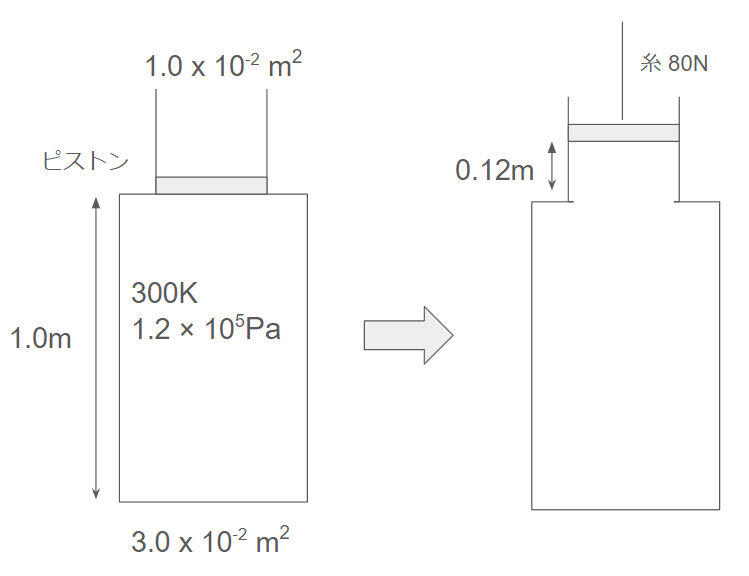
図のように、 底面積 3.0 × 10-2m²高さ1.0mの円筒容器の上部に、 断面積1.0×10-3m² の円筒管を付けたある質量の断熱容器がある。 この容器に温度300K で容器の外と同じ圧 力 1.2 × 105 Paの理想気体を入れ、 円筒管の最下部に断熱性の軽いピストンでふたをする。次に, ピストンの中心に糸を付け、その糸で容器全体をつるすと, ピストンは上に0.12m移動 した。 このときの糸の張力は80Nであった。 気体の温度は何K下がるか。 最も近いものを選べ。
㋐ 0 ㋑ 1 ㋒ 3 ㋓ 6 ㋔ 9
熱力学で重要なこと
まず熱力学の分野では使う公式は以下の2つです。
- 状態方程式 \(PV = nRT\)
- 熱力学第一法則 \(Q = \Delta U + W \)
そして熱力学の問題が出たときには以下のステップを必ず踏みましょう。
- 各状態を整理
- 状態変化の中で「一定」を探す
熱力学の問題は基本的にこれだけですべて解けてしまいます。
それでは早速解いていきましょう
各状態を整理する
まずは各状態を整理しましょう。
熱力学では、公式にある通り、圧力P、体積V、温度Tも情報が必要です。これを整理していきます。
状態1
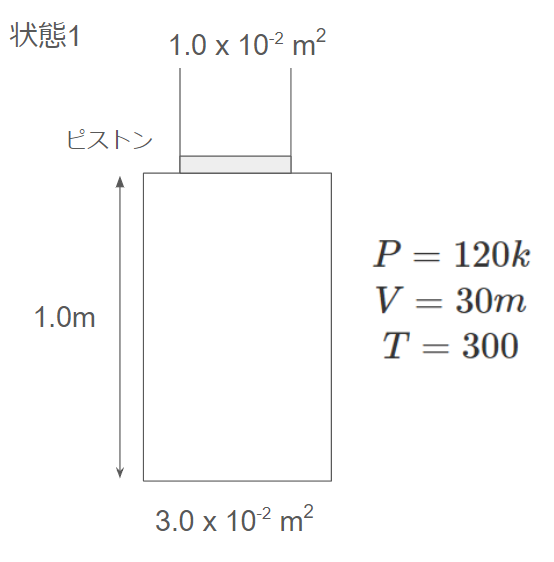
圧力Pは記載の通り、120kPaです。
体積Vは30mm2 × 1.0 m = 30mm3 です。
温度Tは300Kです。
ちなみに、ここであえてk(キロ)やm(ミリ)を用いています。物理ではよく10の何乗というような値をよく使いますが、計算の時に毎度書くと乱雑になりますし計算ミスが起こりやすいです。なのでk(キロ)やm(ミリ)で表すとわかりやすくなります。
kは103, mは10-3です。
これはかなり使えるテクニックですのでぜひ使ってください。
状態2
まず圧力を求めましょう。
これはピストンの力のつり合いで求められます。
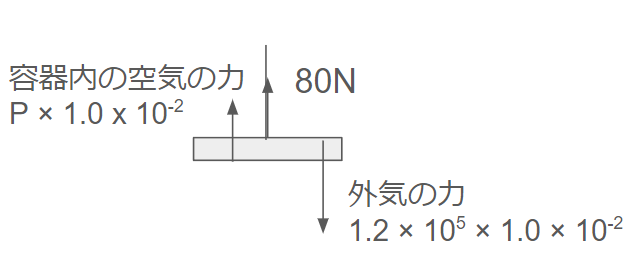
糸の張力が上向きに80N
容器内の空気の力は、圧力をPとして、\(P \times 1.0 \times 10^{-2}\)です。
圧力 × 底面積で力は求められます。
次に外気の力があります。これは問題文で「容器の外と同じ圧力 1.2 × 105 Paの理想気体を入れ」と書かれているので、外気の圧力は1.2 × 105 Paです。
なので外気の力は\(1.2 \times 10^5 \times 1.0 \times 10^{-2} \)となります。
後は力のつり合いの式を立てるだけですね。一部計算をしてしまいます。
\(80 + P \times 10^{-2} = 1.2 \times 10^3 \)
\(P = 112k Pa\)
これが内部の圧力です。
体積はピストンの上昇分も考える必要があるので
\(V = 3.0 \times 10^{-2} + 1.0 \times 10^{-2} \times 0.12 \)
\(V = 31.2 mm^3\)
となります。
状態2をまとめると以下の通りです。
圧力:\(P = 112k \)
体積:\(V = 31.2\)
温度:\(T\)
状態変化で一定を探す
後は気体の状態方程式を使いたいわけですが、\(PV = nRT\)の中で何が一定なのかを考えます。
今回は密閉容器なので気体の量、つまり\(n\) (モル)は変化せず一定ですね。
また\(R\)も気体定数なので変化しません。
つまり、\(\frac{PV}{T} = 一定 \)と言うことです。
後は状態1,2の値を入れていけばOKです。
\(\frac{120k \times 30m}{300} = \frac{112k \times 31.2m}{T} \)
\(T = 291.2 \)
求めたいのは温度の変化量なので
\(\Delta T = 291.2 – 300 = – 8.8 \approx -9.0 \)
つまり、約9K温度が下がるということなので答えは㋔となります。
熱力学は一番点数が安定する
熱力学は非常に点数が安定する分野です。
2つの公式と、状態変化を追うステップがしっかりできていればどんな問題でも解けます。
ぜひこのノウハウを他の問題でも利用して下さい。