波の干渉条件を分かりやすく解説！逆位相でも光路差でもなんでも来い！

• 波の干渉条件が覚えられない
• 干渉条件の導出方法が分からない
• 逆位相のときの干渉条件が分からない
• 干渉条件の使い方が分からない

このような悩みはありませんか？

実は、波の干渉の公式を絶対に間違えない覚え方があるのです。波の干渉条件は経路差が半波長の「偶数倍」なのか「奇数倍」なのかさえ分かれば良いのです。

この記事では、波の干渉の公式の導出と公式の使い方、そして公式の中のmの正体まで明かしていきます。

さらに、逆位相や光路差についても詳しく説明していきます。

この記事を最後まで読むことで、波の干渉条件を間違えることなく使うことができ、今後のヤングの実験や薄膜干渉などの入試頻出である光の干渉の問題を難なく解くことができます。

波の干渉とは？

今回は波の干渉を扱いますので、まずそもそも波の干渉って何か説明しますね。

波の干渉というのは「波の重ね合わせ」ということです。

二つの波が重なることで、別の一つの波ができます。

いろんな重なり方がありますが、特にお互いの波が

• 強め合う場合
• 弱めあう場合

この二つが重要になります。

強めあうというのは、山同士または谷同士が重なりあうことです。これにより、より大きな波ができます。

弱めあうというのは、山と谷が重なり合うことです。これにより、より波が消失します。

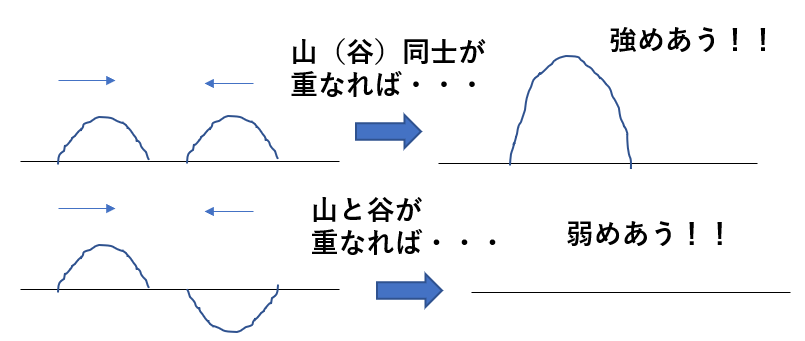
この現象があるので、音を大きくしたり小さくしたり、光を明るくしたり暗くしたりできるのです。

物理を学んでいるみなさんには、これを数式にしなければなりません。

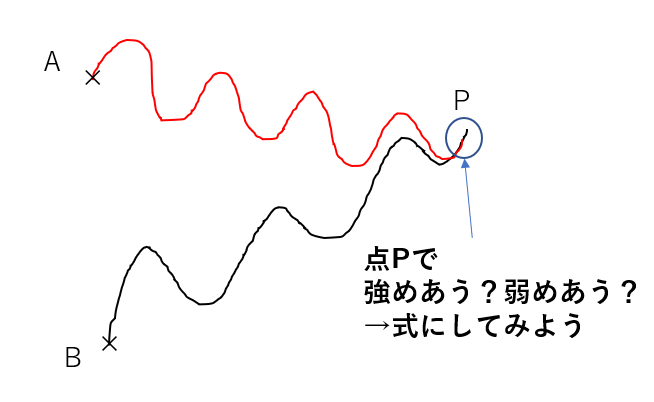
このように、二つの地点A,Bから出た波が点Pで重なったときに、

• 強めあうときはどんな式で表せるのか
• 弱めあうときはどんな式で表せるのか

を考えていきましょう。

波の干渉を考えるときの注意点

これから、強めあう条件と弱めあう条件を公式として表していきたいのですが、ある2つの条件を先に伝えておきます。

1. 2つの波は同位相で始まり、波形は同じである
2. 空気中を進む（同じ媒質中を進む）

1を仮定しておかないと、これから考えるように「経路」だけで判断することができなくなってしまいます。

2を仮定しておかないと、特に光においては波形が変わってしまい、「経路」だけで判断できなくなってしまいます。

まずは簡単な場合を考えるための、このような条件をつけておきます。

（もちろん、この条件が無い場合の干渉も考えていきます。）

強め合う条件を式にしてみよう

まず、強めあう条件を式にしてみましょう。

強め合うというのは、山（谷）同士が重なる場合でしたね。

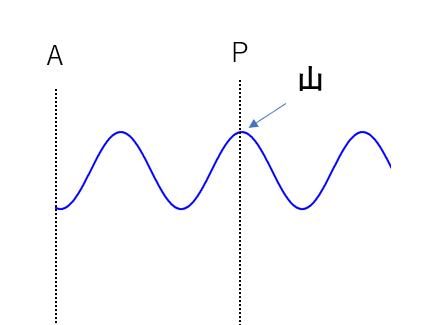
まず、Aから出た波が、図のように点Pに山で到達したとします。

最初に見せた条件1から、Bから出た波は、APの間でAの波と同じ波形をしないと点Pに山で到達することはできません。

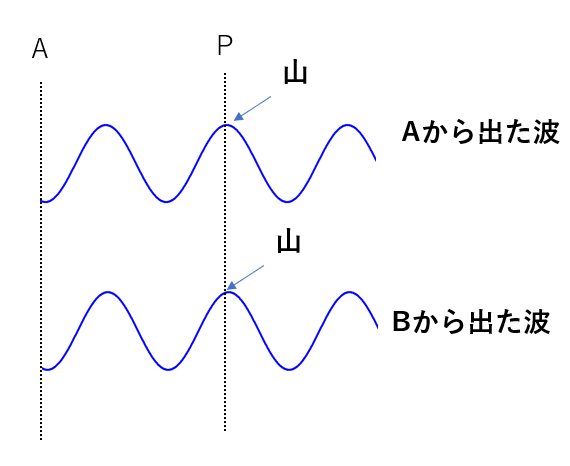
つまりこのようになれば、点Pで山同士が重なるわけですね。

では、この状況が生まれるためには点Bはどこの位置にある必要があるでしょう？

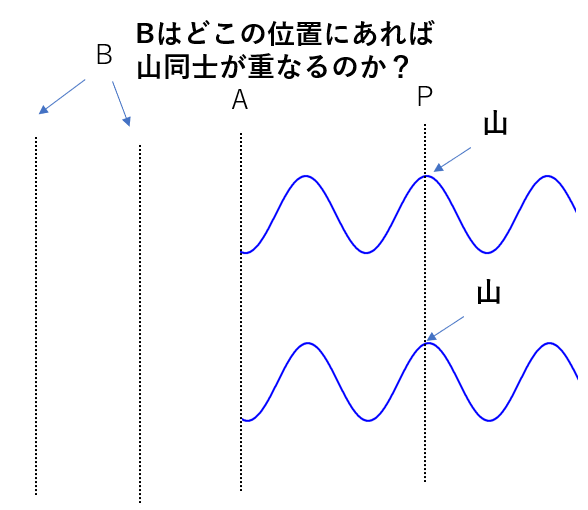
これはどこでも良いわけではありません。条件１があります。

2つの波は同位相で出発しなければいけません。

つまり、Aが山で出発するならBも山で、Aが谷で出発するならBも谷で出発しなければいけないのです。

この図ではAが「谷」で出発しているのでBも「谷」で出発します。

谷となる部分は無限にありますが、そのどれかに点Bを取ることで点Pで強めあうのです。

これを見ると、Bの位置にはある規則性が見えてきます。APとBPの経路差、つまりAB間の距離を見てみましょう。

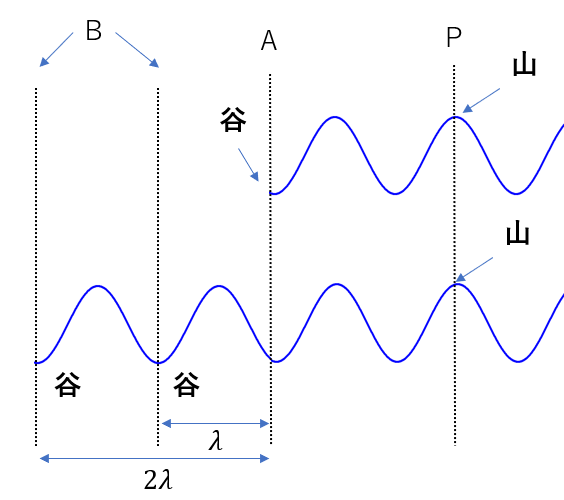
ABの経路の差が$\lambda, 2\lambda...$となってる！

そうです。経路差が**「波長の整数倍」**になっているんですね。

つまり、強め合う条件を式にすると

$(経路差) = m\lambda$
と表せるのです！

強めあう条件は無事式にできました。（ちなみに、この式は絶対に覚えないでください）

弱めあう条件

同じように、今度は弱めあう条件を考えます。

弱めあうというのは山と谷が重なるということでした。

先ほどと同様に、Aから出た波が点Pに山で到達したとしますね。

点Pで弱めあうには、Bから出た波は点Pに谷で到達しなければいけません。

条件1から、Aの波と同じ波形（波長）の波が出ることから、AP間では次の図のような波形しかありえません。

このようになれば、点Pで弱めあいます。

では、点Bはどこにあればいいのでしょう？

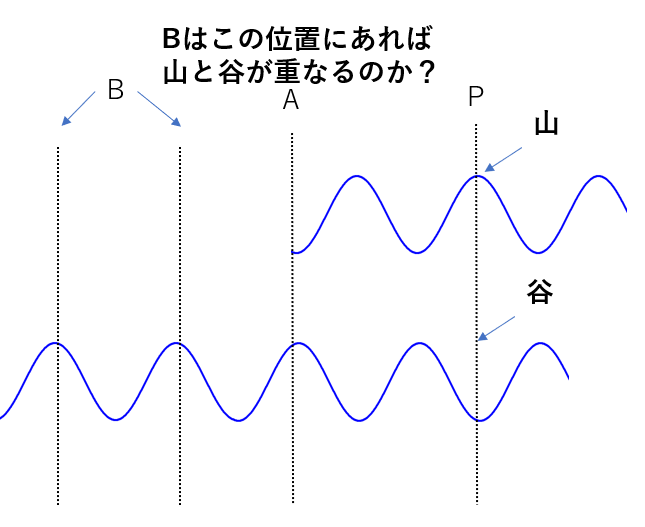
先ほどと同じで、点Aで谷から出発しているので、点Bでも谷から出発しなければいけません。

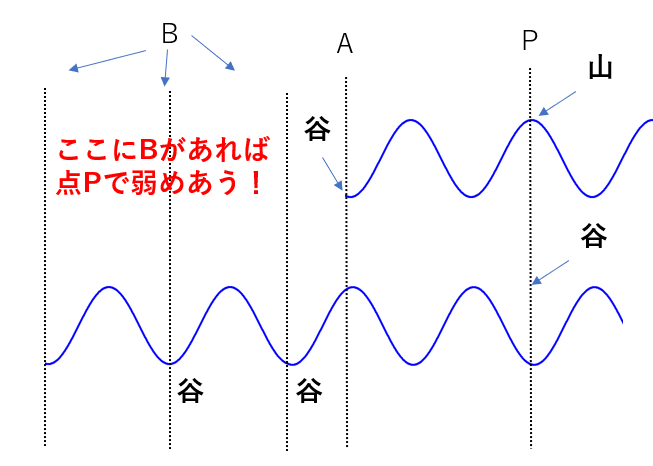
このような位置に点Bがくれば、点Pで波が弱めあうことが分かりますね。

これも先ほどと同じように、二つの波の経路差を考えてみましょう。こちらもある規則性が見えてきます。

ABの経路の差が$(0 + \frac{1}{2})\lambda, (1 + \frac{1}{2})\lambda...$となってる！

つまり、
$(経路差) = (m + \frac{1}{2})\lambda)$
となるときに、弱めあうということが分かりましたね。

（これも覚えないでください）

波の干渉の公式→半波長の「偶数倍」か「奇数倍」

ここまでで、干渉条件の式を導けました。

これは教科書とかでまとめられている形なんですが、覚えにくくて何かと不便ですよね。

なので、式を変形しましょう。

このように見るとどうですか？

$\frac{2}{\lambda}$は波長の半分ということですね。

$2m$は偶数、$2m + 1$は奇数です。

このようにすれば、経路差が半波長の「偶数倍」なのか「奇数倍」なのかで判断できるのです。

これなら公式として覚えやすいですよね。

先ほどの図で、波長単位で経路差を見てきましたが、それを半波長単位で見ることによってこのような式を出すことができますね。

波の干渉の公式

＊これが成り立つ条件

1. 2つの波は同位相で始まり、波形は同じである
2. 空気中を進む（同じ媒質中を進む）

もちろん、これは自分の力で導出した上で「使っているうちに覚えた」という感覚で覚えてください。

暗記しようとは絶対にしないでください。

また、波の干渉の公式が成り立つ条件も必ず押さえておいてください！これはめちゃめちゃ大事です！！

位相がそろっていないとどうなるの？

最初の条件で同位相というものつけました。

この条件はかなり重要でこの条件がないと、「経路差」を考えるだけでは干渉条件が使えなくなります。

先ほどの例を使うと、例えば点Aでは谷から出発しているのに、点Bでは谷でもなく山でもなく、中途半端なところから出るとかなり面倒になります。

こうなってしまうと式に表すのが面倒になってしまいます。

なので経路差が簡単に求められるように、「同位相」という条件を付けたのです。

しかし、位相が違くても特別な場合にのみ、波の干渉条件を式で表すことができます。
それは逆位相のときです。

出発のときに位相が真逆だったら、つまり波形が真逆だったらさっきの干渉条件も逆になります。

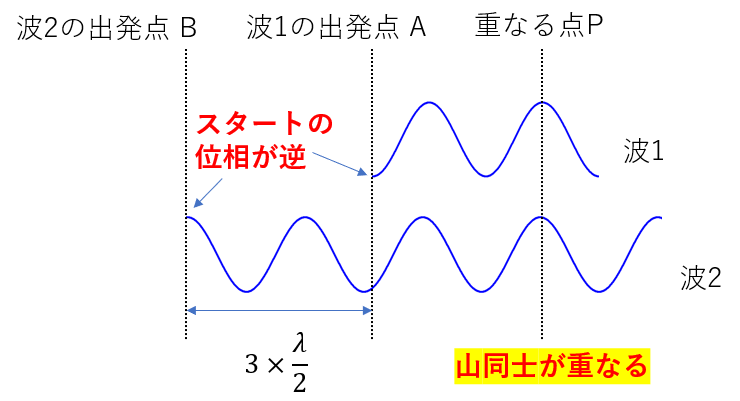
このように、経路差が「半波長の奇数倍」なのに、山同士で重なって強め合ってますね。

同様に、経路差が「半波長の偶数倍」のときは、弱めあいます。

先ほど見せた条件が反転しています。これは光の干渉などで、反射によって位相がずれるときに必要になるので、しっかり理解しておいてください。

• 波が逆位相のとき波の干渉の条件が逆になる

ちなみに、逆位相になることを「位相が$\pi$ずれる」と言います。

問題では見かけませんが、位相が$\frac{\pi}{2}$ずれる場合も干渉の式を出すことはできそうですね。

ここではやりませんが考えてみても良いでしょう。

空気中じゃないとどうなるの？

もう一つの条件2「空気中」というのがありました。

この条件もなかったらどうなるでしょうか？

これもさっきと同じで、位相がずれちゃってうまく式に表せなくなります。

これは光の干渉においてよく出てきます。

波は空気中、水、ガラスなど、進む環境（これを媒質という）によって波長や速さが変わってしまいます。

詳しくは「スネルの法則」を見てください。

https://ryebourbon.xsrv.jp/refraction-light/

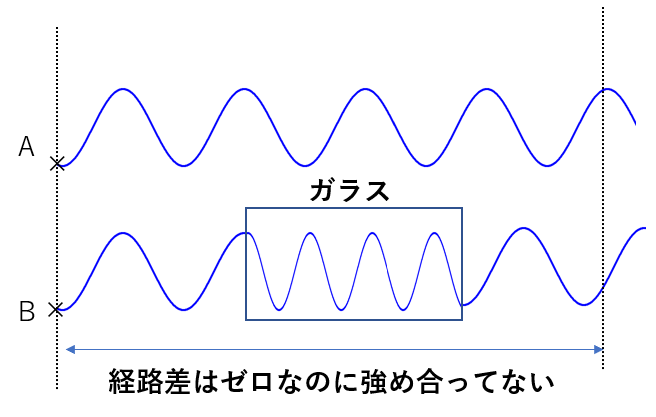
このように、先ほど見せた例なら経路差がなければ当然強め合うはずですが、Bの途中にガラスを置くことで

ガラス中にあるときの波形はAと変わってしまうため強めあわないのです。

この場合、ガラス中にある波を空気中に置き換えないといけません。

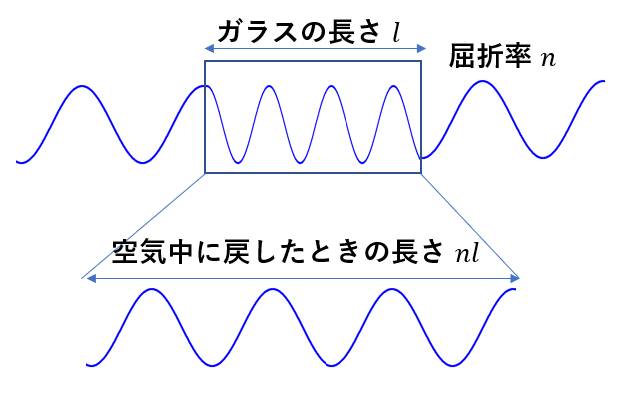
この空気中に戻したときの光の進む距離を「光路長」といいます。

屈折率$n$の媒質の長さが$l$のとき、光路長は$nl$と表すことができます。

このように、すべて空気中にそろえてから経路の差を考える必要があるのです。

その差を「光路差」と言います。

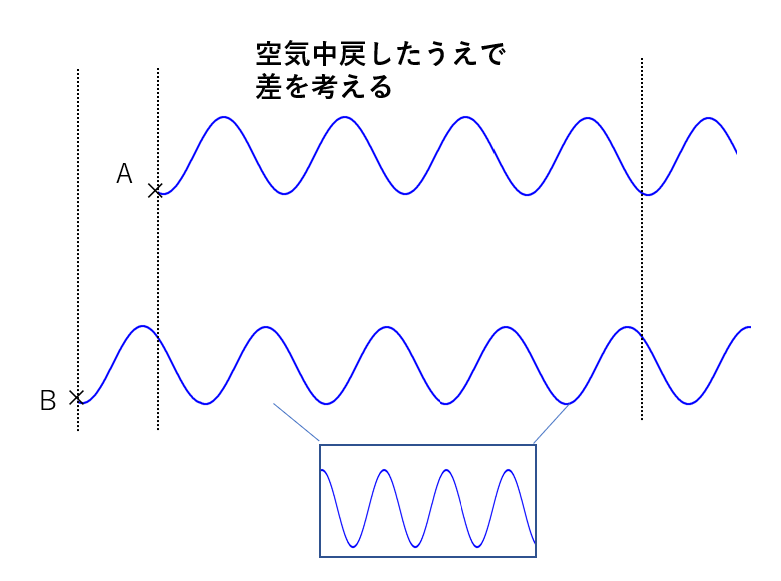
薄膜干渉などでこれが使われていますので、ぜひそちらを確認ください

https://ryebourbon.xsrv.jp/hakumaku/

まとめ：波の干渉の公式はしっかり理解しよう

いかがでしたか？

波の干渉の公式は非常に大事です。光の干渉の問題で絶対に使います。

もちろん式は覚えた方が楽ですし、入試問題は時間が限られている以上、いちいち導出している暇はないと思います。

ですが、公式をただ数式のように暗記するのではなく

導出した上でどのような意味があってまたどんな条件の下で成立してその条件が無くなった場合はどうなるのか

をきっちり理解してください。

これを踏まえて光の干渉を見ていきましょう！

ヤングの干渉実験。聞かれる問題をすべてまとめてみた！薄膜干渉をシャボン玉で理解する！条件式求めて適用せよ！くさび形空気層とニュートンリング。やってること同じじゃん！

波の干渉の公式

＊これが成り立つ条件

1. 2つの波は同位相で始まり、波形は同じである
2. 空気中を進む（同じ媒質中を進む）

＜注意１＞
逆位相の場合→上の干渉条件が逆になる

＜注意２＞
光がガラスや水などの媒質を進むとき→光路差を考える（光路長は$nl$と表せる）