コンデンサーの極板間引力って何？電場とエネルギーの観点から導く
今日はちょっとしたお話（ちょっとしてもないけど）、極板間引力っていうのを考えたいと思うよ！
AKINORI
極板間引力？
AI
コンデンサーのって二つの極板が向かい合っていますよね？
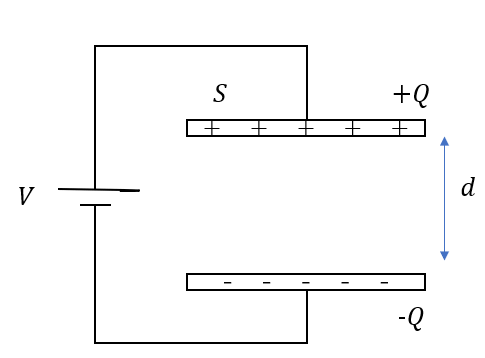
この極板には電荷があるから、この二つの極板が引き合うのはわかりますね。
じゃあ、実際にこの引き合う力「極板間引力」はどれくらいなんでしょう？
ここでは仕事とエネルギーを使って考えたいと思います！！
また微小量を扱う練習にもなるので、ぜひ読んでいってね！！
例題で考えよう！極板間引力
電気量がQのコンデンサーを考える。今、極板間距離がdであり、互いに大きさFの力が働いている。極板Aを微小距離\Delta dだけ動かすことを考える。極板の面積をS,真空の誘電率を\varepsilon_0とし、極板はゆっくり動かすとする。
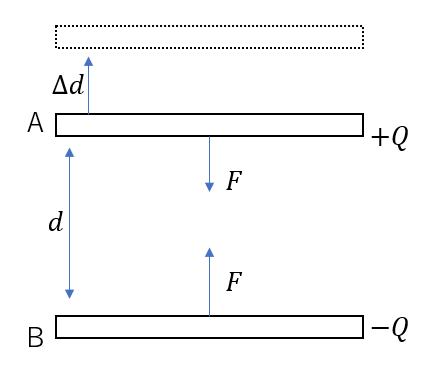
(1) 外力がする仕事\Delta Wを求めよ
(2) 引き離す前後の静電エネルギーU, U’を求めよ
(3) Fを求めよ。
（１）キーワードは「微小」
（１）では微小量の扱いが重要なんだ
AKINORI
微小量の扱い？
AI
そう。微小を考えることで本来変化するものを一定に考えることができるんだ！
AKINORI
微小量の扱いについてはコンデンサーの静電エネルギーでもやっています。ぜひご覧あれ！
極板をゆっくり動かすから、
力はつり合いを保つ
つまり、極板を動かす外力の大きさもFということです。
極板間引力ってようは静電気力だから距離によって変化しそうですよね？
ですから、仕事を考えるときに、「力×距離」と表すことができないんです。
でも、微小距離だったら？
ほんのちょっとしか動かないから、この区間での力は一定とみなして良いですよね。
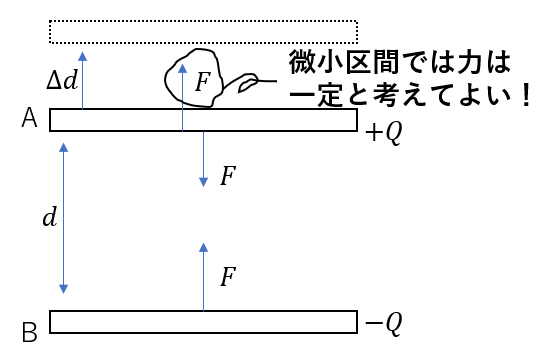
なので、仕事を求めやすくなるんです。
（まあ、結論を言うと今回はFは常に一定なので、微小を考えなくてもいいんですが・・・）
ということで、外力がする仕事は
\Delta W = F\Delta d
です。
（２）「電荷」は一定
これはU = \frac{1}{2}CV^2を使えばいいんですね。
AI
そうだね。ただ、これは必要に応じてQ = CVを使って変形しないといけないことに注意ね。
AKINORI
静電エネルギーについては「【物理】コンデンサーの公式ってどう導く？コンデンサーの性質大公開！」をチェック！
今回、Vは求められないですね。
ただ\varepsilon_0や極板間距離d、そして面積Sがあるから、電気容量Cは使えそうです。
さらに、今回、極板は完全に独立してますよね？「島」です。
ですから、電荷が移動できないわけです。
つまり、極板を動かそうが、電荷量は
Qで一定！！
ということでU = \frac{1}{2}QVをQ = CVを使って、Q, Cの式で表すと
U = \frac{Q^2}{2C}
これを使っていきましょう。
まず、電気容量を求めますね。
電気容量は
C = \varepsilon_0 \frac{S}{d}
でした。
- 面積が大きいほど
- 距離が小さいほど
電気容量は大きくなるんでした！！
まず、引き離す前ではこのCが電気容量ですね。
そして、引き離した後は、距離がd + \Delta dとなるので
引き離したあとの電気容量C’は
C’ = \varepsilon_0 \frac{S}{d + \Delta d}
です
あとは静電エネルギーを式に入れて出すだけですね。
U = \frac{dQ^2}{2\varepsilon_0 S}
U’ = \frac{(d + \Delta d) Q^2}{2\varepsilon_0 S}
これが（２）の答えです！！
（３）これはもうエネルギー保存則でしょ！！
仕事、エネルギーと求めたらもうやるべきことは・・・
AKINORI
エネルギー保存則ですね！
AI
エネルギー保存則についてはこちらで！！
エネルギー保存則っていうのは
（はじめの力学的エネルギー）＋（非保存力にされた仕事）＝（あとの力学的エネルギー）
これでしたね。
仕事をされればエネルギーが変化する
っていうのが簡単なイメージでしたね。
静電エネルギーっていうのは極板がもつ一種の位置にエネルギーです。
（静電気力（保存力）を受けているからイメージ付くかな？）
ゆっくり動かすのでもちろん運動エネルギーはゼロですね。
というわけで、当てはめていくと
U + \Delta W = U’
F = \frac{Q^2}{2\varepsilon_0 S}
これが答えになります。
極板間引力の特徴
よく見るとFは定数ですよね。距離に依りませんね。
つまり、極板間引力はどこでも一定です。
といっても、これは当たり前で、
平行に極板を向かい合わせると、電場って一様にできますよね。
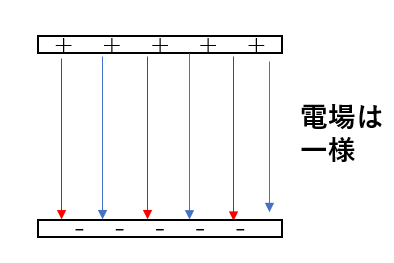
電場が一様だったら静電気力も一様ですよね。
だから、この結果は当たり前っちゃ当たり前です。
それともう一つ。
「【物理】コンデンサーの公式ってどう導く？コンデンサーの性質大公開！」
でもやりました。
一つの極板による電場の大きさっていくつでしたっけ？
E_0 = \frac{Q}{2\varepsilon_0 S}
でしたよね。ガウスの法則ので求めました。
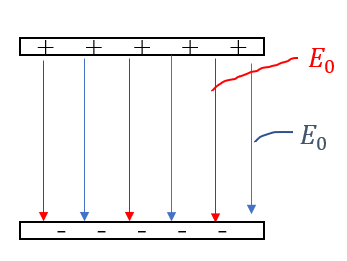
下の極板は上の極板が作る赤色の電場によって力を受けます。
このとき、下の極板が作る作る青色の電場は無関係ですよね？
だってこれは下の極板が作っているんですもの。
自分自身がつくる電場によって自分は静電気力は受けないです。
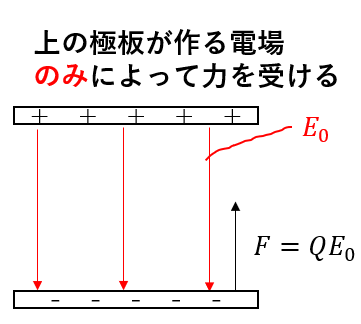
ということで下側の極板が受ける力は
F = QE_0
です。
上の極板も同じようにF = QE_0の大きさの力を受けます。
さて、E_0を具体的に入れてみると
F = \frac{Q^2}{2\varepsilon_0 S}
あ！例題で求めたやつと一緒だ！
AI
そりゃそうですよね。二つの電荷が引き合っている静電気力が極板間引力なんだから。
AKINORI
E_0は片側の極板が作る電場なので、実際には極板間に生じる電場はE = 2E_0です。
なので、極板間に生じる電場Eを使って考えると
F = \frac{1}{2}QE
となりますね。
あ！私、いきなりこの式が問題集の解説に書かれていてずっと「なんで？」って思っていたんですが、こういうことだったんですね！！納得！
AI
まとめ
AIさんのように、たまに極板間引力をF = \frac{1}{2}QEといきなり出されることがあるんですが、こうやってしっかり導けばそんなのあたりまえなんですね。
「なんで？」って思ったら自分で式を導いてみることは重要です。
極板間引力は「電場」と「エネルギー」という二つの観点から導けることが分かりましたね。どちらでも説明できるように理解しておいてください！！
今回は微小量から極板間引力をやってみました。ぜひ、微小量の扱いにも慣れておいてくださいね！！
極板間引力に関連した記事もチェック！！
