定常波にも式があった?式からわかる腹や節の位置

Akinoriさん。正弦波は式で書けましたよね。
 AI
AI
そうだね。いつでも導出できるようにするんでしたね。
 AKINORI
AKINORI
なら、定常波にも式ってあるんですか??
 AI
AI
あるよ!!実際に使えるかというと、あまり使えないけど、知っておくと理解が深まるよ。
 AKINORI
AKINORI
定常波っていうやつはこんなやつです。
二つの波を重ねたとき、
停滞するような波ができることがある。
これが定常波です。
定常波は節と腹の位置が固定されている
みたいな性質があるんですが、それを今回は式で見てみよう!!
というのがテーマです。
波を重ね合わせると
定常波は波を重ね合わせないと起こりません。
じゃあ、波を重ね合わせるとどうなるんでしょう?
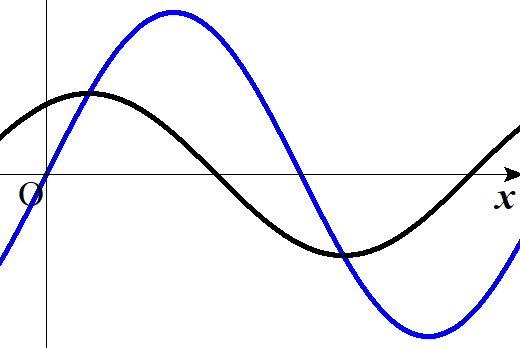
今、図のような二つの波があります。
この波は重なっていますね。
実際にはこうやって見えず、一つの波として目に見えます。
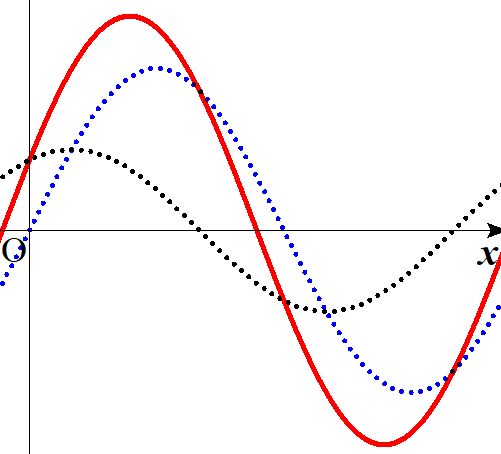
実際には、赤の実線の波が見えるわけです。
この赤の波を合成波と言います。
この波の高さはこうやって表せます。

ある点で見ると、単純に高さを足すだけです。
\(y_3 = y_1 + y_2\)
これで、赤の波のある点の高さが出ます。
波全体(波の形状)も式を足せば出ます。
ただ足すだけで合成できるってことなんですね。
 AI
AI
これを波の重ね合わせの原理とかいう、無駄にカッコいい名前がついてます(笑)。
 AKINORI
AKINORI
似た者同士を足してみる
では、今回は形がよく似た二つの波を重ね合わせてみます。
結論からいうと、この合成波が定常波になります。
\(y = A\sin{\omega (t – \frac{x}{v})}\)、\(y = A\sin{\omega (t + \frac{x}{v})}\)と表された二つの正弦波がある。これが重なったときにできる合成波を式で表せ。
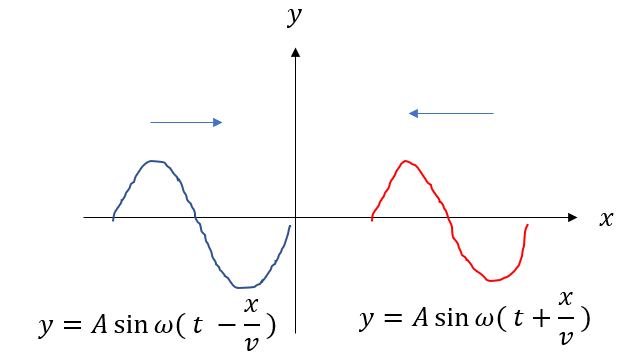
正弦波の式についてはこちらをチェック!!
この二つの波は互いに逆向きに進んでいるので重なります。
合成波はこの二つの波の式を足せば出てきます。
とりあえず足してみましょう。
\(y = A\sin{\omega (t + \frac{x}{v})} + A\sin{\omega (t – \frac{x}{v})}\)
う~ん。これ以上変形できなさそうです・・・
 AI
AI
ちょっと応用的になるんだけど、三角関数の和積公式を使ってあげるともっときれいに書けるよ。
 AKINORI
AKINORI
ここからは数学です。
この公式(?)を知っていますか。
\(\sin{\alpha} + \sin{\beta} = 2\sin{\frac{\alpha + \beta}{2}}\cos{\frac{\alpha – \beta}{2}}\)
数Ⅱの三角関数のところで出てきたと思います。
僕は「シン足すシンはニシンの子」
って覚えています。
これを使います。
途中式は面倒なので省略しますが、計算すると
\(y = 2A\sin (\omega t) \cos{(\frac{\omega}{v}x)}\)
こんな形になります。
このsinやcosの中身が\(t, x\)でそれぞれ分かれているところが重要です。
 AKINORI
AKINORI
この式を眺めてみましょう。
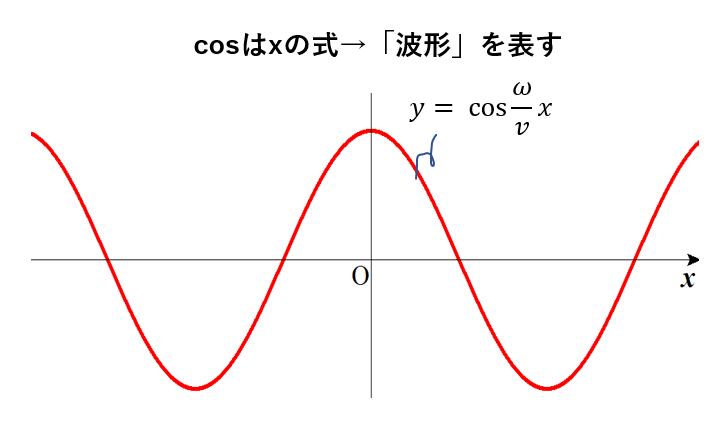
まず、後ろのcosの部分。
これは、
\(x\)のみの式になっていますよね。
つまり、位置に関するcosの式ということです。
これはいわゆる、「波形」を表します。
そして、sinの部分。
これは
\(t\)のみの式になっていますね
つまり、時間に関するsinの式ということです。
sinは-1から1の値を取ります。
これがcosの係数となっているので、これは「波の振幅」を表しています。
時間で変化するってことは、高さが時間で変わっていくってことです。
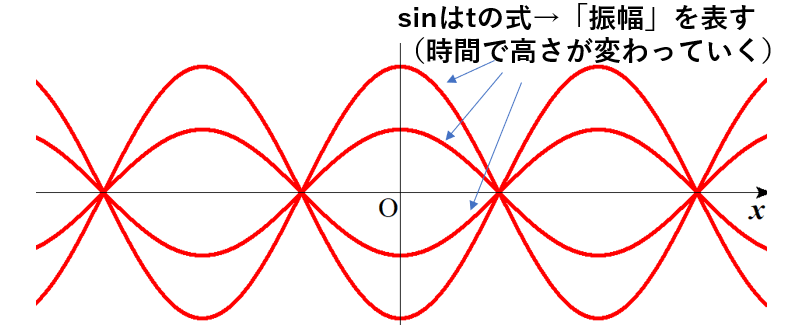
大まかな波形は変えず、高さのみが変化していく。
あ!これ定常波です!!
 AI
AI
そう。x,tが独立すると定常波になるんだ。
 AKINORI
AKINORI
はじめの正弦波の式では、
\(y = A\sin{\omega (t – \frac{x}{v})}\)
このようにsinの中に\(t, x\)の両方が含まれています。ですからsinの値は\(t,x\)の両方が関係してきます。
一方、さっきの合成波の式は
\(y = 2A\sin (\omega t) \cos{(\frac{\omega}{v}x)}\)
このように、sinやcosの中身が\(t\)のみであったり\(x\)のみであったりしますね。
さっきはこの二つが影響しあっていたけど、今度は独立しています。
この独立している場合が定常波になるんです。
- 定常波の式
\(y = (tのみの三角関数)×(xのみの三角関数)\)
定常波には式としてそんな性質があるんですね。良いこと知った!
 AI
AI
式から見た定常波の性質
この式から定常波の性質を見ることができます。
 AKINORI
AKINORI
定常波と言えば
節や腹の位置
ですよね。
これをさっき求めた式を使って考えましょう。
節について
まずは節です。
節って何かというと
全く振動しない点
のことです。
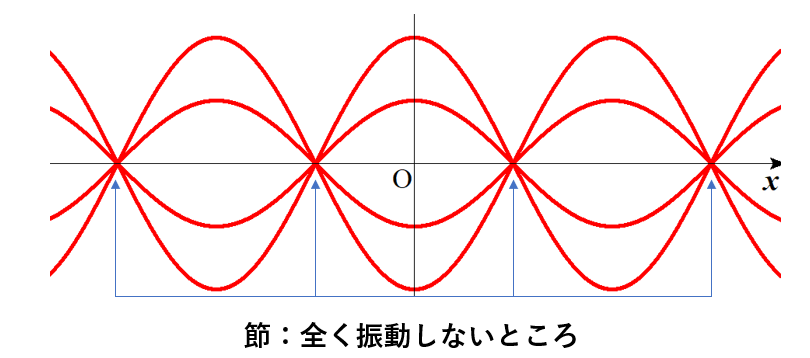
全く振動しないということは
どんな時刻\(t\)でも常に\(y = 0\)ということです。
さて、定常波の式を見てください。
\(y = 2A\sin (\omega t) \cos{(\frac{\omega}{v}x)}\)
これが\(t\)に関係なく常に\(y = 0\)であればいいんです。
そのためにはcosの部分が0になっていればいいですね。
\(\cos{(\frac{\omega }{v}x)} = 0\)
普通に数学でやるように解いてみると
\(\frac{\omega}{v}x = \frac{\pi}{2} + n\pi\)
ですね。
ここで、
\(\omega = \frac{2\pi}{T} = 2\pi f\)
と表せます。
また、波の基本式\(v = f\lambda\)を使えば
\(\frac{f}{v} = \frac{1}{\lambda}\)
です。
なので、式を変形すると
\(\frac{2\pi}{\lambda}x = \frac{\pi}{2} + n\pi\)
∴\(x = \frac{2n + 1}{4}\lambda\)
これが節の位置ということです。
隣り合う節の間隔、つまりn番目とn + 1番目の間隔\(\Delta x\)を見てみると
\(\Delta x = \frac{2(n + 1) + 1}{4}\lambda – \frac{2n + 1}{4}\lambda\)
∴\(\Delta x = \frac{\lambda}{2}\)
あ!間隔が\(\frac{\lambda}{2}\)!!これよく知ってる!
 AI
AI
そう。節が半波長ずつ並ぶという性質がわかったね
 AKINORI
AKINORI
腹について
腹は何かというと
一番振動している点
のことです。
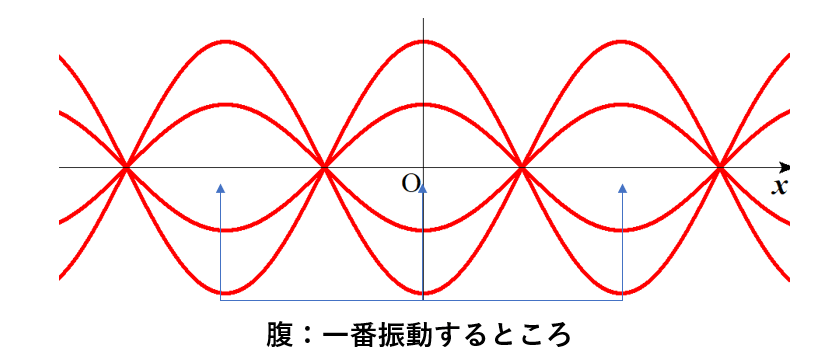
一番振動するってことはある時間\(t\)で最大振幅が\(2A\)になっているような点のことです。
そのためにはcosが1や-1を取らないと\(2A\)になりませんね。
\(\cos{(\frac{\omega }{v}x)} = \pm 1\)
∴\(\frac{\omega}{v}x = n\pi\)
さっきと同じように解くと
\(x = \frac{n}{2}\lambda\)
隣り合う腹の間隔、つまりnとn+1番目の間隔\(\Delta x\)は
\(\Delta x = \frac{n + 1}{2}\lambda – \frac{n}{2}\lambda\)
∴\(\Delta x = \frac{\lambda}{2}\)
これも知ってるやつです!!
 AI
AI
節と同様で、腹の間隔も半波長なんですね。
 AKINORI
AKINORI
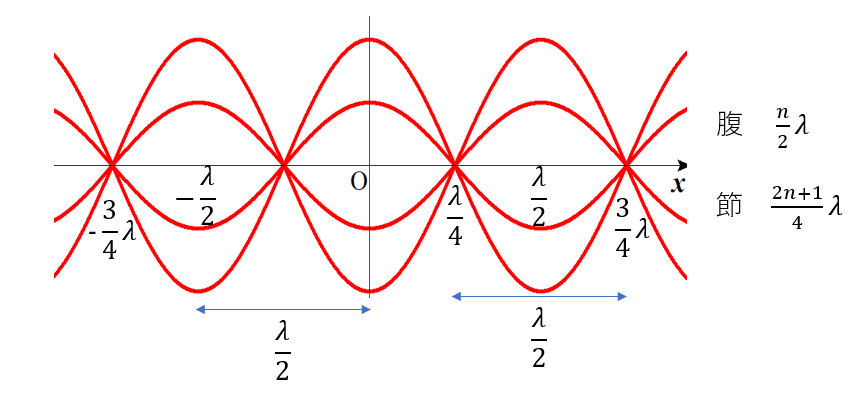
こうやって式から定常波の性質を理解することができます。
こういう式から理解する
というのも重要なスキルなので、ぜひ習得してみてください!!
まとめ
- 定常波の式
\(y = (tのみの三角関数)×(xのみの三角関数)\)
- 定常波の性質
節の間隔、腹の間隔は\(\frac{\lambda}{2}\)









Comment
この式の語呂合わせを考えました。
2cos(ωx/v)×Asin(ωt)として、
「二個目がくすぶりアシンメトリー」です。