電磁気の公式を総まとめしてみた!

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
今回は、電磁気で出てくる公式を総まとめしました。
公式の注意点や使い方を一気に知りたいという要望にこたえました。
公式の意味はもちろんのこと、問題での便利な使い方も解説していますので、この1ページで公式を網羅しましょう!
とはいえ、ただ暗記はやめてくださいね。
公式にある背景もしっかり理解した上でこのページを利用することをオススメします。
目次
静電気力と電場
電気量\(q_1, q_2\)の電荷が距離\(r\)だけ離れているとき、互いはたらく静電気力の大きさは次のように表せる
\(F = k\frac{q_1 q_2}{r^2}\)
- 同符号のとき反発する向き
- 異符号のときに引き合う向き
点電荷\(q_1\)が距離\(r\)の位置に作る電場の大きさは次のように表せる
\(E=k\frac{q_1}{r^2}\)
静電気力と電場のポイント
公式をしっかり覚えればこの辺は特に難しくありません。
電場の式は静電気力において\(q_2 =1\)とした場合の式に一致します。
つまり、+1Cの電荷が受ける静電気力に等しいのです。
なので、電場を扱う場合は+1[C]の電荷を置いて考えると良いですね。
ガウスの法則
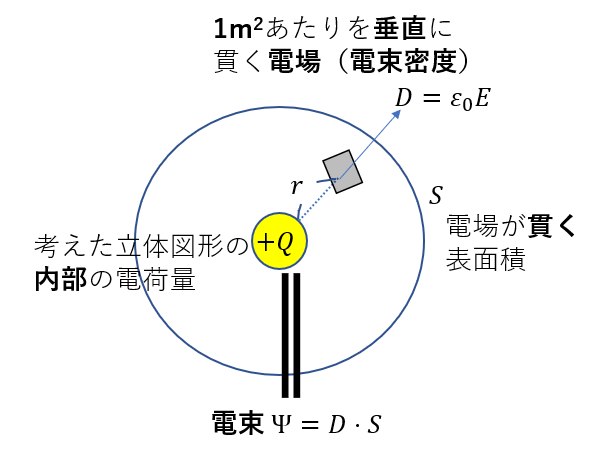
ある立体領域の内部に総和\(Q\)の電気量があるとき、立体の表面積を\(S\)、1m2あたりを垂直に貫く電場を大きさを\(E\)とすると次のような関係が得られる。
\(DS = Q\) (\(D\)=\(\varepsilon_0 E\)
ガウスの法則のポイント
ポイントは電荷の形状に合わせて、立体図形を決めることです。
領域を垂直に貫く電場を考える必要があるので、電荷から生じる電場がどの面でも垂直になるように図形を考える必要があります。
また、電荷\(Q\)ですが、これは立体内部のみの電荷を考えます。そして、立体内部にある電荷は正負を含めてすべて足したものが式に使われます。

コンデンサー
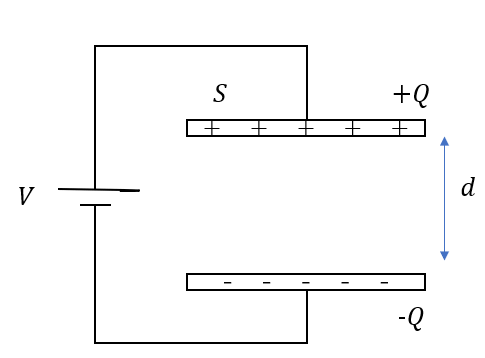
コンデンサーの電位差を\(V\)、電気容量を\(C\)とすると、コンデンサーに蓄えられる電気量\(Q\)は次のように表せる。
\(Q = CV\)
また極板間隔を\(d\)、断面積を\(S\)とすると電気容量\(C\)は次のように表せる。
\(C = \varepsilo_0 \frac{S}{d}\)
コンデンサーのポイント
コンデンサーの公式をしっかり覚えればOKです。
大事なのはコンデンサーの扱い方ですね。
コンデンサーが回路にあるときは以下2点に注意しましょう。
電気量保存則
→「島」を見つける
スイッチ操作
・スイッチを入れた直後→導線扱い
・スイッチを入れて十分時間経過→断線
コンデンサーは極板に間隔があるため、回路内で独立する部分が出てきます。その中では電荷の出入りがないため、総和は常に一定になります。これが電荷保存則です。
また、スイッチ操作も重要です。
電荷がない状態でスイッチをとじると、その直後はまだ電荷が蓄えられないので導線扱いになります。
十分に時間が経過すると、電荷が最大に蓄えられるので、断線扱いになります。
抵抗と直流回路
オームの法則;\(V = RI\)
電流の式:\(I = vSne\)
キルヒホッフの法則
・流れ込む電流=流れ出る電流
・一周した電位=0
抵抗と直流回路のポイント
ポイントはキルヒホッフの法則です。
これはコンデンサーが含まれようと、ダイオードが含まれようと、交流回路であろうと必ず使います。
以下のステップを必ず踏んで回路問題は解くようにしましょう。
- 電圧マークをつける
- 閉回路を一周する
1周する際に、電圧マークが大きくなる向きに進めばプラス、逆向きならマイナスをつけて足していきます。
磁場
磁荷\(q_1, q_2\)が、距離\(r\)離れているときに働く磁気力は
\(F = k\frac{q_1 q_2}{r^2}\)
また、磁荷\(q_1\)の磁荷が作る磁場は
\(H = k\frac{q_1}{r^2}\)
電流が作る磁場
・直線電流 \(H = \frac{I}{2\pi r}\)
・円形電流 \(H = \frac{I}{2r}\)
・ソレノイド \(H = nI\)(\(n\)は単位長さ当たりの巻き数)
磁場のポイント
ポイントは特にありません。公式は高校生では導出不可能なので暗記してください。
あまり出ませんが、ソレノイドはたま~に出てくるのでソレノイドは絶対に忘れてはいけませんよ。
特に\(H = nI\)の\(n\)は単位長さ当たりの巻き数なので注意てください。
電磁誘導
巻き数\(N\)のコイルを貫く磁束が時間\(\Delta t\)の間に\(\Delta \Phi\)変化するとき誘導起電力は
\(V = -N\frac{\Delta Phi}{\Delta t}\)
*向きはレンツの法則にしたがう
電磁誘導のポイント
電磁誘導はこの公式を正確に使えるかどうかが重要です。
磁束は垂直に貫くものを考える必要があったり、誘導起電力の向きには注意が必要です。
式ではマイナスがついた形になっていますが、このままダイレクトに計算すると混乱します。
なので、まずは大きさだけを求めて、そのあとに向きをレンツの法則から決定するといいでしょう。
磁束の変化を妨げるように起電力ははたらきます。
交流回路
各素子のリアクタンス
・抵抗:\(R\)
・コイル:\(\omega L\)
・コンデンサー:\(\frac{1}{\omega C}\)
交流回路のポイント
交流回路で重要なことは交流回路の理解を深めることです。暗記して小手先の技術で解けるようなものではありません。
交流は日常生活と大きくかかわっています。なので、日常生活とリンクさせて理解を深めるのがベストです。
「交流だと計算が難しいから、直流に置き換える」
この考え方を身に付ければ簡単に交流が理解できます。
交流を直流に置き換えた電流と電圧が実効値であり、交流を直流に置き換えたときコイルやコンデンサーを抵抗と同じ役割を持ち、その抵抗値がリアクタンスというわけです。
それさえ分かっていれば、交流回路の理解はできたも同然です。
あとは直流回路と同じように、キルヒホッフの法則を使って考えればOKですね。















