交流って何?交流電流を発生させる方法を解説!

交流とは
いままで扱ってきたのは直流です。直流電流、直流電圧を扱ってきたんだ。
直流はいわゆる電池です。常に同じ起電力を持ち、常に同じ電流が流れるんだ。
これに対し日常で送られている電気は交流です。コンセントをさして電気を使うときもすべて交流なんですね。
交流は電圧や電流が時間で常に変化しているんだ。それでここでは「交流」を扱っていこう。
交流の発生
まずはどうやって交流を発生し、どんな式になるかを考えよう。
っていっても特に変わったことはしないんですよ。今までやってきたことを使うだけ。
起電力を発生させる方法って二つしかないんだ。
1 電池を使う
2 電磁誘導
ってことで電磁誘導させればいいね。↓電磁誘導についてはこちら↓
[blogcard url=”https://ryebourbon.xsrv.jp/electromagnetic-induction/”]
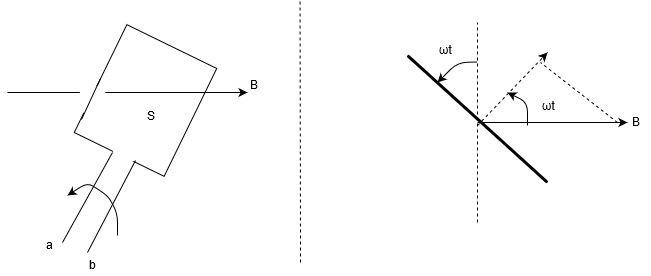
1巻コイルを一定の角速度\(\omega\)で回転させてみよう。初めは磁場に対して垂直にコイルの面がたっているとしよう。
いつも通り磁束変化を考えよう。
ここで、一つ補足(重要)
今まで気にしていなかったけど、厳密にいうとこの磁束は「面に対して垂直」のものが適用されるんだ。
はじめの状態では、面と磁束が垂直なので磁束は\(BS\)でいいだけど、回転すると磁束は面に対して斜めになっちゃうんだ。
斜めになったときは分解して、面に垂直のものだけを考えるんだね。
時刻\(t\)の時、図のように\(\omega t\)だけ回転する。面に対して垂直な磁束密度は\(B\cos{\omega t}\)だ、なので面に垂直な磁束は
\(\Phi = B\cos{\omega t}・S\)
ここで\(\Phi_0 =BS\)(つまり磁束の最大値)と置いて
\(\Phi = \Phi_0\cos{\omega t}\)
で、磁束の変化が何に依存するかっていうのを考える。
変化しているのは時間なので\(\Delta \Phi = \Phi_0\cos{\omega \Delta t}\)としたいところなんだけどこれはダメ。\(t\)てcosの中に入っているよね。だから、時間が変化するとcos自体が変化するんだ。
例えば\(\omega t = 0, \omega t = \frac{\pi}{3}\)の時でそれぞれ、cosの値は\(1, \frac{1}{2}\)だよね。だから、磁束はcosの変化に依存するんだ。
\(\Delta \Phi = \Phi_0 \Delta \cos{\omega t}\)
んで、電磁誘導の大きさは
\(|V| = \Phi_0 \frac{\Delta \Phi}{\Delta t} = \Phi_0 \frac{\Delta \cos{\omega t}}{\Delta t}\)
いったん、ここで向きを考えておく。
図のbを基準に取ると、はじめは右向きの磁束が減るから、それを補うために電流がb→aの向きに流れる。つまり高電位もaである。\(\Delta \Phi<0\)なので、aが高電位(つまり正)になるにはマイナスをかける必要がある。
この関係はずっと同じなので結局、
\(V = -\Phi_0 \frac{\Delta \cos{\omega t}}{\Delta t}\)
高校生はここまで立てられればとりあえずは良いんだけど、この先の話も理解してほしい。
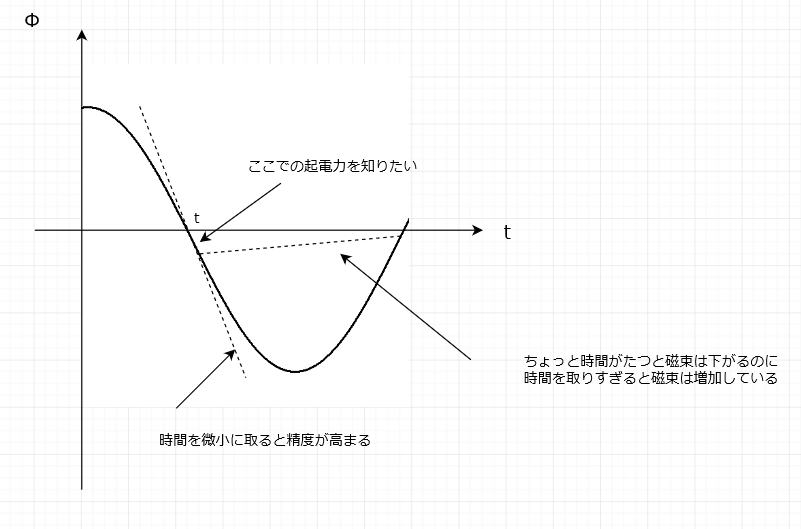
起電力ってある時間一瞬について知りたいんだよ。時間を大きくとりすぎると精度が下がるんだね。
例えば、図の時刻\(t\)での起電力を知りたいとしよう。
この\(t\)から少し時間がたつとグラフから磁束って下がっていくよね。だからこのちょっとの時間では\(\Delta \Phi<0\)でないといけない。
なんだけど、時間を取りすぎると図のように磁束が増えてしまうんだ(\(\Delta \Phi >0\))。明らかに間違いだよね。つまり、厳密に調べるには時間を小さくとる、\(\Delta t \to 0\)を考えないといけないんだ。
数Ⅲをやっている人はわかると思うけど、これって微分だよね。
つまり\(\cos{\omega t}\)を\(t\)で微分すればいいんだ。
\(V = -\Phi_0 \frac{d}{dt}\cos{\omega t} = \omega \Phi_0 \sin{\omega t}\)(合成関数の微分)
\(\omega \Phi_0 = V_0\)(つまり起電力の最大値)とすれば
\(V = V_0\sin{\omega t}\)
これが交流電圧だ。
\(t\)が変化すればsinが変化するから、起電力も変化しているよね。起電力がマイナスにもなったりするんだ。大きさだけでなく、向きも変化するってことも頭に入れておいてね。
まあ、式をみてわかると思うけど、単振動の一種だ。なので周期や振動数も同じ関係がある
\(T = \frac{2\pi}{\omega} , f = \frac{1}{T}\)
とまあ、長々やってきたけど問題で交流電圧の式はちゃんと与えられるから安心してね。微分も導出の時にしか使わないから安心してください。