位相がずれる、リアクタンスってどゆこと?交流回路のコイルを徹底解説

・交流回路でのコイルの性質が分かる
・リアクタンスの意味が分かる
こんにちは。
とにかく電磁気では回路問題は確実に解けるようにしてください。頻出です。
回路問題でやることは決まっていて、
・キルヒホッフの法則
・抵抗、コンデンサ、コイルの性質
この二つをさえ覚えておけば楽勝です。(マジです)
直流の回路に関しては別の記事でやっておりますので、ここでは交流について話をしていきます
ここではコイルの性質についてみていきます。
位相がずれるってなんやねん!
リアクタンスってどういうやつやねん!
という疑問もしっかり解決できますので最後まで読んでくださいね。
(↓コンデンサー、コイルはそれぞれこちらで確認!↓)
交流回路におけるコイル
交流回路では以下の二つを見ていきます
・電流と電圧の関係
・直流回路への変換
これは抵抗でも、コンデンサーでも同じです。
図のように、電圧が\(V = V_0\sin{\omega t}\)の交流電圧にコイルを取り付ける。この時のコイルの性質について考えてみよう
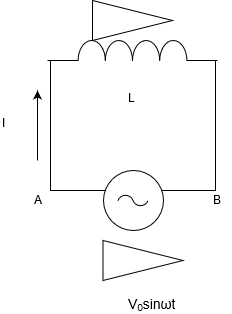
電流はどう表せる?
では、まず最初に電流について考えていきましょう。
ここでは2通りの導き方を教えていきます。(片方は積分を使うのでわからない人は飛ばしてOKです。)
- 積分を使った考え方
電流が増加する場合のみを仮定するとコイルの自己誘導起電力の大きさは
\(|V_L| = L\frac{\Delta I}{\Delta t}\)
です。(わからない人はこちら)
つづいて向きですが、右向きの電流が増加するので、これを妨げるる左向きに電流を流そうとします。なので、誘導起電力の向きは左向きになります。
「一周した電位=0」なので、Bから時計回りに一周すれば、
\(V – V_L = 0\)
∴\(\frac{\Delta I}{\Delta t} = \frac{V_0}{L}\sin{\omega t}\)
もちろん、時間の取り方に依存しないよう、\(\Delta t \to 0\)を考えると、この式は・・・
\(\frac{dI}{dt} = \frac{V_0}{L}\sin{\omega t}\)
と微分方程式となります。微分方程式は高校生の学習範囲外ですので、もちろん解けなくても良いですが、実は皆さんの知識でも解けます。
この式の意味は
「\(I\)を\(t\)で微分したもの=右辺」
です。
つまり右辺を積分したら・・・\(I\)に戻りますよね。
「微分⇄積分」ですから。
ということで、右辺を積分します。
\(I = \frac{V_0}{L} \int \sin{\omega t} dt\)
数Ⅲをやっている人皆さんならもちろん解けますね。
\(I = -\frac{V_0}{\omega L}\cos{\omega t}\)
これでOKですが、この先の説明のためにもう少し式を変形します。
\(\sin{(\omega t – \frac{\pi}{2})} = -\cos{\omega t}\)なので
\(I = \frac{V_0}{\omega L}\sin{(\omega t – \frac{\pi}{2})}\)
積分を使うとこのように電流を導けます(もちろん\(t\)の式になってますね)
- あらかじめ\(I\)を推定する
もう一つの方法を教えます。ここでも図の向きに電流が大きくなる状況を考えます。
ここでは、さっきと違ってはじめに\(I\)の式を予測します。実は少し考えれば予測が可能なんです。
コイルって誘導起電力によって電流に逆らうように働くんですよね。
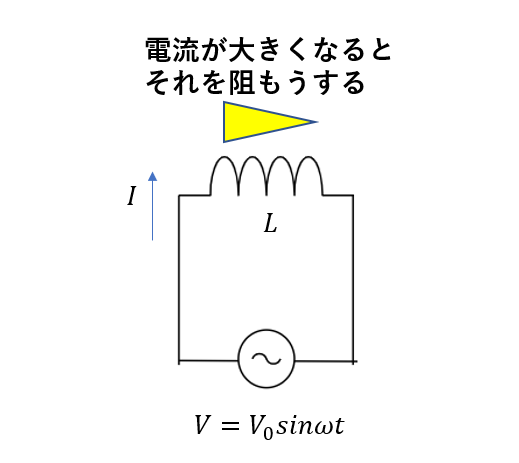
ってことは、電圧とは変化の仕方が変わってきそうじゃないですか?
電圧が0から1になっても、コイルのせいで電流はまだ0の状態。そんなイメージができませんか?
そうすると電圧と電流は時間的に同じように変化しなくなります。つまり位相がずれるわけです。
位相というのは、簡単に言うと変化の仕方のことです。電圧が最大値(最小値)を取るとき、電流も最大値(最小値)を取るなら位相が同じで、撮らない場合は位相がずれているとなります。
特に位相はsinやcosの中身のことを表しますから、電圧の\(\omega t\)よりもいくらかずれた分を考慮して
\(I = I_0\sin{(\omega t + \phi)}\)
と予想できるわけです。すると自己誘導起電力の大きさは
\(V_L = L\frac{\Delta I}{\Delta t} = LI_0\frac{\Delta \sin{(\omega t + \phi)}}{\Delta t}\)
\(\Delta t \to 0\)を考えると、右辺は
\(LI_0 \frac{d\sin{\omega t + \phi}}{dt}\)
つまり\(\sin{\omega t + \phi}\)を\(t\)で微分すればOKです。
\(V_L = \omega LI_0 \cos{\omega t + \phi}\)
あとは「一周した電位=0」を使って、\(V = V_L\)なので
\(V_0\sin{\omega t} = \omega L I_0\cos{(\omega t + \phi)}\)
この両辺を比べれば
\(V_0 = \omega L I _0 \) ∴\(I_0 = \frac{V_0}{\omega L}\)
\(\phi = -\frac{\pi}{2}\)
(これは\(\cos{(x – \frac{\pi}{2})} = \cos{(\frac{\pi}{2} – x)} = \sin{x}\)です)
ということで、
\(I = \frac{V_0}{\omega L}\sin{(\omega t – \frac{\pi}{2})}\)
このように、式を推測する方法でも導けます。
電流と電圧の位相差は?
さてもうすこし電流に関してみていきます。
\(V = V_0sin{\omega t}\)
\(I = \frac{V_0}{\omega L}\sin{(\omega t – \frac{\pi}{2})}\)
注目すべきはsinの中身です
sinやcosの中身って位相を表わすという話はしましたね。
電流は電圧の\(\omega t\)に対して\(\frac{\pi}{2}\)だけ引かれているのがわかりますね。
これはつまり・・・
電流が電圧より\(\frac{\pi}{2}\)だけ遅れている
位相がずれているってことは、電圧が最大値を取っても電流は最大値を取らないってことです。
とまあ、正直それを知ってもあまりよくわからないと思うので、とりあえず電圧と電流にはそういう関係があるんだなあ程度に理解してもらえば大丈夫です。
ここまでが電流に関する話です。
実効値とリアクタンス

次は「交流を直流にみなす」ということを考えます。「交流を直流とみなす」とは言い換えれば実効値を使うという意味です。
実効値に関してはこちらの記事を参考にしてください。
実効値は電流と電圧の最大値が関係するので最大値を見ていきます。
電流の最大値\(I_0\)は先ほど式で導いています。
\(I_0 = \frac{V_0}{\omega L}\)
∴\(V_0 = \omega L I_0\)
実効値は「最大値の\(\frac{1}{\sqrt{2}}\)倍」だったので両辺\(\frac{1}{\sqrt{2}}\)倍すれば
\(V_e = \omega L I_e\)
となります。
あれ?なんかこれ、オームの法則みたい
 AI
AI
その通りですね。
\(R = \omega L\)と置けば
\(V_e = RI_e\)
見事にオームの法則になってます。
つまり、コイルは抵抗と同じ役割を果たしているんですね。
ということで、交流→直流としたときにコイルは抵抗と同じ役割を果たし、その抵抗の大きさが
\(R = \omega L\)となります。(これを誘導リアクタンスと言います)。
コイルは交流で一番大事
いかがでしたか?
コイルは交流回路でしか出てきません。直流だと何も起こりませんからね。
ですからコイルはしっかり理解を深めておきましょう。(もちろんコンデンサーも抵抗も大事です)
コイルのある回路について電流は電圧より位相が\(\frac{\pi}{2}\)遅れる
交流→直流に見立てたときのコイルは大きさ\(\omega L\)の抵抗になる。









