コイルの性質大公開!自己誘導やエネルギーを解説!

今回はコイルのお話です。
回路には抵抗、コンデンサ、コイルの3つをうまく扱うことが大事っス!
抵抗→\(V – RI\)
コンデンサ→\(Q = CV\)
コイル→??
と、まあ、こう見れば電圧と電流に関して何か関係がありそうですよね?ということで、今回はコイルの超基本的な性質について学んでいきます!
まずは性質を知らないと話にならないのでここはしっかり押さえてください!
コイルの性質→電磁誘導
コイルは導線からできています。では導線に電流が流れると何が発生しますか?
 AKINORI
AKINORI
はい!磁場です!
 AI
AI
では、コイルは円形の導線がいくつも並んだ構造をしています。なので、電流によってつくられた磁場がコイルの内部を通るとどうなりますか?
 AKINORI
AKINORI
・・・もしかして電磁誘導?
 AI
AI
はい。ここまで理解できたあなたなら、もうコイルの性質は理解できました!
コイルの性質の根本は電磁誘導です。電磁誘導が分かっているあなたならもういけますね。
・・・え?いけない??じゃあ、勉強しましょう!!
↓電磁誘導がやばいって人はこちらで↓
[blogcard url=”https://ryebourbon.xsrv.jp/electromagnetic-induction/”]
自己誘導
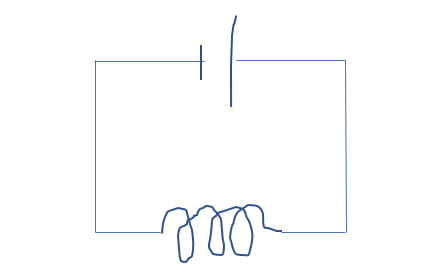
こういう回路を作ると面白いことが起こります。
この回路に電流計を置くと、いきなり針が振れるのではなく、だんだんと針が動いてやがて最大になるという現象が起こるんですよ。(実際には一瞬で針は振れます。あとこの回路はショートするので危険ですよ)
その理由はまさしく電磁誘導です。
誘導起電力が生じて、電池にによって流れる電流に逆らおうとするわけです。
ただ、受験生の皆さんはこれを式にしないといけないわけですね。というわけでやっていきましょう。
長さが\(L\)で断面積を\(S\)である\(N\)巻ソレノイドがある。このソレノイドに時間0から\(\Delta t\)の間に電流を0から\(\Delta I\)だけ変化させる。真空の透磁率を\(\mu\)として、この時の誘導起電力を考えてみましょう。
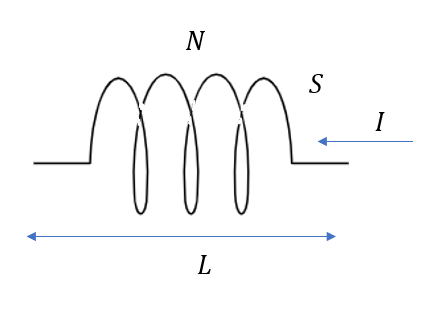
誘導起電力なので最終目標は
\(V = – N \frac{\Delta Phi}{\Delta t}\)ですね。
なのでまず磁束を考えましょう。
ソレノイドに生じる磁場は
\(H = nI = \frac{N}{l}I\) (\(n\)は単位長さ当たりの巻き数なので注意!!)
です。なので磁束密度は真空の透磁率\(\mu\)を用いて
\(B = \mu H = \frac{\mu N}{l}I\)
となる。よって磁束は
\(\Phi = BS = \frac{\mu N}{l}IS\)
右辺で変化するものは電流\(I\)だけなので、磁束の変化は電流の変化だけで決まります。
\(\Delta \Phi = \frac{\mu NS}{l}\Delta I\)
ここまで来たらファラデーの式を使えますね。電磁誘導の式はマイナスが付いてて厄介なのでまずは大きさから求めた方が良いです。
\(|V| = N\frac{\Delta \Phi}{\Delta t} = \frac{\mu N^2S}{l}\frac{\Delta I}{\Delta t}\)
\(\frac{\mu N^2 S}{l}\)は定数なのでこれをLと置けば
\(|V| = L\frac{\Delta I}{\Delta t}\)
これがコイルにかかる誘導起電力になりますね。
誘導起電力は磁束の変化を打ち消す方向。つまり右向きとなりますね。
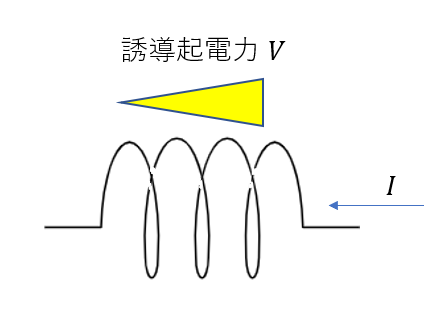
もう少し式を一般化していきます。
誘導起電力の正の向きは、磁束の時計回りと定めます。(一般的にそうです)
今回の場合、磁束は左向きに生じていますね。つまり、その右回りである左方向が起電力の正の向きなります。(基準点が右側なります)
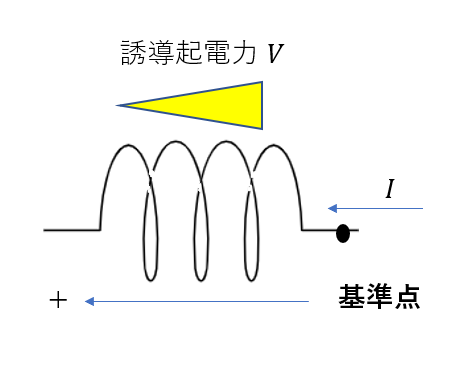
電流が増えた場合(\(\Delta I > 0\))、図のように起電力は右向きに生じます。(\(V < 0\))
つまり先ほど求めた大きさにマイナスをつければ良いんですね
\(V = – L \frac{\Delta I}{\Delta t}\)
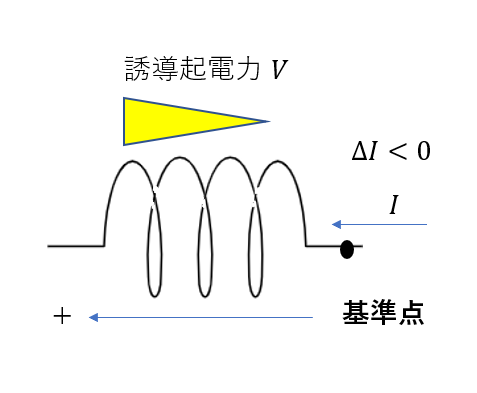
電流が減少する(\(\Delta I < 0\))の場合は、誘導起電力は左向きに生じます(\(V > 0\))
同じように、先ほどの式にマイナスをつけることで起電力を出せます
\(V = -L \frac{\Delta I}{\Delta t}\)
電流が増えようが減ろうが同じ式で表せましたね。
コイルの自己誘導起電力
\(V = -L \frac{\Delta I}{\Delta t}\)
*\(L\)は自己インダクタンス
うわ、ファラデーの電磁誘導の式とそっくり!!
 AI
AI
ファラデーの電磁誘導の式から導いたので似て当然ですね。
一般に式を出しましたが、基本は大きさを求めてから電圧マークをつけて向きを確認します。
相互誘導
先ほどのは自己誘導っていうもので、コイルが起電力を持つ場合の一つで、実はもう一つ相互誘導というのがあります。
これは入試ではほとんど問われないのでさらっと行きます。やっていることは自己誘導と変わらないです。
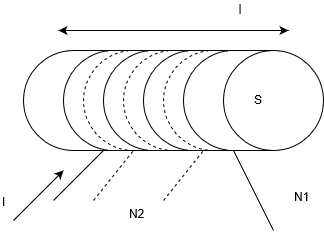
こんな感じで、巻き数がそれぞれ\(N_1, N_2\)巻のコイルを作ります。んで\(N_1\)巻の方に電流を流します。
自己誘導と全く同じように、\(N_1\)巻コイルが作る磁束密度は
\(B = \mu H = \mu・\frac{N_1}{l}I\)
なので
\(\Phi = BS = \frac{\mu N_1}{l}I・S\)
もちろん変化するのは電流だけなので
\(\Delta \Phi = \frac{\mu N_1 S}{l}\Delta I\)
このとき\(N_2\)巻コイルに生じる起電力について、大きさは
\(|V| = N_2\frac{\Delta \Phi}{\Delta t} = \frac{\mu N_1 N_2 S}{l}\frac{\Delta I}{\Delta t}\)
はい、\(\frac{\mu N_1 N_2 S}{l}\)は定数なのでこれを\(M\)と置けば
\(|V| =M\frac{\Delta I}{\Delta t}\)
うわ~。自己誘導にそっくり!!
ちなみに\(M\)は相互インダクタンスと言って、単位はヘンリー[H]。
向きついても自己誘導と全く同じなので、
\(V = -M\frac{\Delta I}{\Delta t}\)
が、これも問題では大きさ→向きっていう順序で解きましょう。
コイルのエネルギー
ここまでのコイルの特徴はつかめましたか?最後にコイルのエネルギーに関して説明して終わります。
コイルに起電力が生じるってことはエネルギーを蓄えているってことですよね。そのエネルギーの大きさを導いていきます。
自己インダクタンス\(L\)のコイルに、図のように微小時間\(\Delta t\)の間で電流を\(i\)から\(i + \Delta i\)まで増加させる場合を考えましょう。
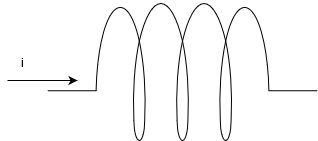
この時、誘導起電力の大きさは
\(V= L\frac{\Delta i }{\Delta t}\)
となりますね。図の向きの電流が増加するわけなので、起電力の向きは左向きですね。
さて、エネルギーと言えば仕事です。ここで、コイルの誘導起電力に逆らって電流を流すための電源の仕事を考えてみます。
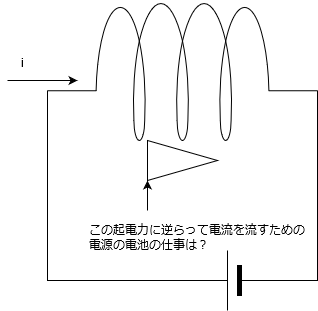
当然、誘導起電力\(V\)に逆らって電流を運ぶには\(V\)の起電力が必要ですね。また電流\(i\)は
\(i = \frac{\Delta q}{\Delta t}\)
と表すことができます(わからない人はこちら)
なので\(\Delta q = i\Delta t\)
電池がする仕事って何なのかというのをちょっとおさらいしておくと、電池って無理やり電圧を作り出して、電荷を運ぶ装置なんですよね。
電圧が生じるということは電場が生じるってこと。つまりその電場(静電気力)がする仕事が電池のする仕事ってわけです。それを求めようってやるんです。
電池の内部は一様な電場が生じています。
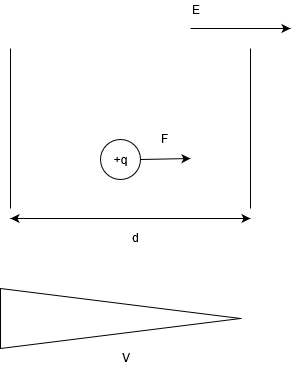
電荷\(+q\)が静電気力にされる仕事は
\(W = Fd = qEd\)
また一様な電場なので\(V = Ed\)、つまり
\(E = \frac{V}{d}\)
ということで
\(W = qV\)
となります。(電荷qを電圧Vで運ぶという感じですね)。
もちろん、これは起電力\(V\)が一定でなければいけません。電流が変化すれば起電力も変化するけど、微小変化を考えているから\(V\)は一定とみなしていいです。(これ、よく使う手法です)
なので、誘導起電力に逆らってした電池の仕事は
\(\Delta W = \Delta q V = i\Delta t・L\frac{\Delta i}{\Delta t} = Li\Delta i\)
となるわけです。
これは、グラフにすると・・・
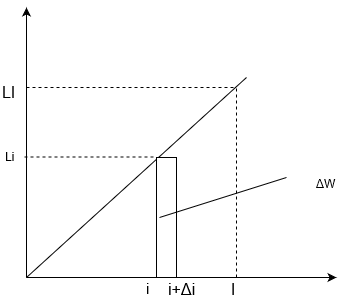
\(\Delta W\)は図の長方形の面積に当たります。
あとは電流\(I\)が流れるまでの仕事を求めるには、この長方形を0から\(I\)まで足していけばOKです。さらに\(\Delta i\)を0に近づけます。
すると三角形が出来あがりますね。この面積が最終的に持つコイルのエネルギーとなります。(つまり積分)
コイルのエネルギー
\(U = \frac{1}{2}LI^2\)
これで回路問題はすべて解けます
抵抗、コンデンサ、コイル。
この3つの性質を理解しておけば回路問題はもう解けます。なのでここで最後にまとめておきますね。
抵抗・コンデンサ・コイルの式まとめ
・電圧について
抵抗:\(V = RI\)
コンデンサ:\(Q = CV\)
コイル:\(V = -L \frac{\Delta I}{\Delta t}\)
・エネルギーについて
抵抗:\(W = IV\)
コンデンサ:\(U = \frac{1}{2}QV\)
コイル:\(U = \frac{1}{2}LI^2\)