白紙から説明せよ！電流の電子モデル化で定義I=vsneを導出！
今日はあれです。
久々の暗記です。
うわ～。Akinoriさんもそ～ゆ～ことしちゃうんですか
AI
そんな攻めないで（泣）。暗記っていうか、流れを完全に覚えてね！！っていうやつです。
AKINORI
あ。熱力学の気体分子運動論のところでやったようなやつですね！
AI
そうそう。白紙で説明できるようにしてほしいやつです。
AKINORI
ということで気体分子運動論に続き、白紙から説明講座の第二弾（というよりラスト）の
電流の電子モデル化です。
目標は
- 電流の式・・・\(I = vSne\)
- オームの法則
これを求めに行きます。
いってらっしゃい！
AI
いや、AIさん・・・あなたもやるんよ・・・
AKINORI
電流の定義
っとその前に電流の定義をしておきます
電流とは・・・
ある面を単位時間当たりに通過する電荷量
\(I = \frac{\Delta Q}{\Delta t}\)
＊向きは正電荷が動く向き
これが定義です。これをもとに、電流をもっと深く考えて、オームの法則まで導いてみましょう。
電流の電子モデル
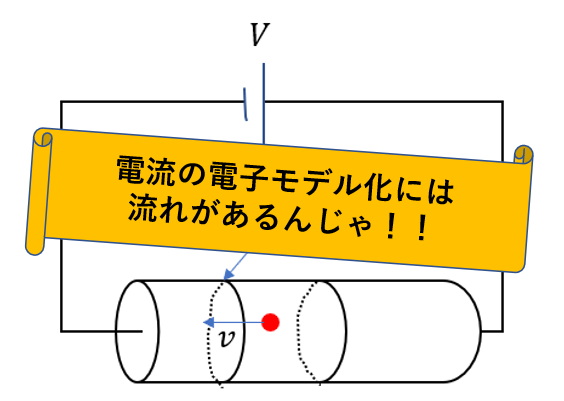
電子が平均の速さ\(v\)で面積が\(S\)の断面を通る。このときの電流について考えてみる。
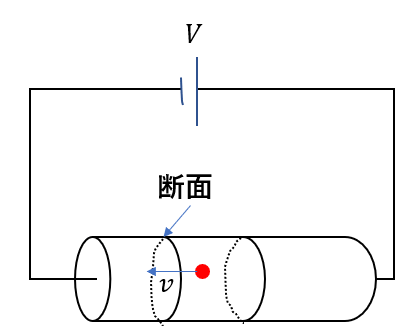
\(I = vSne\)「私はブスね」
電子が平均の速さ\(v\)で進みますね。
んで、電流は単位時間当たり、つまり１秒間あたりに通過する電荷量でした。
じゃあ、一秒間に通過できるような電子はどこにあるものでしょう？
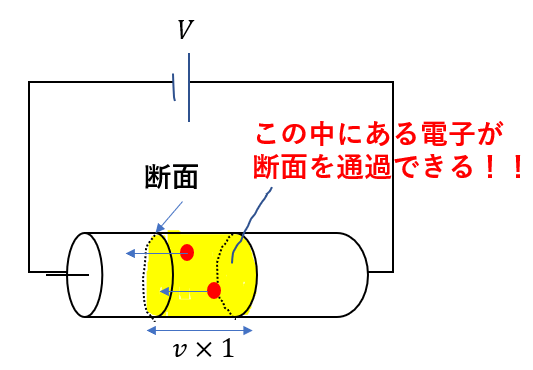
１秒で\(v\)進むんですから、図の色がついている空間にある電子が断面を通過できますね。
なので、この中にある電子の個数さえ分かればいいんですね。
電子の単位体積当たりの個数、つまり密度を\(n\)とすれば
通過する電子の個数\(N\)は\(n \)に体積を掛ければいいですよね。
\(N = n \cdot (v\times S)\)
電子一個の電荷量の大きさは\(e\)（電気素量）なので、電流の大きさは
\(I = e\cdot N = vSne\)
と表すことができますね。
まずこれが一つ。
うわ～こんなの覚えられないよ！
AI
\(I = vSne\)を続けて読むと、「私（I）はブスね」。こうやって覚えちゃって！
AKINORI
私そんな、自分でブスなんて言えない！！ムリムリ。
AI
・・・・・次行くよ！
AKINORI
オームの法則を導く
上の抵抗を考えてみましょう。
抵抗には電位差が生じているんですから、もちろん電場が生じていますね。
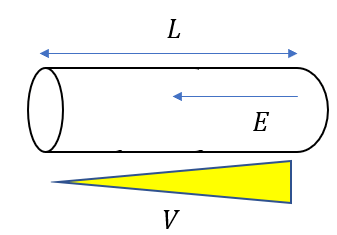
この電場は一様です。
なので
\(V = EL\)
∴\(E = \frac{V}{L}\)
となりますね。
すると、電子はこの電場によって静電気力を受けます。
１[C]の電荷が受ける静電気力の大きさが\(E\)なので
e[C]の電荷が受ける静電気力の大きさは\(eE\)です。
よって電子が受ける静電気力は
\(F_1 = e\frac{V}{L}\)
ですね。
あれ？でもそしたらおかしくありません？平均の速さを考えているから速さは一定ですよね？でも力を受けたら加速度が・・・
AI
そうだね。でも、抵抗内には陽イオンが存在しているよね。それから受ける力があるはず。それとつり合うはずだ。
AKINORI
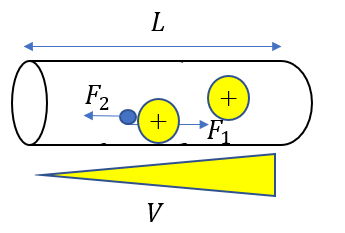
抵抗内には陽イオンがあって、それとぶつかりながら電子は進んでいきます。
陽イオンの数は無数なので、連続的に、常に力を受けていると考えれば、この抵抗力と静電気力がつり合って速さが一定に保たれますね。
抵抗力は、空気抵抗の場合と同じで
\(F_2 = kv\)
として、
\(F_1 = F_2\)
∴\(v = \frac{eV}{kL}\)
これをさっきの
\(I = vSne\)
に代入すれば
\(I = \frac{eV}{kL} \cdot Sne\)
\(V = \frac{k}{e^2 n} \frac{L}{S} \times I\)
はい、
\(R = \frac{k}{e^2 n} \frac{L}{S}\)
（定数）と置けば
\(V = RI\)
でました～。オームの法則ですね！
AI
ということでオームの法則が出ました。
また、抵抗について見てみると
\(\frac{k}{e^2 n}\)というのは抵抗の材質に依るので、これを新たに\(\rho\)（抵抗率）として整理すると
\(R = \rho \frac{L}{S}\)
これを見れば
- 抵抗が長いほど
- 断面積が小さいほど
抵抗が大きい、つまり電流が流れにくくなる
ということです。
電流を電子レベルで考えるとオームの法則が導けるんですね！！
AI
抵抗によるジュール熱
最後に、抵抗に関連して抵抗の消費電力というのを考えてみます。
電力はつまるところ、「仕事」です。
１個の電子が\(t\)秒間で電場（静電気力）からされる仕事は、
さっきの\(F_1\)は一定なので「力×距離」と書けます。
そして\(vt\)だけ進むので
\(w = F_1\cdot vt = \frac{eV}{L} \cdot vt\)
抵抗中には\(n \cdot SL\)個の電子があります。なので、電子全部がされる仕事は
\(W = w\cdot nSL = vSne\cdot Vt\)
はい、\(I = vSne\)「私はブスね」です。これを使うと
\(W = IVt\)
全電子の流れっていうのは、電流のことですよね。
なのでこの\(W\)は
電流のした仕事
となります。
抵抗では電流が流れると熱が出ます。
スマホを使っていると熱くなってきますが、それも電流が流れたときに抵抗が熱を出しているからです。
これは、電子が電場によって仕事されてエネルギーを持つんだけど、陽イオンにぶつかって結局失っちゃう。
その失った分が熱として放出されるんですね。
といわけで、この熱をジュール熱と呼んで
\(Q = IVt\)
と書けます。
そして、消費電力はこの仕事率と定義されていますので、
\(P = \frac{W}{t} = IV\)
となります！
以上で終わりです！
AKINORI
はい。白紙から記述できるように理解しておきます！！
AI
