微積よりもベクトルを学べ！高校物理で符号ミスしてしまう理由は・・・
このサイトではベクトルっていうのをよく使っているけど、本当に意味あるんですか？
AI
どうして？
AKINORI
私が見てきた参考書には全くベクトルの話なんて書いてないし、使わなくても解けることが多いから疑問に思っちゃって・・・
AI
確かに、あまり参考書では取り上げてないかもしれないね。でも、ベクトルを知らないと符号ミスにつながっちゃうんだ。
AKINORI
多くの参考書にはベクトルは取り上げられてない
このサイトでは、ほとんどの参考書では取り上げていない、「ベクトル」の解法を教えています。
たぶん、多くの人がベクトルを意識していないかもしれませんね。
でも、これは実はめちゃめちゃ大事なものなんですよ。
物理で出てくる量（物理量）の多くは「向き」と「大きさ」を持っています。
例えば、速度、加速度、力です。
速度でいえば、単に「10m/s」と言っても「東向き」か「西向き」かで全然違いますよね。
物理は基本「向き」と「大きさ」両方を考えて初めて意味を持つものなんです。
そして、数学で「向き」と「大きさ」を持つものと言えば・・・
そう、「ベクトル」です。
だから、僕は「ベクトル」を意識するようにしているんです。
でもね、多くの参考書では取り上げていないのはなぜでしょう？
高校物理はかなり数学的な話を避けようとする傾向があります。
微分積分を使わないということからわかりますよね。
ですから「ベクトル」というのもあまり使いたくないので、参考書では取り上げていないのです。
ただ、これが後で混乱を呼ぶことになるかもしれません！
物理で怖いのが「符号ミス」
なるほど。でも、やっぱりベクトルを意識していなくても解けているから大丈夫かと・・・だから参考書では取り上げていないんじゃないんですか？
AI
いや、ベクトルを意識しないと全部破綻する問題も少なくないんだ。その理由が「符号ミス」にあるんだよ
AKINORI
そう、ベクトルを意識していないと、特に難関大に行ったときに地獄をみるかもしれません。
その地獄を見る最悪のミスが「符号ミス」です。
例えばこんなことを考えてみましょう。
図のように質量\(M\)の台の上に質量\(m\)の物体を置く。はじめ、台と物体は静止しているとする。ある時刻での物体の速度を\(v\)、台の速度を\(V\)とするとき、\(v , V\)の関係を式に表せ。ただし、すべての面で摩擦は無視し、台と物体には内力のみが働いているとする。
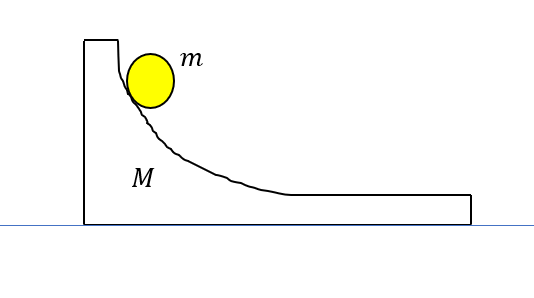
(2016 セミナー物理基礎＋物理 問188 改）
さて、この問題はいたって単純。
「運動量保存則を使う」だけ！
え～！こんなの簡単じゃん。物体は右向きに動いて、台は左向きに動くんだから。右向きを正にして考えれば
\(mv – MV = 0\)
ですね！
AI
あ、やっぱり間違えたね。これはベクトルを意識していないと間違えちゃう問題なんだ。
AKINORI
あなたも同じように間違えたのでは？
この間違いは「ベクトルを意識していない」ことに原因があるんです！
AIさんが考えたことをもう一度確認してみましょう。
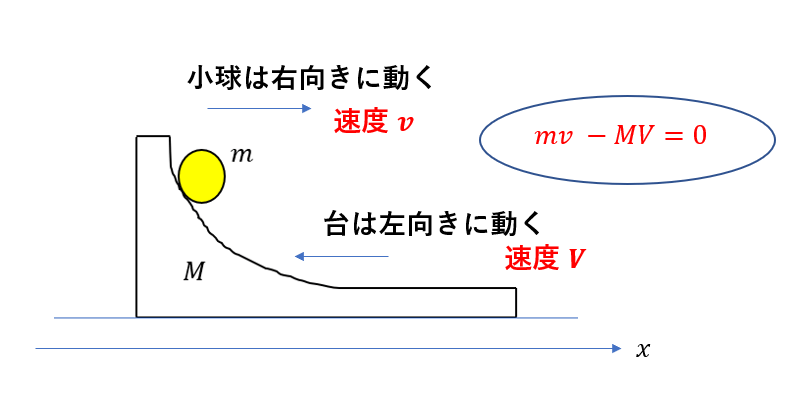
今回、水平方向で考えれば運動量保存が成り立ちます。
はじめ、両者は静止しているので運動量は０。
そして、物体は速度\(v\)で、台は速度\(V\)で動いているとすると、見るからに、物体は右向きに動いて、台は左向きに動くのはイメージできるよね。
だから、例えば右向きに正を取れば、台は逆向きなのでマイナスだ！
ってことで、運動量保存を考えると
\(mv – MV = 0\)
というのがAIさんの考えかたです。
うん。そういう考え方をするのはよくわかる。でもね、肝心なことを忘れているんだよ。もう一度問題文を読んでみよう。
AKINORI
問題文にはこう書いてあります。
物体の速度を\(v\)、台の速度を\(V\)
今回使っている\(v , V\)っていうのは「ベクトル」なんです。
だって、速度っていってるんだもの。
矢印記号がないから混乱するかもしれないけど、
要はこの\(v , V\)は\(\vec{v} , \vec{V}\)とおんなじ意味を持っている。
もっと言えば、\(v = (〇) , V = (△)\)
という表記ができるってわけだ。
そして、運動量はそもそも定義がこうでした。
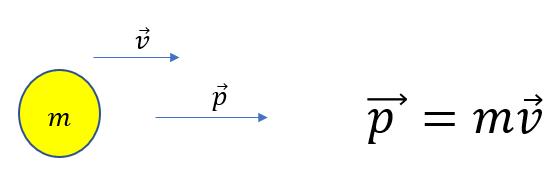
速度\(\vec{v}\)、質量mのとき、運動量の\(\vec{p}\)は
\(\vec{p} = m\vec{v}\)
つまり、速度というベクトルを用いたものですね。
だから、さっきの問題でいえば右向きに動こうが、左向きに動こうが、
問題文で速度をそれぞれ\(v , V\)と与えられているので、運動量の和は
\(mv + MV\)
となるわけなんです。
つまり、答えは
\(mv + MV = 0\)
です。
でも、物体が右向き、台が左向きに動くのは確かですよね？逆向きを表すマイナスはどこに行ったんですか？
AI
良い質問だね。それはベクトルを成分表示したときに現れるんだ。
AKINORI
ベクトルの式は必ず成分を代入して計算するのでした。
仮にこの問題の速度を
\(v = (v_1)\)
\(V = (-V_1)\)
と成分表示できたとすれば。さっきのベクトルの式に成分を代入して
\(mv_1 – MV_1 = 0\)
となる。
ここで、初めてマイナスというのが現れてくるんです！
なるほど。ちゃんとベクトルを意識していないとだめなんですね。
AI
そうなんだ。この問題は実は入試問題の最初の問題なんだ。そしてこの結果を使って次の問題を解いていくから、ここで間違えちゃうと残りの問題も間違えちゃう。怖いよね。
AKINORI
混乱のポイントは問題文でベクトルを\(\vec{v}\)みたいに矢印で表していないことにあります。
多くの問題では\(\vec{v}\)のような表記はあまりなくて、単に\(v\)と表すのがほとんどなんです。でも速度とか加速度みたいにベクトルを表す言葉に注目して、ベクトルとしてこの文字を扱っていかないといけません。
（初見殺しです（笑））
結局僕が言いたいのは
ということで、ベクトルの重要性が分かったでしょうか？
しっかり復習してくださいね。
無料プレゼントで勉強しません？
ただ、ほとんどの参考書ではここまで注意深くやっていないわけです。
だから勉強もしにくい！
なので、僕が作った無料プレゼントをもらって勉強してください！！
もちろん無料で！
今すぐ読もう！！
↓無料プレゼント↓
それでは！！
Comment
問題に不備があるように思います。速度vと速度Vの正の向きを問題の中で指定する必要があります。どちらも右向きを正とすれば、記事の中でおっしゃる通りですが、正の向きを互いに反対(vは右向き正、Vは左向き正など) にとっておけば、mv−MVが正しくなります。