【高校物理】慣性力の意味を完全理解!公式ではなく運動方程式から学ぶ

・慣性力の本当の正体が分かる
・慣性力の大きさががなぜ\(ma\)なのかが分かる
・慣性力の向きがなぜ観測者と逆向きなのか分かる
・慣性力の問題での使い方が分かる
どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
あっきーさん。慣性力って何ですか?「加速度と逆向きで\(ma\)の大きさの力」?・・・全然意味わからないんですけど
 リケジョ志望のAIさん
リケジョ志望のAIさん
円運動あたりで突如現れるこの単語。
慣性力
いきなり慣性力なんて言葉が出てきたにも関わらず説明は・・・
加速度\(\vec{a’}\)で運動している観測者から見たとき慣性力\(-m\vec{a’}\)が働いているとして運動方程式を立てると
\(m\vec{a} = \vec{F} – m\vec{a’}\)
のような意味が分からない説明をされて悩んでいませんか?
実はこの慣性力は難しくなく、ごく当たり前のことなのです。
なぜなら、慣性力というのは「相対速度」と考え方が同じなのです。そして運動方程式を使った結果、後付けされたものにすぎないからです。
この記事では、教科書の説明から離れて、相対速度や相対加速度の観点から慣性力がなぜ生まれたかを説明してきます。
最後まで読むことで、慣性力というイメージしにくいものが明確になり、公式いらずで知ることができます。
目次
慣性力は相対加速度から生まれる

慣性力というのは結論から言いますと、自分が動きながら物体を見るときに働く力のことです。
それを運動方程式を立てることで理解することができます。
運動方程式というのは実は前提条件として「自分が加速度運動していない場合(慣性系)」にのみ適用できる公式なのです。
え?そうだったんですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
意外と知らない人が多いので、これは覚えておきましょう。
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
ですが、自分が加速度運動をしている場合にも同じように運動方程式を適用したい。
そう思ったときに考え出されたのが慣性力なんですね。
そのような背景を頭に入れたうえで詳しく見ていきましょう。
相対加速度って何?→相対速度と同じ考え方

まず相対加速度に関してお話をしておきたいと思います。これが今回カギになります。
先ほど言ったように運動方程式は「自分が加速度運動してない場合」に成立する公式でした。大雑把に言えば「自分が止まっている」場合に成立するものです。
そして、相対速度の記事ではこんな話をしました。
相対系、つまり「〇〇から見ると・・・」ということは、結局
「止まって見る」ことと同じだった!!
こういうことでしたね。
つまり「動いて見る」→「止まって見る」に置き換えることで運動方程式を使えるようにするというわけです。この操作を行うために「相対加速度」という概念が必要になってくるというわけです。
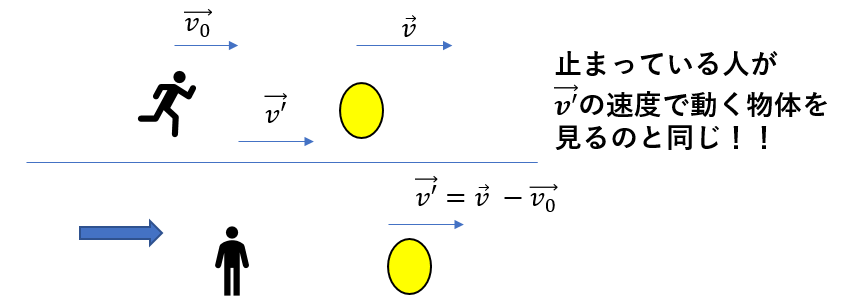
動きながら物体を見る場合、自分が止まって見る分、相手に自分の速度だけ補正してあげればよかったんですね。
止まって見たら\(\vec{v}\)の速度に見える物体を
自分が\(\vec{v_0}\)の速度で動いている状態で見ると、見え方は変わります。
その見え方は\(\vec{v’} = \vec{v} – \vec{v_0}\)です。
これは、あたかも
自分は止まっていて、物体が\(\vec{v’} \)の速度で動いている。
とみなすことができるのです。
「自分は動いているんだけど『止まって見る』に置き換える代わりに、自分の速度\(\vec{v_0}\)を引いて補正したんだよ」
ということです。
このことは加速度についても同じように言えます

止まって見たら\(\vec{a}\)の加速度に見える物体を
自分が\(\vec{a_0}\)の加速度で動いている状態で見ると、見え方は変わります。
その見え方は\(\vec{a’} = \vec{a} – \vec{a_0}\)です。
これは、あたかも
自分は止まっていて、物体が\(\vec{a’} \)の加速度で動いている。
とみなすことができるのです。
「自分は動いているんだけど『止まって見る』に置き換える代わりに、自分の加速度\(\vec{a_0}\)を引いて補正したんだよ」
っていうことです。
これが相対加速度のお話です。簡単ですね。
速度で成り立つことは、加速度でも成り立つのはなんとなく分かると思います。
相対速度や「相対系」というものに関してはこちらをご覧ください。
慣性力を運動方程式から導こう
ではいよいよ本題です。この設定で運動方程式を立てていきましょう。
加速度\(\vec{a_0}\)で運動している観測者から見たとき物体の加速度は\(\vec{a’}\)であった。床に対する物体の加速度を\(\vec{a}\)、物体に働く合力を\(\vec{F}\)としたとき、この物体の運動方程式を立てよ。

こんなの簡単じゃん!!加速度は\(\vec{a’}\)だから、運動方程式は
\(m\vec{a’} = \vec{F}\)ですね。
 リケジョ志望のAIさん
リケジョ志望のAIさん
とやってしまうとアウトです。
何度も繰り返しますが、運動方程式は「自分が加速度運動していないとき」に成立する公式です。
この問いでは\(\vec{a’}\)というのは加速度運動している観測者から見たときの物体の加速度です。つまり、運動方程式に適用できないんですよ。
今回は「床に対する加速度\(vec{a}\)」を使わなければなりません。「床に対する」というのは「止まっている観測者から見た」という意味なので、運動方程式の条件に合いますね。
ということで、運動方程式は
\(m\vec{a} = \vec{F}\)
となります。
ここからもう少し詳しく見ていきます。
今回の問いでは止まっている観測者から見た加速度は\(\vec{a}\)と与えられていますが、実際のところこれが分かるならわざわざ動きながら観測する必要はありませんよね。
止まって見たときの加速度が分からなくても、動きながら見たときの物体の相対加速度が分かっている場合に、この相対加速度を使ってダイレクトに運動方程式を作れた方が楽だと思いませんか?
ということで、今回は相対加速度\(\vec{a’}\)を含む式に変形したいと思います。
先ほどの通り
\(\vec{a’} = \vec{a} – \vec{a_0}\)
ですから
\(\vec{a} = \vec{a_0} + \vec{a’}\)
です。これを代入してみましょう。
\(m\vec{a_0} + \vec{a’} = \vec{F}\)
\(m\vec{a’} = \vec{F} – m\vec{a_0}\)
この式に注目!!

右辺の\(m\vec{a_0}\)を見てください。
これ、「質量×加速度」の形になっていますよね。
つまり、運動方程式の形になっているんですよ。
運動方程式ってのは
「質量×加速度=合力」
ですから、\(m\vec{a_0}\)ってのは何らかの力を表さないといけないわけです。
この何らかの力っていうのが
「慣性力」
です。
(正確には\(-m\vec{a_0}\)というように、マイナスも含めて慣性力です)
え?これだけですか?なんか簡単に出ましたね
 リケジョ志望のAIさん
リケジョ志望のAIさん
このように、慣性力というのは普通に運動方程式を立てることで導かれるものなんです。
次は、この慣性力の意味について考えてみましょう。
慣性力の意味

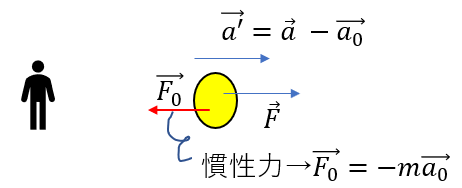
もう一度、慣性力を式で確認してみましょう。
\(\vec{F_0} = -m\vec{a_0}\)
*マイナスも含めて慣性力です。
\(\vec{a_0}\)というのは、「観測者の加速度」でした。
そして、マイナスというのは「逆向き」という意味。
つまり・・・
「自分の加速度の向きと逆向きに力が生じている(ように見える)」
これが慣性力の特徴です。
これをもう少し考えてみましょう。
そもそも、観測者に加速度が生じているのは
観測者に力がかかっているからです。
運動方程式\(m\vec{a} = \vec{F}\)を見れば、力\(\vec{F}\)がかかることで加速度\(\vec{a}\)が生じることが分かりますね。
観測者について運動方程式を立ててみるとこうなります。
\(m_0 \vec{a_0} = \vec{F_0′}\)(\(m_0\)は観測者の質量)
あれ?これってさっきの慣性力に似てませんか!?
 リケジョ志望のAIさん
リケジョ志望のAIさん
そうだね。これにマイナスをつけて、\(m_0\)を\(m\)に置き換えたらまさに慣性力ですね。
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
この\(\vec{F_0′} = m_0 \vec{a_0}\)
という式に
・マイナスをつける
・\(m_0\)を\(m\)に置き換える
→慣性力\(\vec{F_0} = -m\vec{a_0}\)になる
というこの部分は実は非常に重要な意味を持っています。
マイナスというのは「補正する」という意味があります。
\(m_0\)を\(m\)に置き換えるというのは、「観測者の質量」を「物体の質量」に置き換えるということです。つまり、自分に関する力を、物体に置き換えるということになるわけです。
お分かりですか?慣性力というのは・・・
「自分にかかる力を相手に逆向きに押し付けたもの」
というわけです。
あれ?この話は相対速度(相対系)の話で見たことある。確か・・
 リケジョ志望のAIさん
リケジョ志望のAIさん
まさにその記事で説明した通り、
「動いて見る」を「止まって見る」に言い換えるために補正したのです!!
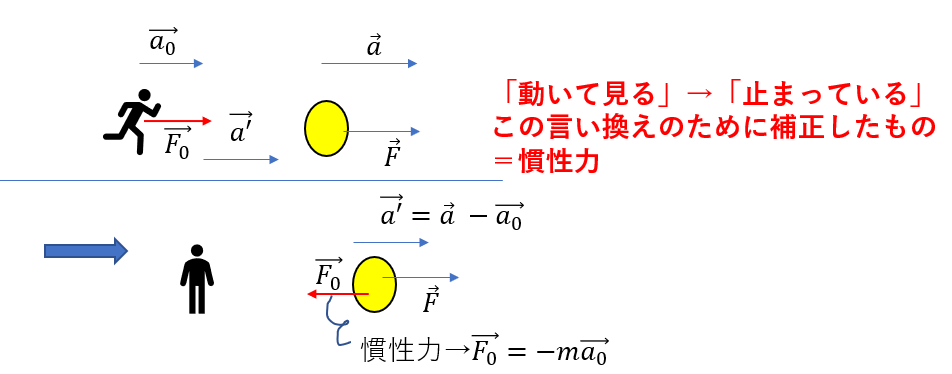
これが慣性力の真の意味です。理解できましたか?
慣性力は補正のための力なので、実際に働いているわけではないです。
仮想の力です。
運動方程式について、
「動いて見る」→「止まって見る」の言い換えを
表した式がまさに、この式です。
\(m\vec{a’} = \vec{F} + \vec{F_0}\)
(\(\vec{a’} \)は相対加速度。\(\vec{F_0} = -m\vec{a_0}\)は慣性力)
左辺は相対加速度を使っています。最初の方に説明した通り、相対加速度は「動いているのを止まって見るものに置き換えますよ」というものです。
そして、止まって置き換える代わりに、右辺で自分に働いていた力を物体に押し付けて補正しますよ。
ということなのです!!
なるほど。慣性力はただ補正するために便宜上使った力ってわけですね
 リケジョ志望のAIさん
リケジョ志望のAIさん
そう!よく理解できてるね。
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
「相対系は『動いて見る』→『止まって見る』の言い換え」
ということと
「言い換えるときには何かを補正する必要がある」
ということ。
ここから、慣性力を導いたことに過ぎないんですね。公式なんてないということが分かってでしょうか?
遠心力も慣性力

高校ではこの慣性力の一種として遠心力が紹介されています。
「遠心力」と名前がついていますが、結局のところは慣性力です。
なので、今回の理解があれば遠心力についても簡単に理解ができます。
遠心力について詳しくはこちらを見てください。
問題で慣性力の使い方は?

慣性力に関しては理解できました。でも、問題ではどのように使うんですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
実際に問題を解いてみよう!
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
慣性力の問題
質量\(m\)の物体が図のような台に乗っている。この台を大きさ\(a>0\)の加速度で等加速度運動させる。この物体が台に接しながら滑るための加速度の大きさ\(a\)を求めよ。
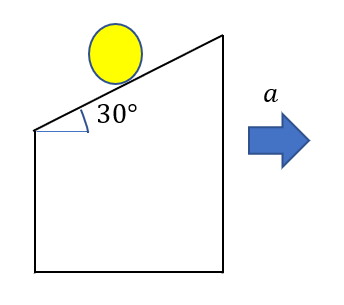
慣性力を使う→力のつり合いにもっていく
慣性力は力のつり合いにもっていくために使います。
もし止まったまま物体を見ると少々面倒なことが起こります。
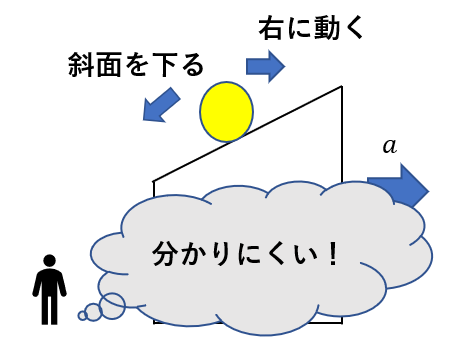
物体は台に乗っているから右向きに動きますね。
一方斜面を下る動きも同時に起こります。
・・・混乱しません?
そこで、「右方向に動く」という部分をキャンセルします。
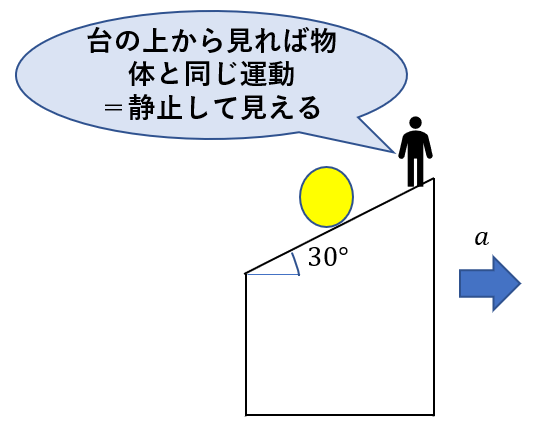
このように、台に乗って考えれば物体の右方向の動きはキャンセルされます。ですから、この人から見た場合、ただの斜面を下る運動に見えるのです。
慣性力→力のつりあいに持っていける
後は力を書いて条件を当てはめていくだけですが、台に乗って考えているので慣性力が働きます。
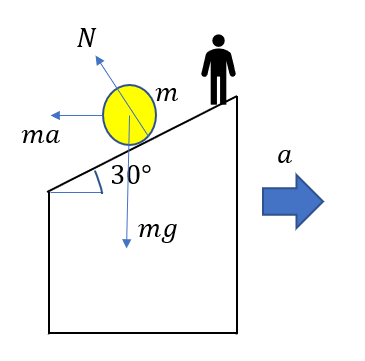
斜面を下る運動なので、当然斜面に沿って水平・垂直方向で考えますね。
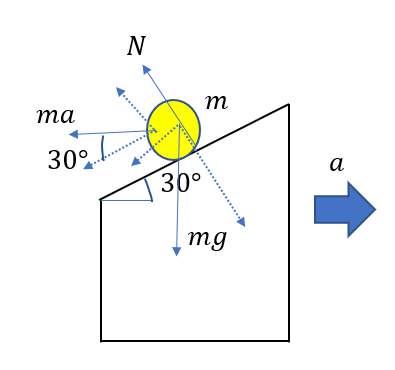
何度もしつこいですが、斜面を下る運動なので、このように力を分解した場合、斜面垂直方向の力はつり合いますね。
なので次のように関係式が得られます。
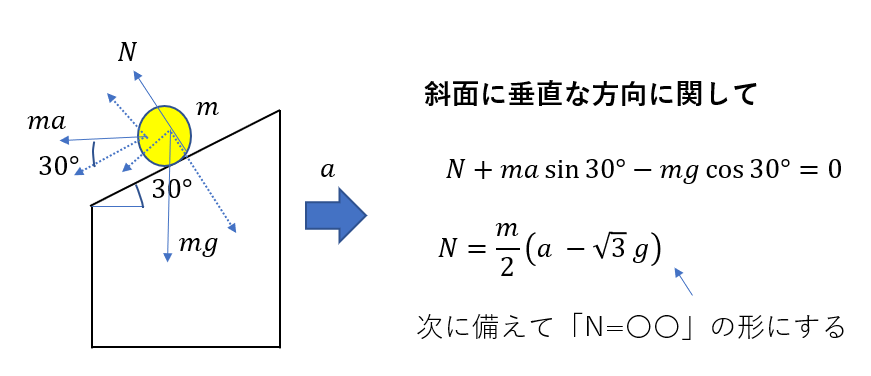
今回の問題では「斜面に接して・・・」とあるので垂直抗力が働いていなければいけないということです。
つまり\(N \ge 0\)としてまとめると
\(0 < a \le \sqrt{3}g\)
これが答えになります。
慣性力は複雑そうな運動に使える
最初は「右に動くの?滑り下りるの?」と混乱しますが、慣性力を使うことによって「斜面を下る単純な運動」になり、そこから力のつりあいにもっていくことができました。
一見複雑そうな運動でも物体と同じように動くことで単純化できるのです。
これが慣性力のメリットです。
この複雑そうな運動を単純化するのは「相対速度」や「二体問題」でも使われている手法で、やり方は慣性力の場合と同じです。何かに乗って考えるんです。
これらの例は以下の記事で詳しく説明しますね。
まとめ:慣性力はただの「補正」

いかがでしたか?
慣性力がいきなり出てきて「ん?ナニコレ?」と思った方は理解が深まったんじゃないでしょうか?
学校や教科書では、「相対系」というものを説明せずいきなり慣性力について説明するから公式のように覚えさせられるわけです。
「相対系」という「動いて見る→止まって見るの置き換え」の概念があって、その中に相対速度だったり慣性力があるわけですね。相対系の理解なしに慣性力の意味は理解できないわけです。
慣性力の使い方に関してはこちらで確認しましょう!!
- 相対系の意味
・「動いて見る」→「止まって見る」の言い換え
・言い換えのために何かを補正する必要がある
相対系の意味を踏まえて運動方程式を立てる「慣性力」が出てくる
→「自分に働く力を、相手に押し付けて補正する」
慣性力:\(\vec{F_0} = -m\vec{a_0}\)
(\(m\):物体の質量、 \(\vec{a_0}\):観測者の加速度)
オンライン物理塾長あっきーからのお知らせ!
勉強を頑張る高校生向けに2週間で力学をマスターし、偏差値を10上げるオンライン塾を開講してます!今ならすごいサポート特典もあります!
*無料の物理攻略合宿よりも充実のコンテンツです!









Comment
4.慣性の意味 までは観測者が「動いている」から「止まっている」という方向で話が進んできたが、5.遠心力も慣性力 以降は観測者が「止まっている」から「(物体と一緒に)動いている」というこれまでとは反対方向に話が進んでいるように思える。 観測者の立場の変換が4までと5以降で逆となっていて理解しにくいと思います。
いつも参考にさせていただいています。まもなく2次試験の時期ですが、最近もお世話になってます。
慣性力の問題の部分で、斜面に垂直な成分に関するつり合いの式の結論であるN=〜の式で、m/2×(√3g-a)ではなくm/2×(a-√3g)となっているのは何故なのか上手く理解できません。
お忙しいこととは思いますが、何卒解答よろしくお願いします。
コメントありがとうございます。
僕の表記ミスですね。ご指摘ありがとうございます!
大変な時期ですが、試験頑張りましょう!
自分に働く力を相手に逆向きに押しかけることで、相対加速度を用いて運動方程式を立てることが出来る。止まって見ている状態と等しくなる。
いいですね!その通りです。
高校2年生ですよね?理解力すごいです!