誰も知らない見かけの重力の使い方とは?慣性力の振り子問題解説

どうも!オンライン物理塾長あっきーです。現役で早稲田大学に合格し、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
見かけの重力というのが出てきたのですが、これってどういう意味なんでしょうか?問題で使えるのかいまいちわかりません!
 リケジョになりたいAIさん
リケジョになりたいAIさん
今回はこの悩みを解決します。
結論から言いますと見かけの重力の意味と使い方は以下の通りです。
見かけの重力:重力と慣性力の合力
→見かけの重力を使うと地面で静止した人から見る運動に置き換わる
この性質を使うことで名門の森レベルの問題はもちろん、入試問題も簡単に解くことができます。
見かけの重力について詳しく見ていきましょう!!
目次
見かけの重力とは慣性力と重力の合力
教科書や問題集の解説でいきなり「見かけの重力」という言葉を目にしたことがあるかと思いますが、一般に以下のように説明されています。
見かけの重力:慣性力と重力の合力
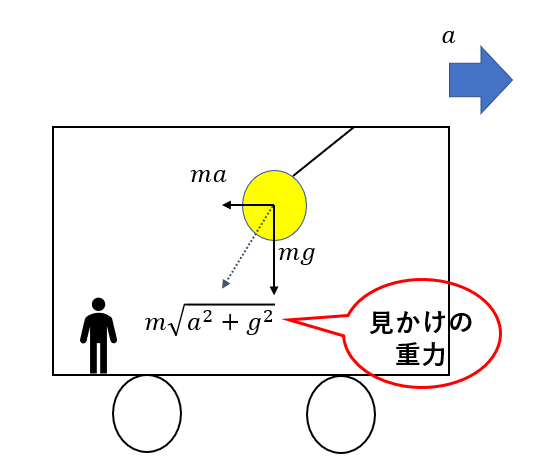
例えば図のように、右向きに大きさ\(a\)で加速度が生じている電車の中で糸につるされている物体を見ると慣性力が大きさ\(ma\)で働いています。
慣性力と重力の合力が見かけの重力となるわけです。
重力と見かけの重力のなす角を\(\theta\)とすれば
\(\tan{\theta} = \frac{a}{g}\)
が成立します。

電車に乗った人から見た場合、物体は静止して見えるので見かけの重力と糸の張力がつり合いますね。
ここの説明で慣性力の話が出てきました。慣性力についてはこちらの記事をチェックしましょう!
誰も知らない見かけの重力の真の意味
ここまでは教科書に載っていることの内容です。しかし重要なのはここじゃないです。
見かけの重力はある重要な役割を持っています。
それは置き換えです
電車の中と外で見る場合を比較する
置き換えをするには2つの状況が同じようになる必要があります。
そこで、止まっている電車(加速度運動していない)の外から見た場合と、加速度運動している電車の中から見た場合を比較します。
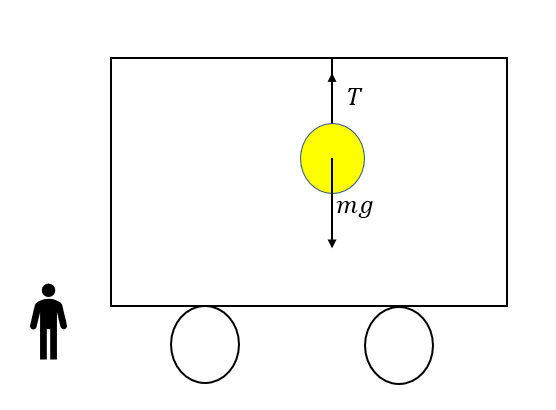
電車は加速度運動しおらず、物体は鉛直方向に吊り下げられた状態です。
この場合は、図のように鉛直方向で張力と重力がつり合います。
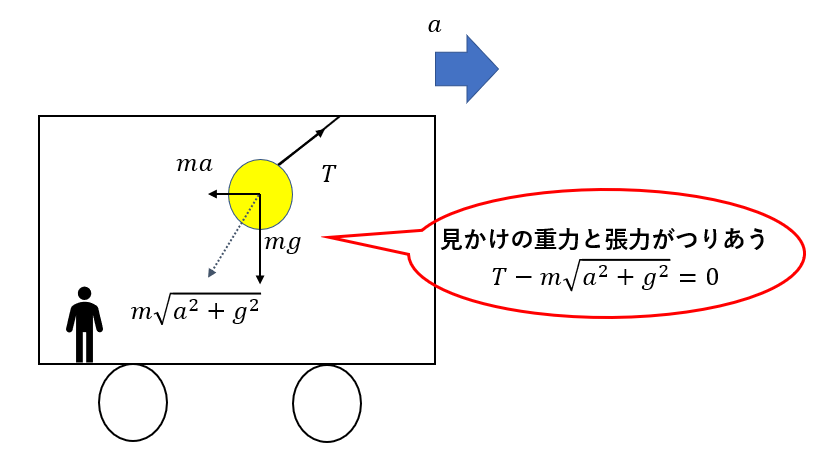
電車に乗って見ると、先ほど見たように斜め方向で見かけの重力と張力がつりあいます。
見かけの重力を使うと軸を変えることができる
この2つ比較すると面白いことに気づきます。
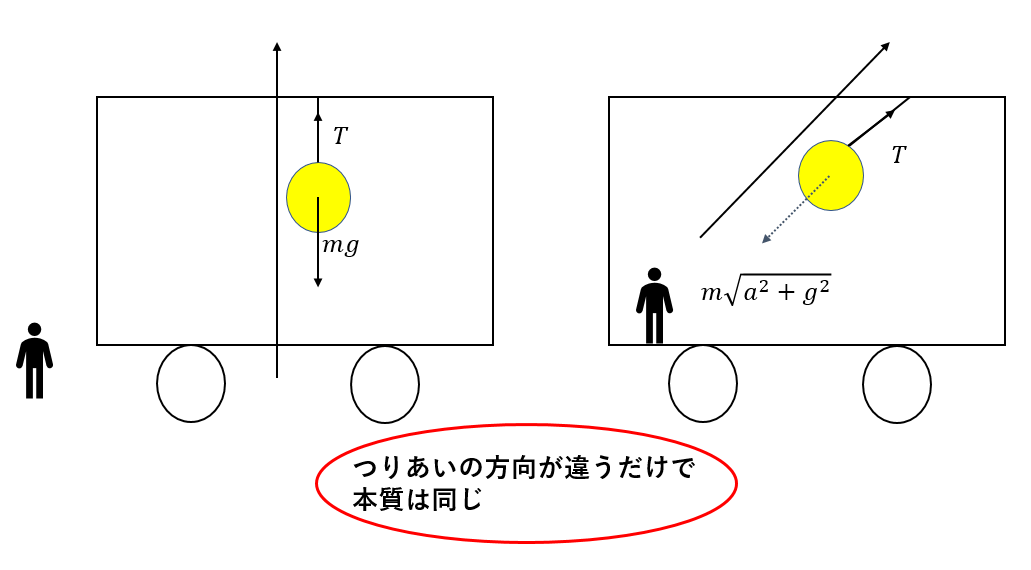
つり合いの方向は違うにせよ、「重力と張力のつりあい」ということに変わりはありません。
つまり、軸を回転させてしまえばどちらも同じ状況が作れてしまうのです。
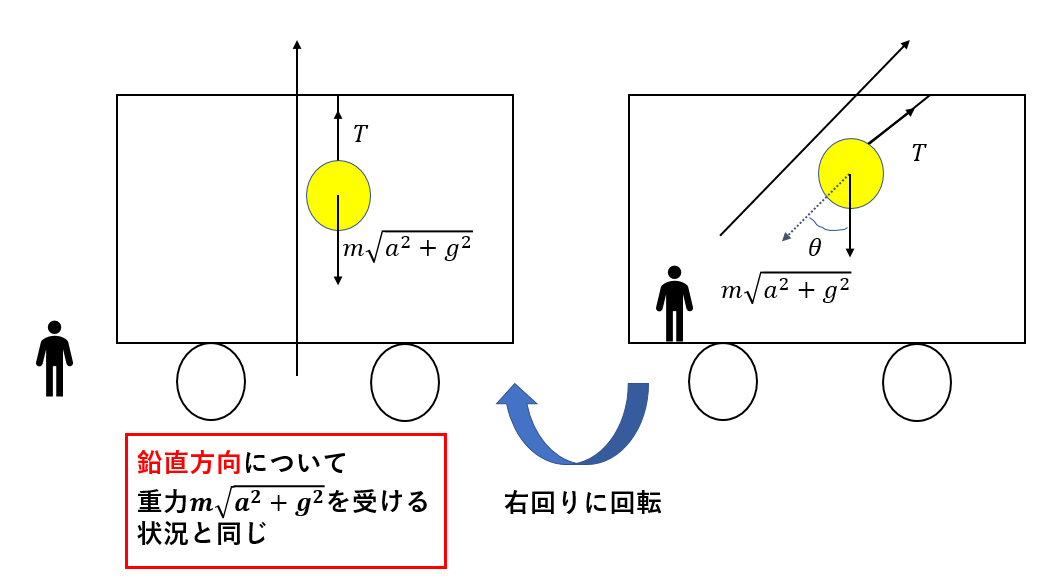
見かけの重力を使うことで、鉛直方向に吊り上げられた物体にみなすことができるのです。
ただ、重力の大きさは\(m\sqrt{a^2 + g^2}\)となります。
見かけの重力の考え方は慣性力と同じ
これはまさに「慣性力の置き換え」と同じです。
自分が加速度運動しているのを止まった状態に置き換える。その補正として重力加速度を\(g \to g’\)にする
見かけの重力は慣性力から来ているので、考え方も同じなのです。
このことが分かっていると、見かけの重力の使い方が見えてきますね。
以降で見かけの重力の使い方の例を3つ紹介します。
見かけの重力の使い方1:エレベーター
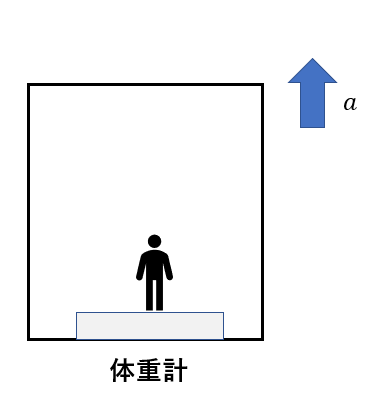
鉛直上向きに大きさ\(a\)の加速度が生じていて、その中で体重計で体重をはかります。
このとき、自分には慣性力がはたらいて、見かけの重力を考えることができます。
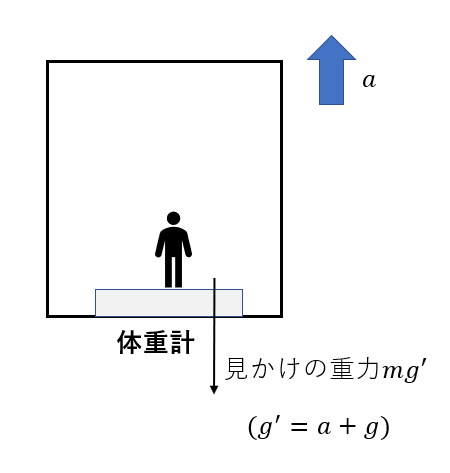
先ほど見た通り、「エレベーターの外で、重力\(mg’\)の力を受けて体重を測る」という置き換えができます。
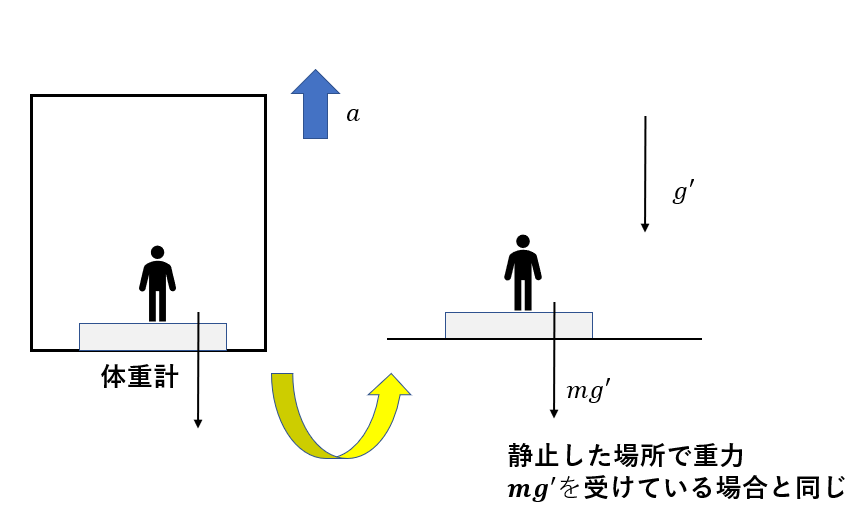
慣性力の置き換えと似た感じですね。
見かけの重力の使い方2:電車
電車も先ほど示した通りです。
ここでは「つりあい」とは違った観点で見てみます。
先ほどの電車に乗っている状況で糸を切ると物体はどのように運動するでしょう?
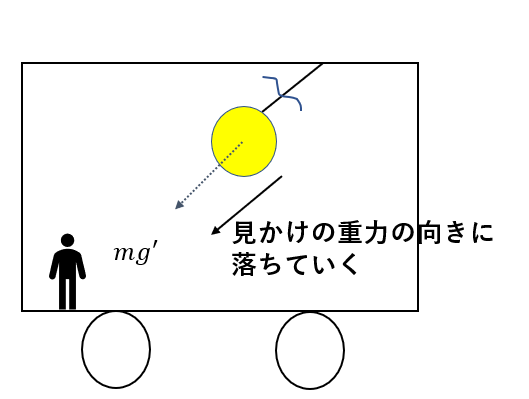
張力がなくなると、物体に働く力は見かけの重力だけになるので、その方向に落ちていきます。
(ちなみに電車の外から見た場合は右向きの水平投射になります)
もちろん、これも置き換えが可能です。
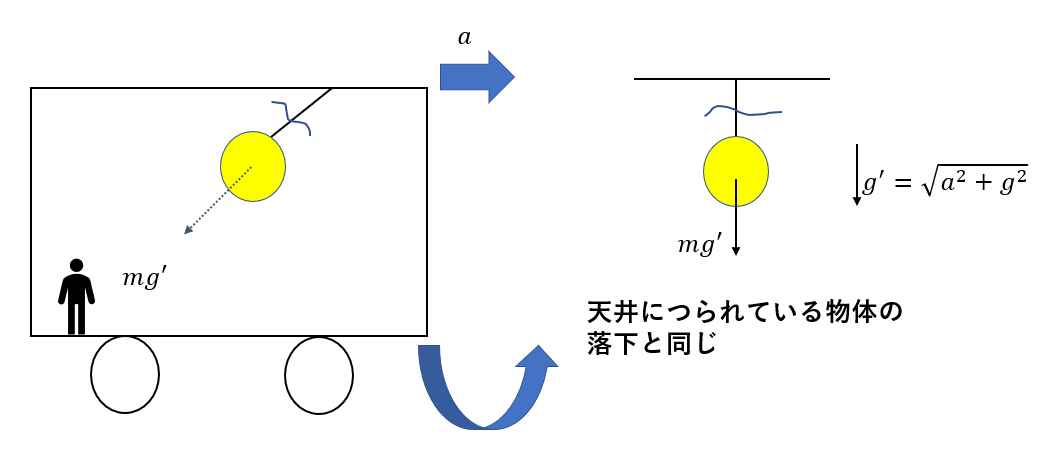
電車ではなく、ただ天井につるされて静止している状態で糸を切り、落下する物体い置き換えることができます。
ただし、その時の重力は\(mg’\)となります。
見かけの重力の使い方3:ふりこ
入試では振り子と見かけの重力が良く問われます。
と言っても、考え方は今まで全く同じです。
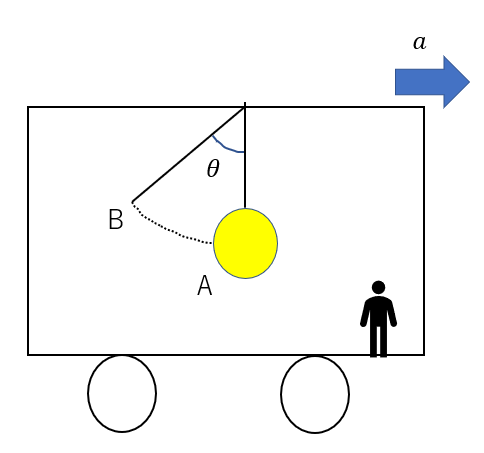
図のような電車の中で物体を見ると、AB間で単振動したという状況で、周期を考えてみます。
加速度の大きさと見かけの重力を求める
単振動する場合、中心の位置で力がつり合います。
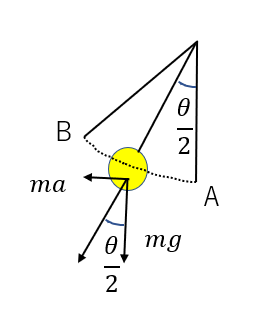
これを元に、加速度の大きさ\(a\)が求まります。
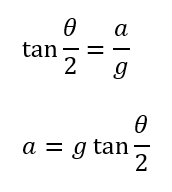
また、見かけの重力加速度の大きさも求まります。
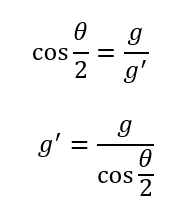
見かけの重力による単振り子
見かけの重力が求まったので、先ほどのように置き換えをします。
「ただ天井につるされて単振動する状況に置き換える。ただし、重力加速度が\(g \to g’\)に置き換わる」
ですね。
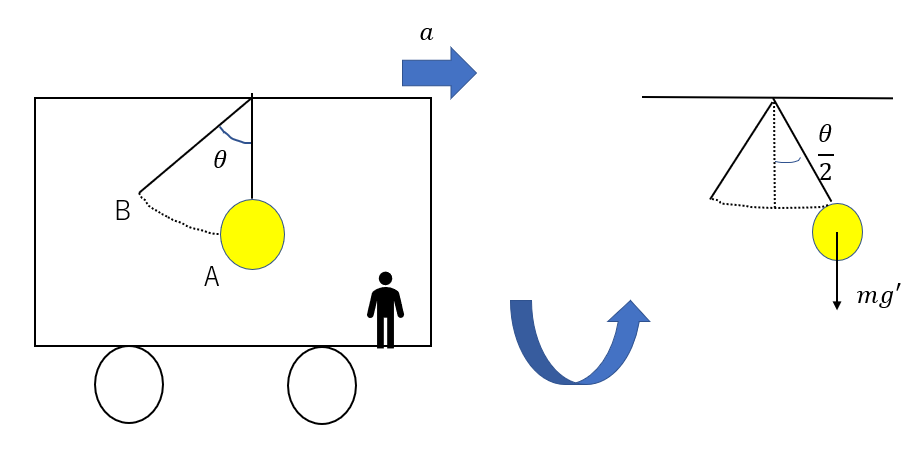
右側の単振動だと分かれば後は簡単ですよね。
運動方程式を立てて、単振動の条件を導いて、単振動の3ステップを踏めばOKです。
過程は省略しますが、周期\(T\)は
\(T = 2\pi \sqrt{\frac{l}{g’}}\)
となります。
また、物体の速さが最大になる場所も、右側の図で考えれば一目瞭然で振動の中心にきたところですよね。
電車の中で見た状況(図の左側)だと、分かりにくいですよね。しかしそれを、電車から外に出してただ天井につるされた単振動だと考えれば今までやってきた通りの方法で解くことができます。
見かけの重力や慣性力はこのような置き換えというところに威力を発揮します。
単振動について出てきたので、これに関しては以下の記事をご覧ください。
まとめ:見かけの重力は置き換えに使う
いかがでしたか?
見かけの重力は慣性力から来ているので慣性力の意味が分かっていれば大したことありません。
ただの置き換えです。
電車に乗って見ると物体が斜め方向になってしまって扱いづらいから、水平・鉛直の状況にもっていくということです。
この使い方を身に付ければ入試問題も難なく攻略できます。
それでは!ありがとうございました!
見かけの重力とは
→重力と慣性力の合力
見かけの重力の使い方
→自分が加速度運動しているのを止まった状態に置き換える。その補正として重力加速度を\(g \to g’\)にする
→まずは\(g’\)を求めよ!












