薄膜干渉をシャボン玉で理解する！条件式求めて適用せよ！
4大光の干渉講座、今回は第二弾「薄膜干渉」をやっていきますよ！
AKINORI
第一弾ではヤングの実験をやりましたね。
ヤングの実験もそうですが、
高校生で扱っている光の干渉はあくまで例です。
これが、模試とか入試にそのまま出ることはあまりないです。
干渉条件を的確に求めて、それを使って問題を解く。
この能力を身に付けてくださいね。
目次
反射による位相変化
薄膜干渉をやるうえで一つ、前提知識が必要なのでその解説からいきます。
それは
固定端反射と自由端反射です。
これは波が反射するときに、反射する点の状態で反射する様子が変わる
というものです。
固定端反射
固定端反射では、反射する点が固定されている
つまり
反射する点は動きません！
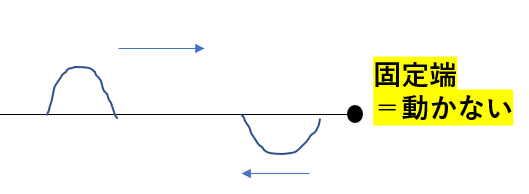
つまり、反射する点が「節」となるように波は反射しないといけませんね。
ということは
山は谷で、谷は山で帰ってきます。
難しくいうと
位相が\(\pi\)ずれる
ということです。
光で考える場合、
屈折率の大小が重要
です。
固定端は、
振動がしにくい
というイメージを持ってもらうと良いです。
そして、
振動しにくい＝屈折率が大きい
と考えてもらえれば
屈折率が
小→大
のとき
位相が\(\pi\)ずれる！！
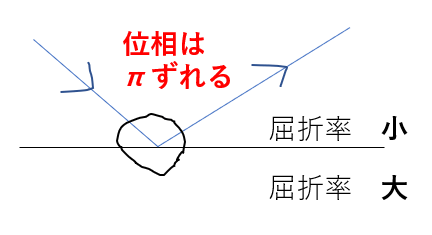
屈折率が「小→大」のとき固定端反射なんですね。
AI
自由端反射
自由端反射では、反射する点が固定されていない
つまり
反射する点は自由に動ける！
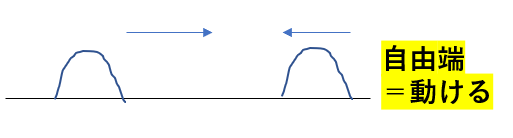
自由に動けるということは
反射点が腹となるように反射する
ということです。
ということは
山は山で、谷は谷で返る。
難しく言えば
位相はずれない
ということです。
光で考えると
自由端は
振動しやすい
というイメージを持ってもらうといいですね
振動しやすい→屈折率が小さい
ということで、
屈折率が
大→小
のとき、
位相はずれない
となります。
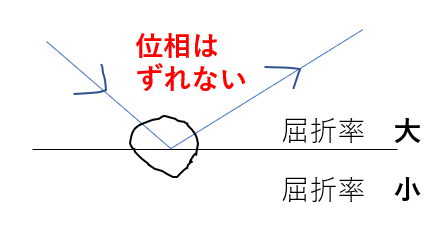
なるほど！屈折率が「大→小」のときは自由端反射になるんですね。
AI
まとめると
屈折率が・・・
- 小→大
位相が\(\pi\)ずれる
- 大→小
位相がずれない
これを考えた理由は干渉条件に影響するからなんですね。
これを踏まえて薄膜干渉を考えていきましょう。
干渉条件についてはこちら！
薄膜干渉
薄膜干渉の一例が「シャボン玉」です。
シャボン玉と関連付けて、薄膜干渉を考えましょう。
空気中に厚さ\(d\)、屈折率\(n > 1\)の油膜を張る。この油膜に同位相で平行な二つの光を照射する。光１は経路ABCDFを屈折と反射をして進み、光２は経路EDFを反射してたどる。光１の空気から油膜へ進むときの入射角を\(\theta_0\)、屈折角を\(\theta_1\)としたとき、二つの光の干渉条件を求めよ。
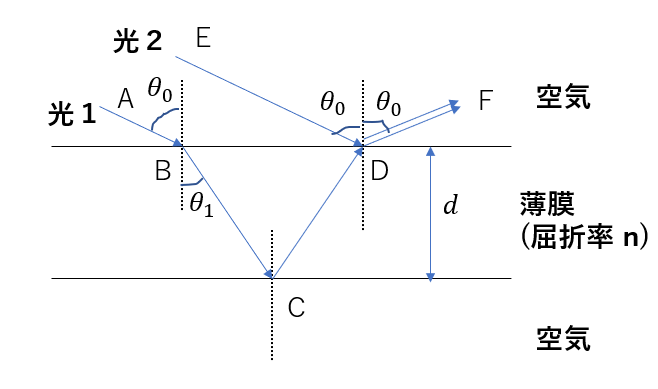
どの経路を考えれば良い？
光路差を求めればいいんですよね。・・・あれ？どの経路を考えればいいの？
AI
そこが肝心なところだよね。
AKINORI
薄膜干渉ではどの経路が差になるのかを探す必要がありますね。
とりあえず、二つほど補助線を引いてみます。
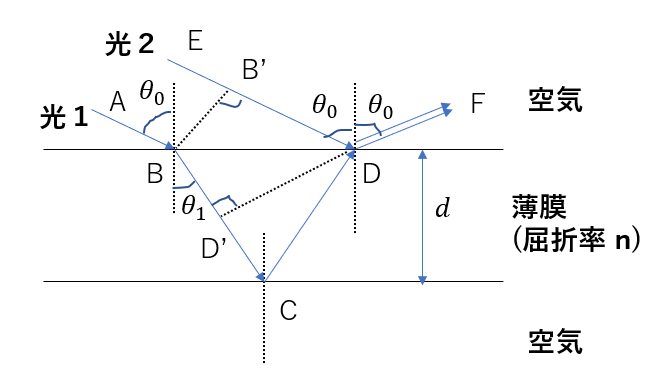
図のように、垂線BB’, DD’を引きます。
そして、次の経路を考えていきます
- ABとEB’
これは二つの波が平行なので、同じ距離進んでいます。
なので、経路差は０です。
- DF
これは、二つの光が同じ経路を進んでいるのでもちろん経路差は０です。
- BD’とB’D
これは、こちらの記事を読んでください。
屈折の法則を使ってみます。
速さが、空気中と油膜中でそれぞれ\(v_1, v_2\)だとすると
屈折の法則から
\(1・v_1 = nv_2\)
∴\(nv_2 = v_1\)
一秒間で考えたとき、
\(BD’ = v_1\)
\(B’D = v_2\)
となります。
つまり
\(n×BD’ = B’D\)
ということです。
これって・・・
光路差が同じ
ってことじゃないですか？
屈折率×距離＝光路差
ですからね。
光の干渉では経路差ではなく、光路差を考えるので、
この部分の光路差が同じなら、ここは考える必要はないということです。
つまり、考えるべき経路は
D’CD
です！！
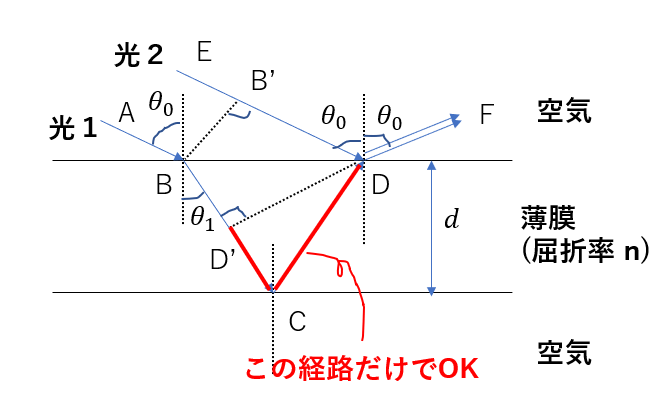
光路差を求める
D’CDの長さか・・・ちょっと工夫しないとだめそうですね。
AI
そうだね。そこで、CDを下側の境界で折り返してみよう！
AKINORI
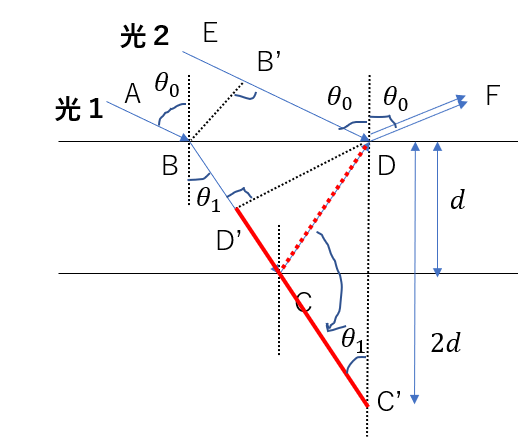
求めるのは赤の実線のD’C’ですね。
こうすると求められそうですね。
折り返しているだけなので、DC’の長さは\(2d\)ですし、
平行線の錯角から、\(\angle D’C’D = \theta_1\)です。
△D’CDに注目すればよさそうですね。
AI
なので
\(D’C’ = 2d\cos{\theta_1}\)
と表せます。
・・・
が、これは経路差です。
実際には光路差を考える必要があるので
油膜の屈折率\(n\)を掛けてあげます。
\(光路差 = 2nd\cos{\theta_1}\)
もちろん、このままでもいいのですが。\(\theta_1\)というのは測定しにくいです。一方\(\theta_0\)は自分で調整できるし、実際に測りやすいです。なので\(\theta_0\)で表しておきましょう。
AKINORI
屈折の法則から
\(1・\sin{\theta_0} = n\sin{\theta_1}\)
∴\(\sin{\theta_1} = \frac{\sin{\theta_0}}{n}\)
また、これは数学の話になるのですが
\(\sin^2{\theta_1}+ \cos^2{\theta_1} = 1\)
という公式があります。有名ですね。
これを使うと
\(\cos{\theta_1} = \sqrt{1 – \sin^2{\theta_1}}\)
∴\(\cos{\theta_1} = \sqrt{1 – \frac{\sin^2{\theta_0}}{n^2}}\)
ということで、これをさっきの光路差に代入してあげると
\(光路差 = 2d\sqrt{n^2 – \sin^2{\theta_0}}\)
と表すことができます。
干渉条件→位相変化に注意
あとは干渉条件を当てはめればいいんですね！！
AI
ちょっと待って！！今回は反射があるよね。その時の位相変化に注意だよ。
AKINORI
干渉条件は逆位相だった場合、条件が反転しますね。
ですから、反射による位相変化には注意が必要なのです。
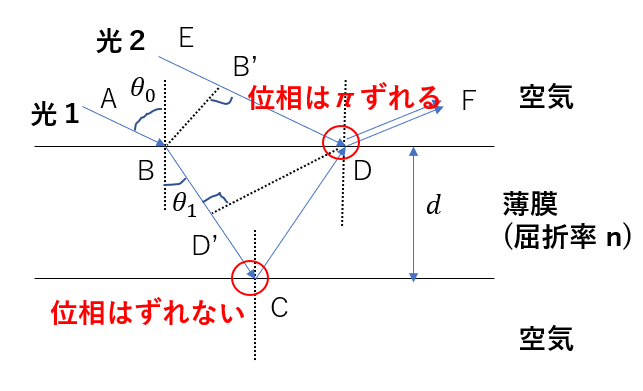
光１は点Cで反射していますね。
屈折が「大→小」なので
位相はずれません。
光２は点Dで反射していますね。
屈折率が「小→大」なので
位相が\(\pi\)ずれます。
つまり、光１，２は
互いに逆位相
なんですね。
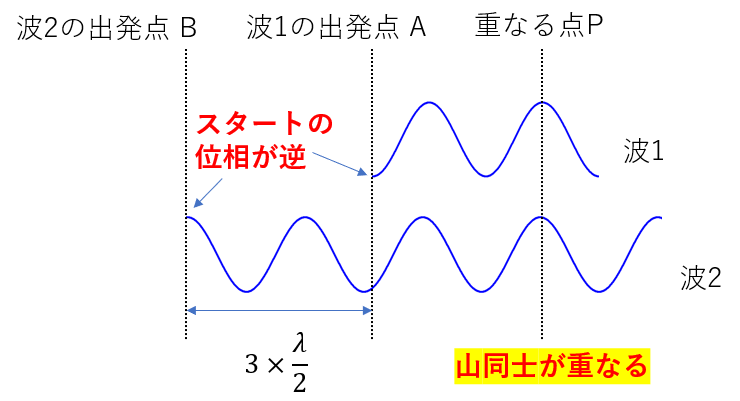
イメージはこんな感じ、
ということで、干渉条件が逆になるので、まとめると
- 明線：\(2d\sqrt{n^2 – \sin^2{\theta_0}} = (2m + 1)・\frac{\lambda}{2}\)
- 暗線：\(2d\sqrt{n^2 – \sin^2{\theta_0}} = 2m ・\frac{\lambda}{2}\)
もちろん、問題によって条件は変わりますので、覚えてはいけません。
自力で干渉を導けるようにしてくださいね。
シャボン玉の見え方がわかる？
この干渉条件からシャボン玉の見え方を考えることができます。
AKINORI
その１ 太陽光で虹が見える？
シャボン玉って見方によって虹色に見えるときがあります。
太陽光は白色光なので、いろんな色の光、つまりいろんな波長の光を含んでいます。
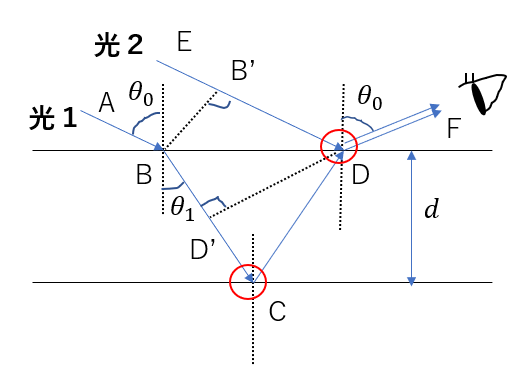
例えば、\(d\)が一定で、角度\(\theta_0\)を大きくとどうなるでしょう。
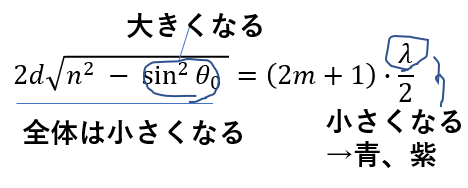
左辺は小さくなるので、右辺、つまり波長も小さくなります。
波長が小さいということは、色は青や紫に寄るってことですね。
実際はシャボン玉の油膜は場所によってことなるので、きれいな虹にはなりませんが、式からこういう解釈はできますね。
その２ てっぺんではどう見える？
もう一つ。てっぺんではどう見えるのでしょう？
油膜は重力に引っ張られて下に落ちていくので、てっぺんでは油膜がかなり薄くなります。
なので\(d = 0\)とみなしていいですね。
さて、左辺が０となるわけですが、
左辺が０となっていいのは、どちらの条件でしょう？
わかった。暗線の方ですね。\(m = 0\)とすればいいんです！
AI
もし、暗線の条件なら\(m = 0\)で成立します。
が、明線では\(m = -\frac{1}{2}\)でないと成立しません。
しかし\(m\)は整数でないといけないのでこれは反しています。
つまり、てっぺんでは
暗く見える
ということがわかります
このように、自力で干渉条件を導いて、その条件から現象を説明する。これが重要なのでよく練習しておこう！
AKINORI
はい！わかりました！！
AI
