【物理基礎】波の基本式とは?速さと振動数、そして波長の関係式v=fλ

こんにちは!オンライン塾を運営している、あっきーです
 あっきー
あっきー
波の基本式\(v = f\lambda\)の導出方法が分からない
波の基本式のイメージがはっきりしない
 リケジョになりたいAIさん
リケジョになりたいAIさん
このような悩みはありませんか?
波の基本式「v=f λ」というのは物理基礎の波のところ出てきながらも、一番大事な公式です。ですが、これを理解できていない人が多すぎます!!
波の基本公式は視覚的にイメージできるということを知っていましたか?
この記事では、波の基本公式を導出して学校では教えてくれない本当の意味を分かりやすく説明していきます。
最後まで読むことで、波の基本式そのものを理解できるのはもちろん、ドップラー効果も超簡単に理解できるようになります。
波の基本式の導出方法が分かる
波の基本式のイメージがはっきりする
ドップラー効果に応用できる
目次
波の基本式→速さ、振動数、波長の関係

物体は「位置、速度、加速度、力」の4つの量を基本的に扱っていましたね。
波でも同じように4つの量を扱っていきます。
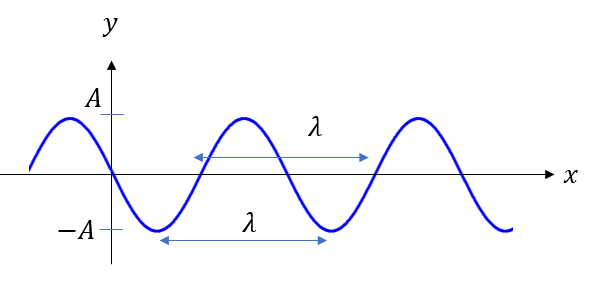
振幅\(A\):波の最大の高さ
波長\(\lambda\):波1個の長さ
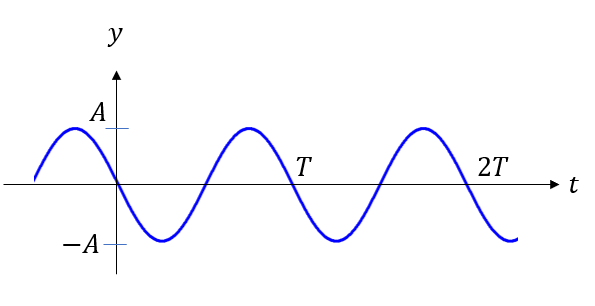
周期\(T\):ある点が1往復する時間
速さ\(v\):波が水平方向に伝わる速さ
この4つの情報を持つのが波です。実際に、この4つの情報を使って、正弦波の式を表すことができます。
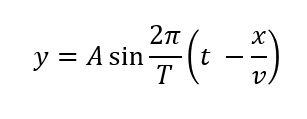
そこで、これらのうち3つ、「速さ、波長、周期(振動数)」の関係を見てみましょう。
ここで出てきた正弦波の式、そしてグラフに関してこちらを確認してくださいね。
波の基本式を導出してみる

どのように考えるかというと、波長と周期の量について見ればわかります。
波長\(\lambda\):波1個の長さ
周期\(T\):ある点が1往復する時間
どちらも波1つに関する量ですよね。
つまり、波1つが伝わる様子を考えればいいということです。
波1個に注目してみる
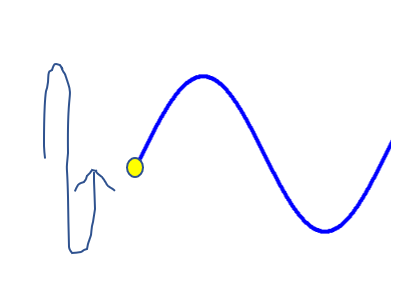
図のように、左端の点が1往復することによって波が1個現れます。
先ほど確認したように1往復するのにかかる時間が\(T\)です。
また、波1つ分の長さが\(\lambda\)です。
つまり、この波は\(\lambda\)進むのに時間\(T\)だけかかることになりますね。
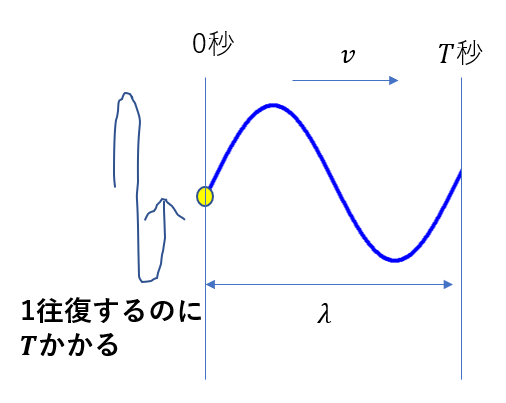
ということで、波が伝わる速さ\(v\)は次のように表せます
\(v = frac{\lambda}{T}\)
周期を振動数に変える

ここで振動数\(f \)についてですが、周期と次の関係があります。
\(f = \frac{1}{T}\)
振動数は「1秒で何回振動するか?」という意味です(単位はHz(ヘルツ))。
1秒当たりの振動回数なので “\(\frac{回}{秒}\)” ですよね。
一方周期は1回あたりにかかる時間なので “\(\frac{秒}{回}\)”です。
なので、振動数と周期には逆数の関係があるのです。
これを使って書き直せば次のような関係が成り立ちます。
\(v = f\lambda\)
これが波の基本式です。
\(v = f\lambda\)
\(v\):速さ, \(f\):振動数, \(\lambda\):波長
波の最も基本的な公式となりますのでしっかり理解しておいてください。
波の基本公式は「波の長さ」の式だった!

ここまでは波1個について考えて、「速さ×時間=距離」というのを使って波の基本式を導きました。
ですが、結果を見てみると意外な意味を持っていることがわかるのです。
それは、「波の長さ」の関係式です。
振動数は「波の個数」を表す

そのカギを握るのは振動数\(f\)です。
先ほど、振動数は「1秒当たり何回振動するか?」と言いました。
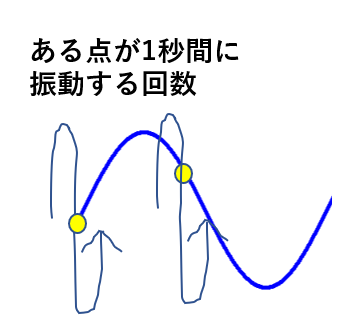
一方で、ある点が1回振動することで1つの波が表れます。
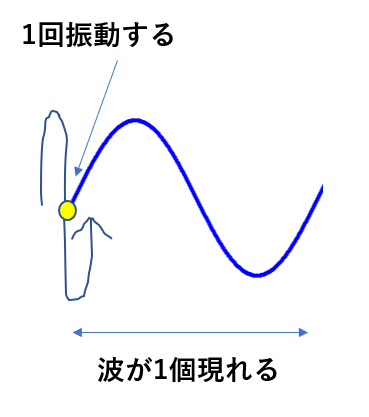
このことから振動数\(f\)の正体がわかります。
振動数\(f\) → 1秒で\(f\)個の波が出る
分かりますか?
振動数\(f\)の定義は「1秒で\(f\)回振動する」です。
そして1回の振動で1個の波が生じるわけですから、このようなことが言えるわけです。
つまり、振動数は「波の個数」を表すものだったのです。
波の基本式を見直すと・・・

これを踏まえて波の基本式\(v = f\lambda\)をもう一度見てみましょう。
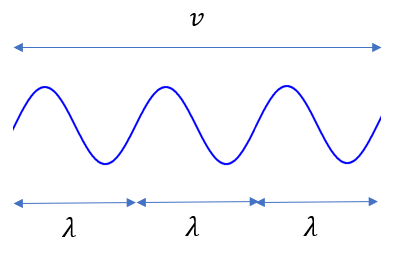
これが結論です。
\(v\)は速さです。つまり1秒で距離\(v\)だけ進むということですね(\(v \times 1 = v\) )。
\(f\)は振動数で先ほど教えた通り、1秒で\(f\)個の波を出すということです。
\(\lambda\)は波長で、波1個の長さが\(\lambda\)だということです。
ですから、「波1個の長さ\(\lambda\)の波を\(f\)個集めれば、全体の長さ\(v\)になる」ということです。
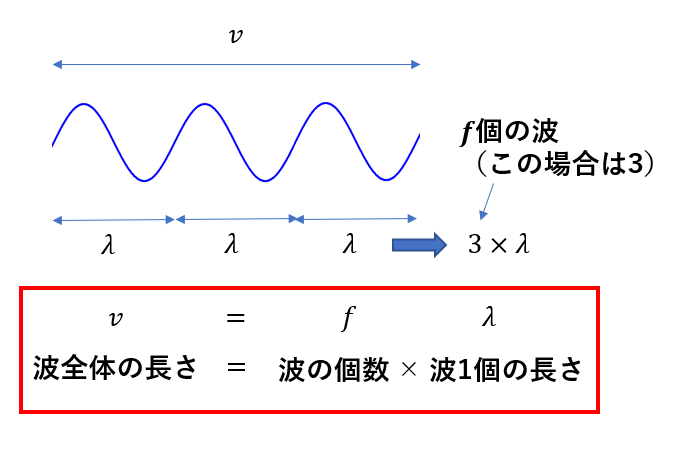
先ほど「速さ×時間=距離」という見方だったのが、「波の長さ」を表した関係に見ることができたわけです。
こちらの方が、視覚的にも分かりやすくて、イメージがしやすいですよね。
ドップラー効果では波の基本式の考え方があると良い

もちろん、問題を解くうえでは、特にこのことは意識せず、\(v=f\lambda\)という数式として使うと思います。
ですが、この振動数を「波の個数」と考えたり、\(v = f\lambda\)を「波の長さの関係式」とみなすことで、ドップラー効果がめちゃめちゃ分かりやすくなります。
波長が短くなるとか、相対速度がどうこう、など一切難しいことを考える必要はありません。
「波の個数」で一瞬で理解できます。
ドップラー効果についてはこちらで詳しく説明していますので確認してくださいね。
まとめ:波の基本式は「波の長さ」の公式

いかがでしたか?
波の基本式は物理基礎の内容ですが、なかなか奥が深いものだったと思います。
今まで\(v = f\lambda\)を呪文のように暗記していたあなたも、このように「波の長さ」と捉えることで公式の意味が分かったり、イメージができるようになったのではありませんか?
物理を伸ばすカギはまさにそこです。
今まで呪文のように覚えていた公式の意味を正しく理解します。そうすることで、どのように使えば良いのかも分かり、問題に生かせるというわけです。
暗記に頼らず、焦らずじっくり理解を深めましょう。
波の基本式
\(v = f\lambda\)
\(v\):速さ, \(f\):振動数, \(\lambda\):波長
「波の長さの関係式」と理解しよう!










