コンデンサーを含む直流回路の解き方!十分に時間が経過すると?

コンデンサーの回路問題が解ける
スイッチを入れた直後のコンデンサーの扱い方が分かる
十分に時間が経過したときのコンデンサーの扱い方が分かる
私、コンデンサーを含んだ回路だとどうしても解けなくなるんですよね・・・
 AI
AI
確かに、スイッチ操作とか入るとかなり厄介ですよね。
 AKINORI
AKINORI
回路問題はこうやって解け!という解法をこちらで紹介しました。
もちろん、ここで紹介したことは徹底してほしいのですが、コンデンサーに関してもう一つ知っておきたいものがあります。
それが「スイッチ操作」です。
よくあるのが、
コンデンサーのある含む直流回路
+
スイッチの開閉!!
これですね。
実はコンデンサーは、スイッチを入れた直後とそのあとで扱い方が変わってくるんです!!
ですからこの扱いを知っているかどうかで入試問題の難易度が変わります。
ということでここでは
スイッチを使ったコンデンサーを含む直流回路で
スイッチを入れた直後と、十分に時間が経過したときの扱い方を分かりやすく教えていきます!
目次
スイッチの操作で何が起こる?
例えばこんな回路を考えてみましょう。
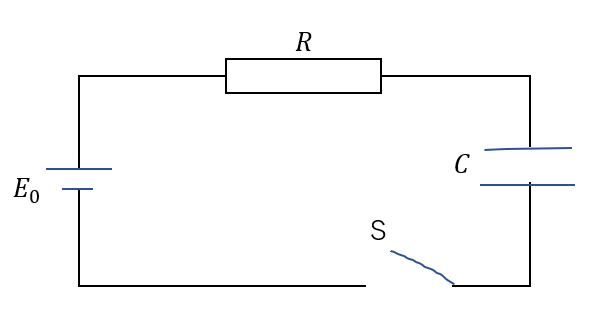
今コンデンサーには電荷が貯まっていない状態です。
ちなみに電荷が貯まっているかどうかは結構重要なので強調しておきました。その理由は後で説明します。
このようなスイッチを使うコンデンサーを含んだ直流回路では次の二つの場合を考えます。
- スイッチを閉じた瞬間
- 十分に時間が経過したとき
スイッチを閉じた瞬間

まずはスイッチを閉じた瞬間を考えます。
スイッチを閉じた瞬間の電流はどれくらい流れるでしょう?
もちろん、キルヒホッフの法則ですよね。電位差マークを書いていけばいいんですよね。電源と、抵抗と、コンデンサーと・・・
 AI
AI
ストップ!ほんとにコンデンサーには電位差が生じてるのかな?
 AKINORI
AKINORI
電流を流した直後だと、コンデンサーには電荷がまだ貯まらないと見なすことができます。
コンデンサーには\(Q = CV\)という関係がありました。
つまり、\(Q = 0\)なら\(V = 0\)ですよね。
これは、スイッチを閉じた瞬間はコンデンサーには電位差が生じない!!ということです。
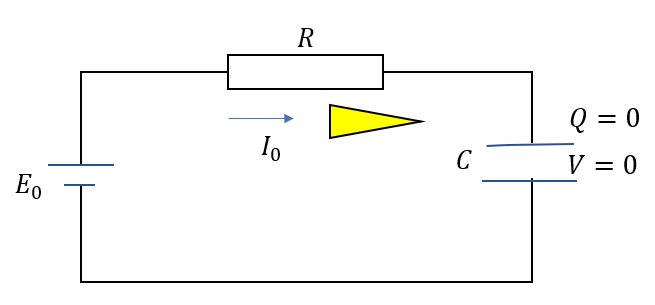
この状態でキルヒホッフの法則、つまり「一周した電位=0」を使えばいいわけです。
キルヒホッフの法則についてはこちらを確認してください
キルヒホッフの法則を使うとこのようになります。
\(E_0 – RI_0 = 0\)
∴\(I_0 = \frac{E_0}{R}\)
でも、コンデンサーって極板が向かい合ってるだけでつながってないから回路になってないですよね?そしたら電流も流れないんじゃないんですか?
 AI
AI
いい質問だね。実は大学で電磁気学を学ぶと回路中の極板間にも電流は流れている(ようにみなしていい)ことが証明できるんだ。今はあまり気にしないで大丈夫だよ
 AKINORI
AKINORI
十分に時間が経過したとき

スイッチを閉じて少し時間がたつと、コンデンサーには電荷が貯まっていきますね。
ある電荷量\(q\)が貯まったときを考えると、
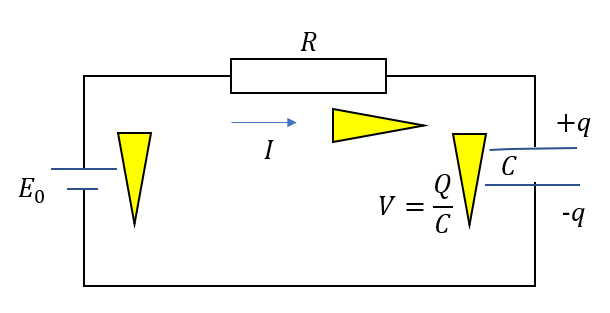
このようになります。先ほどと同じようにキルヒホッフの法則を使えばこうなります。
\(E_0 – RI – \frac{q}{C} = 0\)
∴\(I = \frac{1}{R} (E_0 – \frac{q}{C}\)
さて、時間が十分に経過するとどうなるでしょう??
えっと・・・コンデンサーに最大電荷\(Q\)たまって・・・
 AI
AI
いいね。最大電荷\(Q\)貯まるとこれ以上電流は流れなくなる。つまり電位差が\(E_0\)になるんだね。
 AKINORI
AKINORI
式を見ると、\(q\)がだんだん大きくなってやがて
\(\frac{q}{C} \to E_0\)
となるのがイメージできますよね。
そして最大電荷量\(q = Q\)となったとき
\(\frac{Q}{C} = E_0\)
∴\(Q = CE_0\)
となれば、\(I = 0\)
つまり、電流が流れなくなりますね。
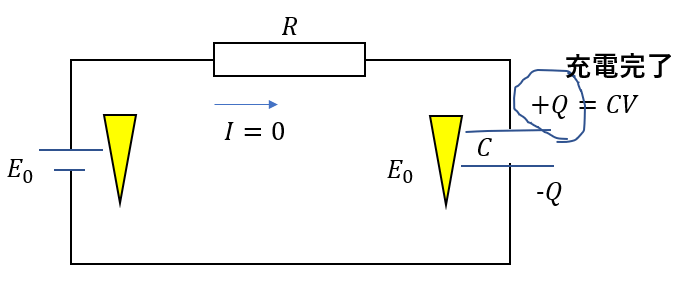
スイッチを閉じたときに気を付けるべきことはこの二つ

ここまでの話をまとめると・・・
スイッチを閉じた直後電位差が生じない。
→コンデンサーは導線として扱って良い!!
十分に時間が経過すると電流が流れなくなる。
→コンデンサーは断線として扱ってよい!!
ということがわかりますね。これはコンデンサーを含む直流回路を解く際に非常に重要なところになるのでしっかり理解しておきましょう。
コンデンサーの扱い方
\(t = 0\) → 導線扱い
\(t \to \infty\) → 断線扱い
これを踏まえて問題を解いてみましょう!
 AKINORI
AKINORI
わっかりました!!
 AI
AI
コンデンサーを含む直流回路
図のように\(R_1, R_2\)の抵抗、電気容量\(C_1, C_2\)のコンデンサーがあって、起電力\(E\)の電源がつないである。
なお、この回路は接地してある。
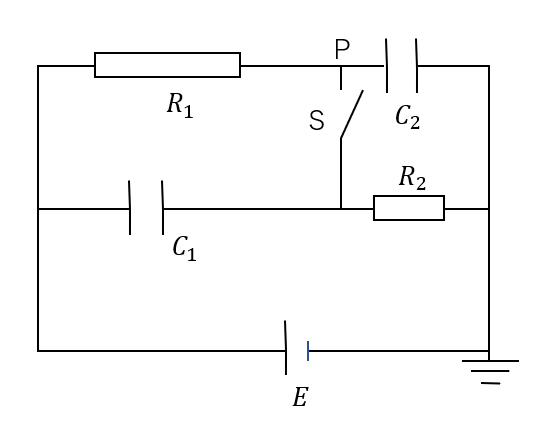
(1)スイッチが開いたまま十分に時間が経過したときの、各コンデンサーにたまる電気量と点Pの電位を求めよ。
(2)スイッチを閉じたまま十分に時間が経過したときの、各コンデンサーにたまる電気量と点Pの電位を求めよ。
先ほどのポイントを踏まえてまずは自力で解いてみましょう!以下に解説が続きます。
十分に時間が経過 → 断線扱い
(1)では十分に時間が経っているので、コンデンサーは断線扱いですね。
 AI
AI
いいね!理解できてるね。
 AKINORI
AKINORI
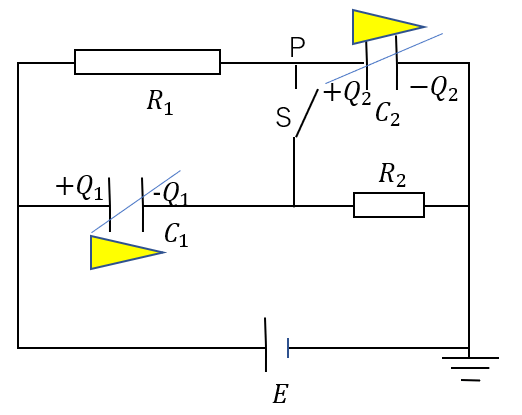
コンデンサーは断線扱いなので、図を見ればもはや回路になってませんね。つまり、電流は流れません。
よって、抵抗による電圧降下は0となり、このように電圧マークが付けられます。
キルヒホッフの法則を使って、回路を一周すればコンデンサーの電気量は求まります。
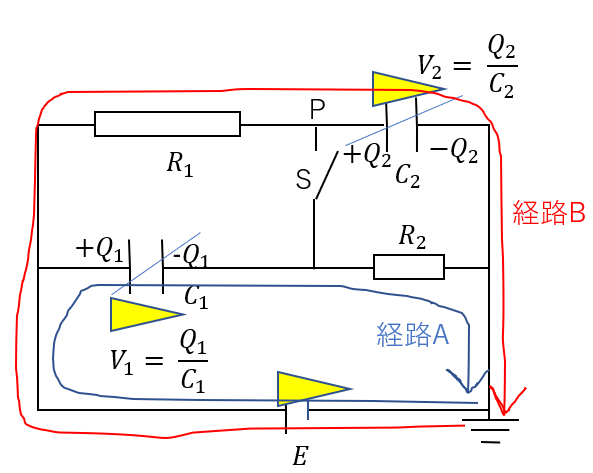
- 経路Aについて
\(E – \frac{Q_1}{C_1} = 0\)
∴\(Q_1 = C_1E\)
- 経路Bについて
\(E – \frac{Q_2}{C_2} = 0\)
∴\(Q_2 = C_2E\)
電気量は求まりました。
あとは\(P\)の電位\(V_p\)を求めます。
回路の右下にある記号は何ですか?
 AI
AI
これは接地(アース)と言って、「ここを電位を基準にするよ!」っていう意味なんだ。
 AKINORI
AKINORI
電位は必ずどこかを基準に取らないと定められません。本来はどこでもいいんですが、回路中で接地されていたら、この部分を必ず基準、つまり設置部分で\(V = 0\)としなければいけません。
「〇〇の電位を求めよ」という問題には必ず「△△を基準にする」と与えられるのでそれにしたがってください。
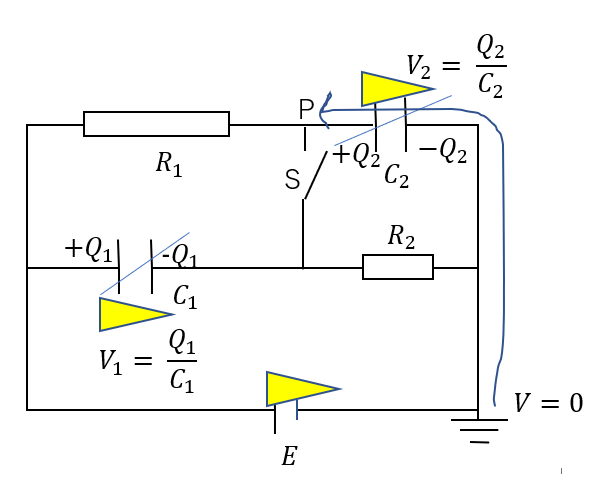
Pの電位はこの接地部分からスタートして、Pまで回路をたどっていけばOK。
キルヒホッフの法則と同じようなやり方です。
すると、\(C_2\)のコンデンサーで電位が\(V_2\)だけ上がっているのが分かりますね。
\(V_2 = E\)というのは先ほど電荷量を求めるときに分かっているので、点Pの電位は
\(V_p = E\)
となります。
(1)と同様にやってみよう
次は(2)です。
(2)も(1)と同じですね。コンデンサーは断線扱いです。
 AI
AI
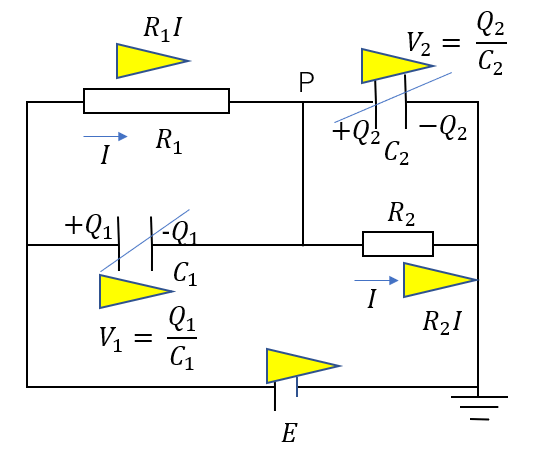
コンデンサーは断線扱いですが、スイッチを閉じているので、回路ができていますね。
なので、電流は流れます。
まず、この電流を求めてみましょう。
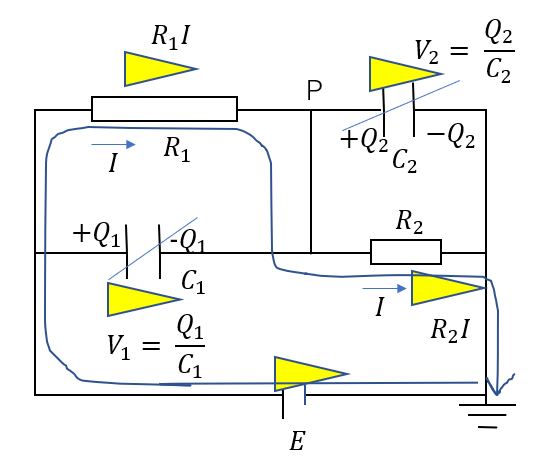
こういう経路をたどってやれば、キルヒホッフの法則より
\(E – R_1I – R_2I = 0\)
∴\(I = \frac{E}{R_1 + R_2}\)
と書けますね。
あとは、(1)と同じ経路をたどって、電荷量を求めに行きましょう!!
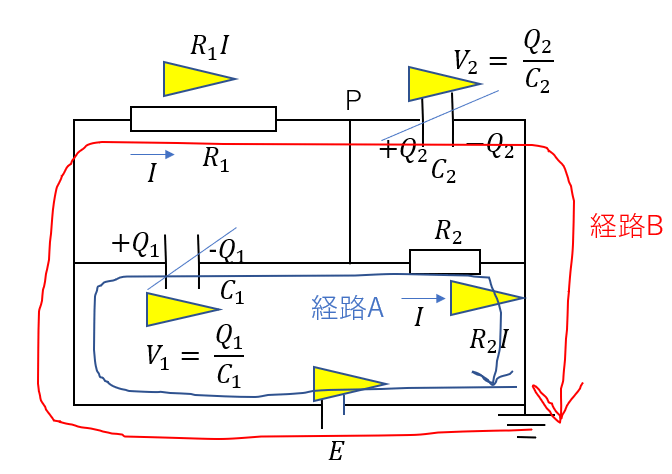
- 経路Aについて
\(E – \frac{Q_1}{C_1} – R_2I = 0\)
∴\(Q_1 = \frac{R_1C_1}{R_1 + R_2}E\)
- 経路Bについて
\(E – \frac{Q_2}{C_2} – R_1I = 0\)
∴\(Q_1 = \frac{R_2C_2}{R_1 + R_2}E\)
電荷量は求まりましたね。
あとは、Pの電位ですね。これも先ほどと全く同じです。
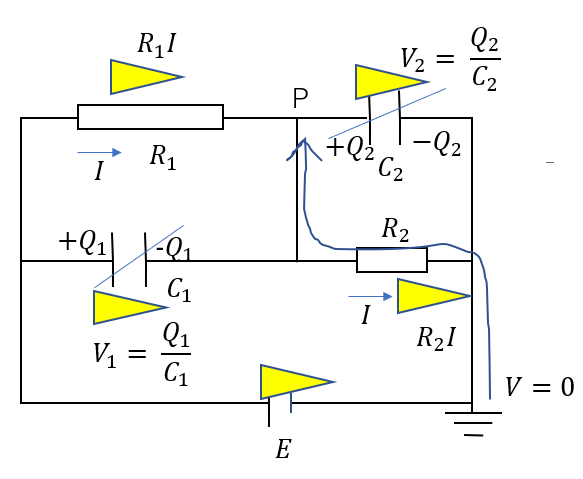
今回はこういう経路をたどってみましょう。(もちろんどんな経路でもOKです)
抵抗での電位差によって、電位が上がりますね。
なので、
\(V_p = \frac{R_2}{R_1 + R_2}E\)
が答えです。
そんなに難しくないじゃん!
 AI
AI
そう!これでも入試問題で出るから、そう考えると点が取りやすそうだね!自身ついたかな?
 AKINORI
AKINORI
コンデンサーの直流回路問題も恐くない!
![]()
いかがでしたか?
コンデンサーを含んだ直流回路ですが、難しいことは何もやっていません。基本はキルヒホッフの法則です。
それを使うにあたってコンデンサーの性質をしっかり理解していれば怖いものなんてないのです。
コンデンサーの扱い方
\(t = 0\) → 導線扱い
\(t \to \infty\) → 断線扱い
2週間で入試で勝てる電磁気ノウハウを手に入れ偏差値を10上げるオンライン塾開講中!









