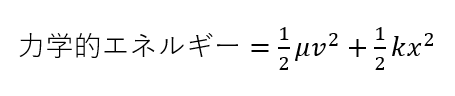二物体のばねによる単振動【換算質量を使うと楽です】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
今回は二体問題の解き方について紹介していきます。
実は、入試問題では二体問題と呼ばれるばねによって二物体が振動する運動を考えさせられます。
そして、解き方は1通りしかないのですが、その形式は問題によって様々です。
- 重心を使って考える
- 片方の物体から見て考える
今回は「片方の物体から見て考える」というところにフォーカスして考えていきたいと思います。
換算質量の意味
換算質量の使い方
目次
二体問題を解き方は重心を使うこと
初めに言っておくと、二体問題は重心を使って解くのが定石です。
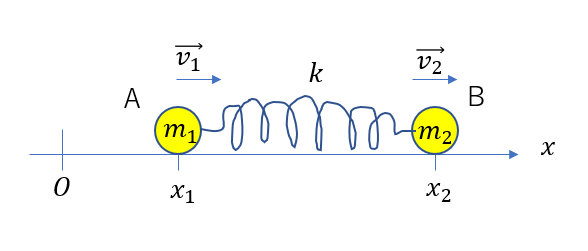
このような、二物体がばねによって単振動す問題では、重心そのものの運動と重心から見た運動に分けることで解くことができます。
今回はその別解ということで物体Aから見た物体Bの運動を見ることで解く方法を紹介します。
重心を使った二体問題の解法は以下の記事で紹介していますので見てくださいね。
二体問題の重心を使わない解法

先ほどの記事にある状況と同じものを考えます。
今回紹介する方法は「Aから見たBの運動を考える」です。
二体問題では基本的に重心や物体などから見て運動を考えます。その重心以外のパターンとしてこれを考えることができます。
二物体のばねによる単振動:換算質量
結論から言うと、AからBの運動を見ると次のような状況を作ることができます。
ばねの伸びを\(\vec{x} = (x_2 – x_1 – l)\)、相対加速度を\(\vec{a} = \vec{a_2} – \vec{a_1}\)とする。
換算質量を\(\mu = \frac{m_1m_2}{m_1 + m_2}\)と置くと、Aから見たBの運動方程式は
\(\mu \vec{a} = -k\vec{x}\)
運動方程式は簡単な単振動(水平バネ振り子)と同じになるので解きやすくなるのです。
このように表せる理由を説明していきますね。
AとBの運動方程式を立ててみる
まず、AとBに関してそれぞれ運動方程式を立ててみます。
ばねの伸び(縮み)を\(\vec{x}\)とすると、これは\(\vec{x} = ((x_2 – x_1) – l)\)となります。\(x_2 – x_1\)はばねの長さですね、そこから自然長\(l\)を引くことで伸びを表すことができます。
\(\vec{x}\)の成分が正なら「伸び」、負なら「縮み」を表します。
Aの運動方程式
Aについて運動方程式を立てます。いつも通り場合分けをしましょう。
ばねが伸びているとき\((x>0)\)のときは、力は軸と同じ向きに生じます。
つまり、弾性力の成分は正になる必要がありますね。
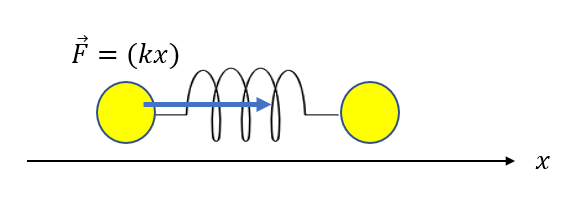
\(\vec{F} = (〇)\)の()の中身が正になる必要があるので、\(\vec{F} = (kx)\)と表せます。
次にばねが縮んでいるとき\((x<0)\)を考えると、力は軸と逆向きに働きます。
つまり弾性力の成分は負になります。
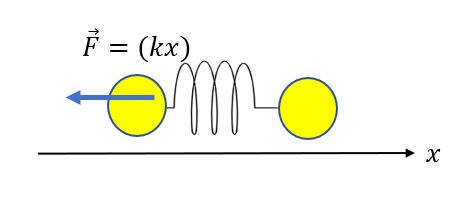
()の中身が負になりますが、\(x<0\)なのでマイナスをつける必要はなく\(\vec{F} = (kx)\)と表せます。
場合分けしても結果が同じだったので、まとめて問題ありませんね。
これを踏まえてAの運動方程式を立てると
\(m_1\vec{a_1} = \vec{F_1}\)
\(m_1a_1 = kx\)
と表せます。
Bの運動方程式
Bの運動方程式を考えます。
Aと同様に、伸び縮みの場合分けをして・・・
とやっても良いのですが、もっと簡単に考えましょう。
AとBが受けるばねの弾性力はそれぞれ作用反作用の関係にあります。
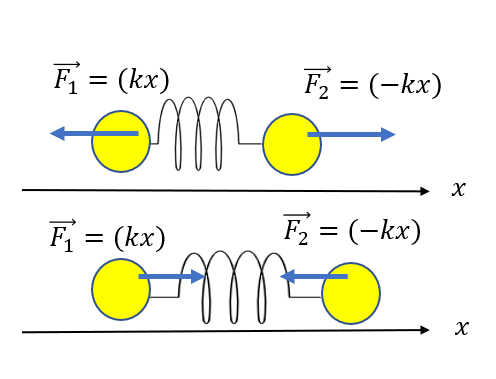
作用反作用の法則は大きさが等しく、向きが逆向きでした。
つまり、Aの力にマイナスを掛ければそれがBが受ける力になります。
つまり\(\vec{F_2} = (-kx)\)です。
これを踏まえて運動方程式を立てると
\(m_2\vec{a_2} = \vec{F_2}\)
\(m_2a_2 = -kx\)
と表せます。
Aから見たBの運動を考える→相対加速度を求める
ここから「Aから見たBの運動」を考えます。
これはAから見たBの相対加速度を求めることです。
Aから見たBの相対加速度は
\(\vec{a} = \vec{a_2} – \vec{a_1} = (a_2 – a_1)\)
と表せます。(相対加速度についてはコチラで説明しています)
先ほどの運動方程式を使って表すことができますね。
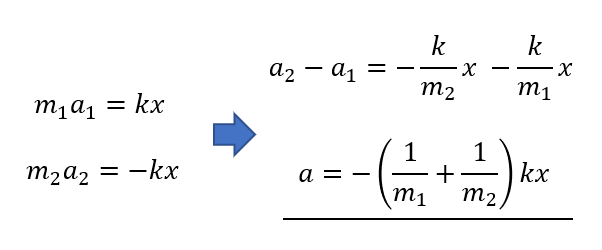
ここで\(\frac{1}{\mu} = \frac{1}{m_1} + \frac{1}{m_2}\)
つまり\(\mu = \frac{m_1m_2}{m_1 + m_2}\)と置いてみます。
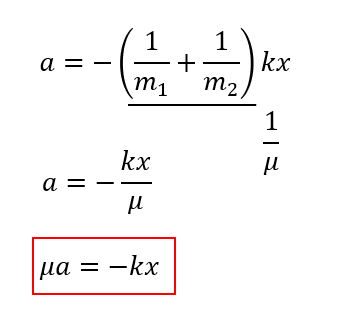
換算質量とは?
最後の式をよ~く見てください。

これはまさにAから見たBの運動方程式の形になっていますよね。
そして、この式をもう少し深く見てみると面白いことに気づけます。
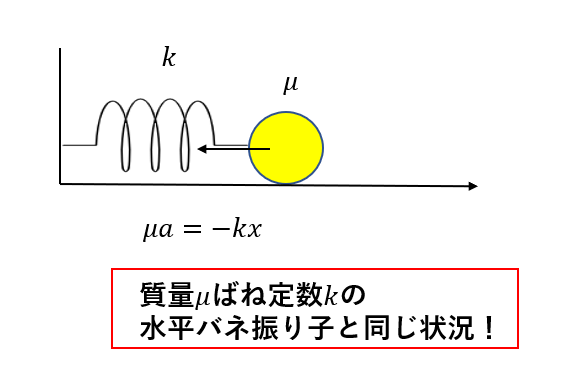
実は、Aから見たBの運動は図のような物体の単振動と同じ状況になるんです。
先ほど2物体がばねで振動していて難しそうでしたが、Aから見ることで非常に単純になりました。
この物体を置き換えたときの質量\(\mu\)を換算質量と言い
\(\mu = \frac{m_1m_2}{m_1 + m_2}\)
と表せます。
後は、単振動の運動方程式とエネルギー保存則の立て方と問題解法の解説で教えているような単振動の解法を使えばOKです。
換算質量は問題でどう使える?
この換算質量はどのように問題で使えるかというと、正直あまり使えません。
実は、入試問題では今やった流れをそのまま問われることがほとんどだからです。
今やった流れを知っていると実際に入試問題で出たときにもスムーズに解くことができて点が取れます。
逆に知らないと戸惑うので非常に難易度が難易度が上がります。
二物体のばねによる単振動:エネルギー保存則
重心で考えた場合に「重心を使ったエネルギー保存則」を考えました。
実は今回の「Aから見たBの運動のエネルギー保存則」も同様に考えることができます。
結論から言うと次のような式が得られます。
換算質量\(\mu\)、Aから見た相対速度(の成分)\(v = v_2 – v_1\)を使うと
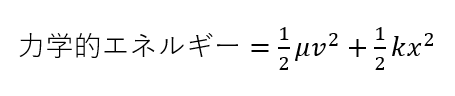
これも導出できます。
まず、物体の力学的エネルギーは次のように表せますね。
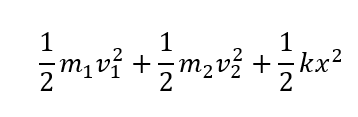
このうち運動エネルギーの方を見ていきます。
まず、この運動では外力ははたらかないので運動量保存則が成立します。

(最初の運動量の和を0としています)
また、Aから見た相対速度は次のように表せます。

これを踏まえると\(v_1, v_2\)は\(v\)を使ってそれぞれ次のように表せます。
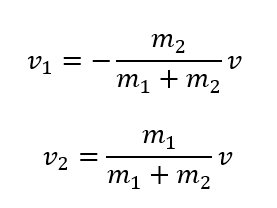
これを先ほどの運動エネルギーの式に代入して整理すれば最初に見せた式を得ることができます。
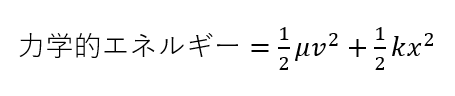
使い道はあまりありませんが、重心の場合と同じですね。
まとめ:換算質量を使った二体問題
いかがでしたか?
重心を使った二体問題の解法以外のことを教えました。
基本は重心です。なのでまずは重心を使った解き方をマスターしましょう!!
二体問題の解法
換算質量\(\mu\)を使うと次の運動方程式が立てられる

換算質量を使ったエネルギー保存則