【高校物理】微小量の扱い方。仕事などで微小変化させるときのコツ!

Akinoriさん。たまに、いやよく「微小量」を扱う問題を見るんですよ!「微小変化させると・・・」。この時ってどう対処すればいいんですか?
 AI
AI
微小量ね。今日は実際に微小量の扱い方を勉強しよう!
 AKINORI
AKINORI
高校物理では微小量を考えて議論することが多いです。
入試問題でも出るし、何かを導出、特に仕事ではこの微小量が重宝します。
入試問題ではおそらく誘導があるんですが、ある程度知識があるといきなり出てきてもスムーズに対応できるので、今日は微小量の扱い方をマスターしていきましょう!!
目次
微小量って何?
そもそも微小量っていうのは問題ではこう書かれています。
「微小距離\(\Delta x\)だけ変化させると・・・」
これがまさに微小量です。
本当に小さい数ということです。
0.00001
みたいな数だと考えてもらってOKです。
\(\Delta \)には「微小変化」っていう意味合いがあるので、微小量にはよく\(\Delta \)を使います。
では、この微小量をどう扱っていけばいいのか?
いまからすべて公開します!!
微小量その1:面積計算
じゃあ、実際に微小量を扱う練習をしてみよう!まずはこれ。「面積計算」です。
 AKINORI
AKINORI
まずは
面積計算
です。
面積と言えば仕事ですよね。
というわけで、仕事を微小量をつかって求めてみます。
1次の微小量
例として「ばねの弾性エネルギー」を考えてみましょう!!
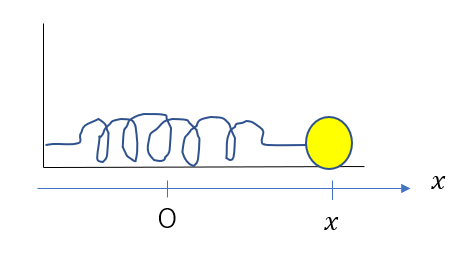
今、ばね定数\(k\)の物体が位置\(x\)、つまりばねが\(x\)だけ伸びている場合を考えます。
ばねの力が原点までした仕事を\(W\)とすると、
エネルギー原理より
\(0 + W = \frac{1}{2}mv^2\)
ですね。
エネルギー原理についてはこちらで!!
そして、右辺は「エネルギー」ですので、このばねがした仕事\(W\)もエネルギーと考えたいわけです。
よって、この\(W\)を「ばねの弾性エネルギー」と定めましょう!!
じゃあ、具体的に\(W\)を求めたいんですが・・・
「力×距離」としちゃだめなんですよね。ばねの弾性力は伸びで変わっちゃうから。
 AI
AI
お!よく気づいた!
 AKINORI
AKINORI
ばねの弾性力の大きさは
\(F = kx\)
と書けます。
\(x\)はばねの伸びですね。
ってことは、物体が動くたびにばねの弾性力は変化しちゃうわけですよ!!
そこで、登場するのが「微小量」です。
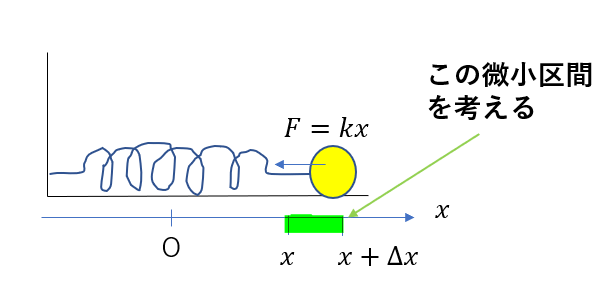
弾性力が\(x + \Delta x\)から\(x\)までにする仕事を考えましょう!
まず、動く向きと力の向きが同じなので、仕事は正。
ここまではOKですね。
そして、この区間の弾性力の大きさなんですが
この場合
一定とみなして良いですね
なるほど!\(\Delta x\)は微小量なので、\(\Delta x\)程度の変化だったら無視していいんですね!
 AI
AI
ばねの伸びが0.0000001
だけ変わったとしても、弾性力はほとんど変化しないですよね。
なので、この区間では
\(F = kx\)
という一定の大きさの力が働きます。
力が一定なら「力×距離」で表せますね。
なので、この区間にした仕事\(\Delta W\)は
\(\Delta W = kx\cdot \Delta x\)
さて、これをグラフにもっていきたいと思います。
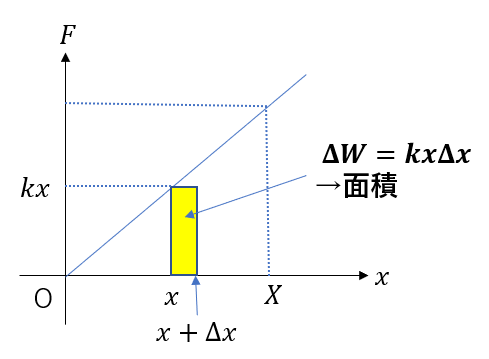
今求めた\(\Delta W \)は図の長方形の面積と同じですよね?
一か所しか考えていませんが、これをいろんな区間をとってみると、似たような長方形が階段状に並びます。

これを\(oからX\)まで並べれば、求めたい仕事が求まりそうですね。
実際には\(\Delta x\)はとにかく小さく、つまり\(\Delta x \to 0\)を考えないといけません。
すると、\(0からX\)までの三角形になりますよね?
この面積を求めると
\(W = \frac{1}{2}kX^2\)
となるわけです。
というわけで、改めて\(X\)を\(x\)に置き換えてあげれば、弾性エネルギーは
\(U_k = \frac{1}{2}kx^2\)
とあなたが知っている式になるわけですね。
なるほど!
 AI
AI
ちなみにこの考え方がまさに積分です。詳しくは「区分求積法」で調べてください。数Ⅲでもやります。
 AKINORI
AKINORI
ポイントは
微小量変わっても、一定だよね!!
ってことです。
二次の微小量
では同じように、今度は万有引力の位置エネルギーを考えてみましょう!
 AKINORI
AKINORI
全く同じように、エネルギー原理を使うと
\( 0 + W = \frac{1}{2}mv^2\)
なので、やっぱりこの\(W\)をエネルギーとして扱いたいわけですよ。
ということで万有引力がした仕事を求めます。
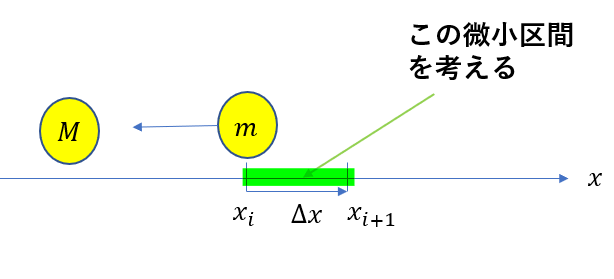
万有引力の大きさは
\(F = G\frac{Mm}{r}^2\)
と表せます。
\(r\)が二物体の距離なので、やっぱり場所によって変化します。
なので、単純に「力×距離」と表せませんね。
そこで、図のように、
正の向きに\(\Delta x\)だけ動かすときの万有引力のした仕事を考えます。
まず、力の向きと動く向きが逆なので、仕事は負です。
そして、この微小区間を考えると、やっぱりほんのちょっとの変化だったら
\(F\)は一定と考えても良いですよね?
つまり
\(F = G\frac{Mm}{x_i^2}\)
としてもOK
ということです。
なので、「力×距離」で仕事\(\Delta W\)を求めると
\(\Delta W = -G\frac{Mm}{x_i^2}\Delta x\)
これは次の長方形の面積です。
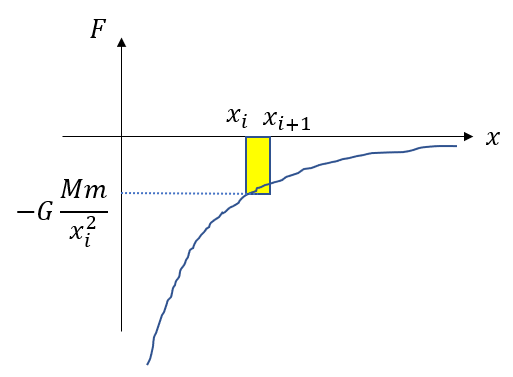
面積にプラスマイナスはないのですが、図のように\(x\)軸より下の面積を負と定めます。
さっきのようにこれをならべて\(\Delta x \to 0\)を考えればいいのですが、さっきのような三角形のような図形にはなりませんよね。
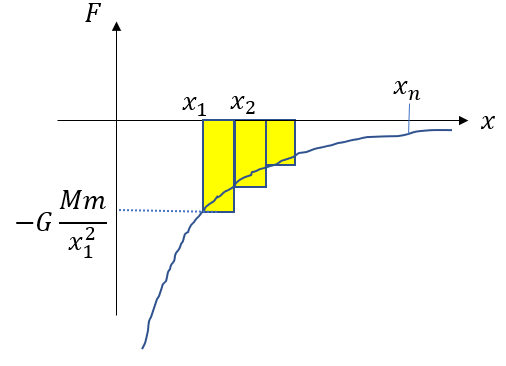
そこで、こう考えます。
\(x_i, x_{i+1}\)はほとんど変わらない量ですから。
\(x_i^2 = x_ix_{i+1}\)
と考えても良いですよね?
すると仕事は
\(\Delta W = -G\frac{Mm}{x_ix_{i+1}}(x_{i+1} – x_i)\)
\(\Delta W = -GMm(\frac{1}{x_i} – \frac{1}{x_{i+1}}\)
これを踏まえて
位置\(x_0\)をスタートとして\(x_n\)まで足していけば
\(x_0からx_n\)まで万有引力がした仕事が導けます
\(W = -GMm \{ (\frac{1}{x_1} – \frac{1}{x_2}) + (\frac{1}{x_2} – \frac{1}{x_3}) + … + (\frac{1}{x_{n-1}} – \frac{1}{x_n})\}\)
∴\(W = -GMm(\frac{1}{x_1} – \frac{1}{x_n})\)
こう表せます。
基準点を無限遠、つまり\(x_n \to \infty\)に取れば、
\(\frac{1}{x_n}\)は消えます。
というわけで、改めて\(x_1 = r\)として、整理すると
\(U = -\frac{GMm}{r}\)
これが万有引力のエネルギーです。!!
ちょっと難しい近似があったけど、やってることは「微小量なら一定でいい」ってことを使っただけですね。
 AI
AI
そうだね。これは電位のところでも使える話だよね。
 AKINORI
AKINORI
*ちなみに
きれいな図形だから面積が求まらないという話でしたが、これは積分なので、積分ができれば後半の話はいらないです。
数Ⅲを習っていればできる積分ですが、高校物理では積分をあまり使いたくないので、こういうことをやりました!!
微小量で使える近似式
では、最後に微小量が出てきたときによく使う近似式を教えておきます。これは問題文に書かれることですが、確認しておきましょう!!
 AKINORI
AKINORI
\((1 + \alpha)^n\)の近似
一つ目はこれです。
\(\alpha\)が1より十分小さいとき
\((1 + \alpha)^n = 1 + n\alpha\)
例えば、\(X\)が\(\Delta x\)よりも十分に大きい\((X << \Delta x)\)というとき、
\(X + \Delta x)^2\)
=\(X^2(1 + \frac{\Delta x}{X})^2\)
Xは\(\Delta x\)より十分大きい\(\frac{\Delta x}{X}\)は1より十分小さいと言えます。
つまり
\(X^2(1 + 2\frac{\Delta x}{X})\)
\(=(X^2 + 2X\Delta x\)
と書けます。
微小量同士の掛け算は0
これは例えば微小量\(\Delta x\)について
\((\Delta x )^2 = 0\)
が成り立ちます。
\(\Delta x\)はただでさえ小さいのに、それをもう一回掛けたらとんでもなく小さいですね。
つまり、無視していいってことです。
\(\alpha\)が十分小さいときの三角関数
これはsin, cos, tanについてですが、
これにも近似式が成り立ちます。
\(\alpha\)が十分に小さい、つまり0に近いときは、
\(\sin{\alpha} = \tan{\alpha} = \alpha\)
\(\cos{\alpha} = 1\)
いかがでしたか?
微小量を使った話はいろいろ出てきます。
重要なのは
微小量を使うと何かが一定
これを意識していくと良いですね。








