【物理】遠心力とは？公式を慣性力から求める
こんにちは！オンライン塾を運営している、あっきーです
あっきー
遠心力の意味がよくわからない
遠心力がなんで向心力と同じなの？
遠心力の公式の求め方が分からない
リケジョになりたいAIさん
このように悩んでいませんか？
実は遠心力はここで紹介する慣性力の知識を使えば公式を求めることができます。
この記事では、遠心力の公式を授業では教えてくれない慣性力の意味から求めていきます。
最後まで読むことで、遠心力の意味と公式が理解できるとともに、慣性力の使い方も分かるようになります。
遠心力の意味を理解できる
遠心力と慣性力の関係が理解できる
遠心力の公式が導出できるようになる
遠心力を問題で使う方法を知れる
目次
遠心力は慣性力の一種
遠心力は結論から言うと慣性力の一種です。
ですから、慣性力について知識をしっかりつければ遠心力はすぐに理解できます。
こちらの記事の内容をまとめると
慣性力は、
観測者が加速度運動しながら物体を見るときに働く仮想的な力
です。
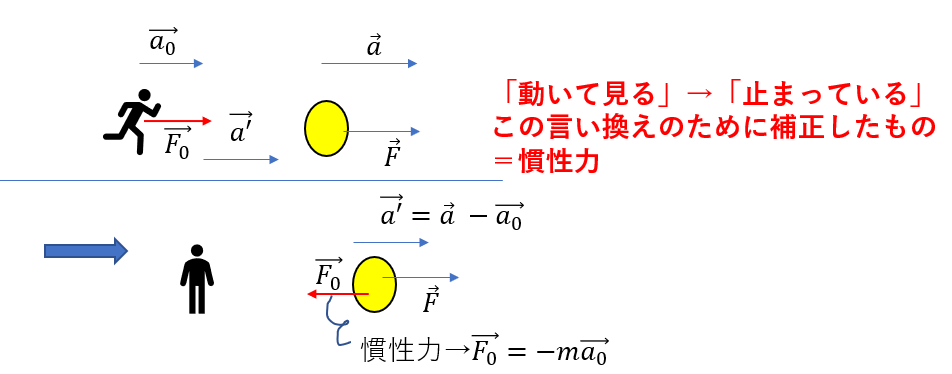
本当は動いて見ているんだけど、あたかも自分が止まって見るかのようにみなすために、何かを補正するのでした。
その補正するものが慣性力というもので
\(\vec{F_0} = – m\vec{a_0}\)
と書くことができます。
\(\vec{a_0}\)は観測者の加速度だったので、それにマイナスがつくということは
自分の加速度の向きとは逆向きに物体に力を押し付ける
ということになります。
まさに「補正」ですよね。
遠心力とは？→円運動での慣性力
これを踏まえて遠心力を考えてみましょう。
遠心力は円運動において慣性力を適用したものです。
円運動に関してはこちらを確認ください
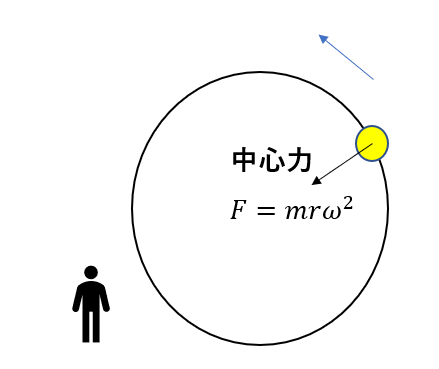
円運動は中心向きの合力（中心力）が働くことで起こる運動でした。
中心力がはたらくということは
中心向きに加速度が生じていますね。
運動方程式\(m\vec{a} = \vec{F}\)から、合力\(\vec{F}\)の向きに加速度\(\vec{a}\)が生じていることはわかると思います。
円運動の場合はこの加速度の大きさが
\(a = r\omega^2 = \frac{v^2}{r}\)
でした。
ですので、中心力の大きさは運動方程式を使えば
\(F = mr\omega^2\)
となります。
物体と同じように運動するとどうなる？
今まで円運動のというのは自分が地面に立って見ていました。
観覧車を外から眺める感じです。
ですがここでは物体と同じ運動をしながら見てみましょう。
つまり、観覧車に乗って自分が乗っている席を見るということです。
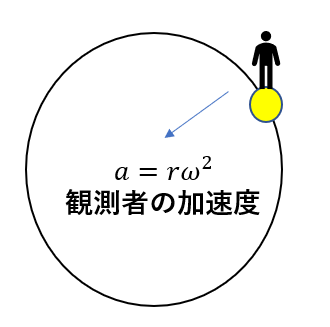
観測者は円運動をしていますから加速度が生じています。
中心向きに大きさ\(a = r\omega^2\)でした。
そして慣性力が働きます。
\(\vec{F_0} = -m\vec{a_0}\)
つまり、
自分の加速度と逆向きに、大きさ\(ma_0\)の力が生じるわけです。
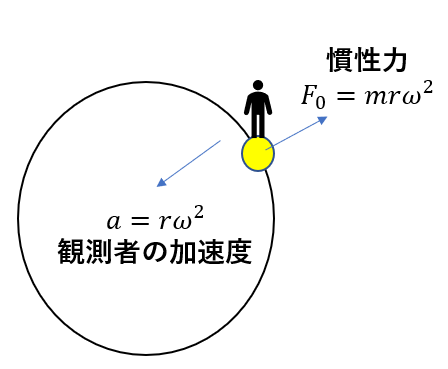
この慣性力を特別に遠心力と名付けたのです。
遠心力の式は向心力と同じなのはなぜ？
あれ？遠心力は向心力と同じ式で表されてる？
リケジョになりたいAIさん
よく見ると遠心力の式は、向心力と同じ形になっています。
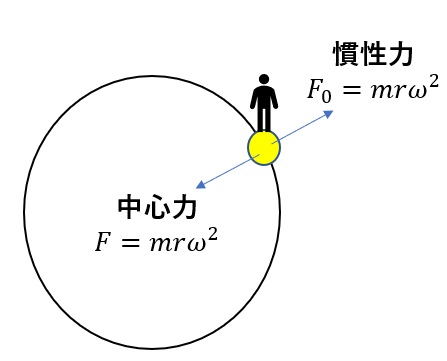
これは当然です。
地面に止まって立って見たら、もちろん物体は円運動しています。
ところが自分も同じ円運動をしながら物体を見たら・・・
止まって見えますよね？
観覧車に向かい合って座って相手を見つめても相手は動かないですよね。
止まって見えるということは力がつり合っているということです。
もともと向心力がかかっていたので、これと同じ大きさで逆向きの力がはたらくわけです。
ですから、遠心力は向心力と同じ式になって当然ということです。
遠心力はどうやって使う？
この遠心力って使い道あるんですか？ぶっちゃけ使わなくても解けますよね？
リケジョになりたいAIさん
遠心力、というより慣性力は基本的に使わなくても解けます。
根本は運動方程式なので、慣性力を使うことと普通に運動方程式を立てることは大して差はありません。
なので、好きな方で解ければいいです。
遠心力（慣性力）を使うメリットとしては、一見複雑そうな状況も単純化できることです。
先ほども見たように、円運動している→静止しているに置き換えることができましたよね。
このように運動を簡単にすることができるので、イメージもしやすくなりミスも減ります。
このように使ってみるといいでしょう。
まとめ：遠心力を公式として覚えるな
いかがでしたか？
慣性力の本質をつかんでいれば、遠心力なんて大したことないと分かったでしょうか？
遠心力を公式として教えられた方もいると思いますが、公式なんてありません。
今回説明したように、1個1個たどっていけば式が出ます。
すべてを暗記で終わらせようとせず、必ず正しく理解して、正しく使えるようにしましょう。
遠心力
円運動において慣性力を適用したもの
