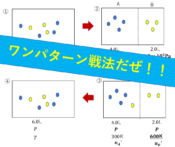
気体の混合問題でエネルギーの和が一定に保たれる理由は?
こんにちは。
こういう問題を見たことありませんか?
(セミナー物理2016 例題40)
この解説を見ると「A,Bの気体の内部エネルギーの和は保存される」
と書いてありますよね。
あ!これ気になってました。直感的にそんな気がしますが、しっかり理解したいです。
 AI
AI
もちろん、直感的に理解しても良いです。高校では説明できないことも多くありますからね。
とはいえ、できることならしっかり理解しておいた方が、初見問題でも使えます。
なので、今回はこの「エネルギーの和は保たれる」という理由を式で説明していきます。
目次
気体を混合してみると・・・

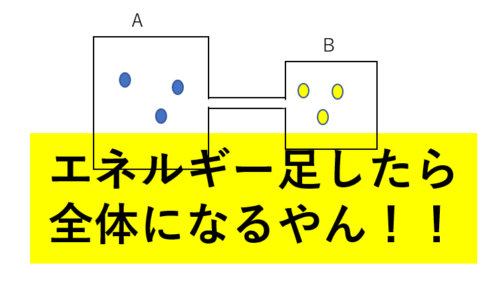
圧力、体積、温度がそれぞれ\(P_A , V_A, T_A\)の気体A, \(P_B, V_B, T_B\)の気体Bがある。はじめは図のような容器で密閉されていて、コックが閉まっている。コックを開いて十分時間が経ったときエネルギーについてどんな特徴があるか考えよう。

熱力学ではまず二つの公式を考えますね。
状態方程式と熱力学第一法則です。
今回はエネルギーについて考えるので第一法則を考えるのが良いですね。
熱力学第一法則についてはこちらを確認してください。
それぞれの気体で第一法則を考える

それぞれの気体の変化を追ってみましょう。

コックが開くと圧力、体積、温度がそれぞれ変化するので、当然ながらエネルギーも\(U_A’\)に変化します。
熱力学第一法則より
\(Q_A = \Delta U_A + W_A\)
しかし、今回は熱のやり取りがありません。
そのため\(Q_A = 0\)となります
\(\Delta U_A + W_A = 0\)
同じようにBについても考えます。

Bも変化が起こりますが、体積は容器全体なのでAと同じ\(V\)で、時間が経つとAとBの温度は同じになるのでAと同じ\(T\)になります。
圧力はAと同じにはならないので\(P_B’\)としておきます。
同様に第一法則を立てると
\(Q_B = \Delta U_B + W_B\)
ですが、こちらも同じく\(Q_B= 0\)となるので
\(\Delta U_B + W_B = 0\)
という関係式が得られます。
ここで、\(W_A\)と\(W_B\)の関係を見てみましょう。
コックを開くとそれぞれの気体がぶつかっていきますよね。

図のように、
Aの気体がBの気体に仕事\(W_A\)をし、
Bの気体がAの気体に仕事\(W_B\)をしますね。
\(W_A\)はAがした仕事なので
\(-W_A\)はAがされた仕事になります。
マイナスを受けると向きが変わるんですね。
Aがされた仕事は図のようにBがした仕事\(W_B\)だと分かっていますから
こんな関係が見えてきます
\(-W_A = W_B\)
なるほど。互いに仕事をし合うから、足し合わせると0になる関係があるんですね。
 AI
AI
これを踏まえて先ほど導いた二つの式
\(\Delta U_A + W_A = 0\)
\(\Delta U_B + W_B = 0\)
を足してみると
\(\Delta U_A + \Delta U_B = 0\)
このようになります。(この足すという行為は「混合する」と関連していますね)
あ!だんだん見えてきました!!
 AI
AI
エネルギーの和=一定
改めて
\(\Delta U_A = U_A’ – U_A\)
\(\Delta U_B = U_B’ – U_B\)
と置き換えると
\(U_A’ – U_A + U_B’ – U_B = 0\)
\(U_A’ + U_B’ = U_A + U_B\)
これはつまり
(混合後のエネルギーの和)=(混合前のエネルギーの和)
となってますね。
これで最初の解説通り「エネルギーの和は一定」ということが示せました。
混合後のエネルギーってどう表せる?

あれ?でも使い勝手悪くないですか?「混合前のエネルギー」は求めやすいけど「混合後のエネルギーの和」はちょっと面倒じゃないですか?
 AI
AI
確かにそうですね。
\(U_A’\)と\(U_B’\)をそれぞれ求めないといけないわけですが、それって面倒です。
できることなら一気に求めてやりたいですよね。
その方法をお見せしましょう。
内部エネルギーというのは単原子分子理想気体の場合
\(U = \frac{3}{2}nRT\)
と表せます。
そして状態方程式\(PV = nRT\)を使えば
\(U = \frac{3}{2}PV\)
とも表すことができます。
まず単原子分子で考えてみましょう。

このように変化する状況を考えると混合後のエネルギーの和はこう表せます。
\(U_A’ + U_B’ = \frac{3}{2}P_A’V + \frac{3}{2}P_B’V\)
つまり
\(U_A’ + U_B’ = \frac{3}{2}(P_A’ + P_B’)V\)
この\(P_A’ + P_B’\)に注目してみましょう。
これは混合後の「Aの圧力とBの圧力の和」
ですよね。これってつまり
混合後の全体の圧力ですよね。
つまり混合後の全体の圧力を\(P\)と改めて置けばエネルギーの和は
\(\frac{3}{2}PV\)
と表せます。
\(P\)は全体の圧力、\(V\)は全体の体積なので、これは
A,Bの気体を一つに見た「全体のエネルギー」となります。
したがって
(混合後のエネルギーの和)=(全体のエネルギー)
と言い換えることができるんですね。
ということで混合する場合
(全体のエネルギー)=(混合前のエネルギーの和)
と言い表すことができます。
具体的に式にしてみれば
\(\frac{3}{2}PV = \frac{3}{2}P_AV_A + \frac{3}{2}P_BV_B\)
\(PV = P_AV_A + P_BV_B\)
となりますね。
全体のエネルギーだったら問題文の情報から簡単に導くことができるので
これなら使い勝手がよさそうですね。
単原子分子じゃなくても使える

あれ?でも今は単原子分子という場合で考えたじゃないですか?ほかの場合だとダメになっちゃうんじゃ・・・
 AI
AI
良いところに気づきましたね。
今のは単原子分子の場合の話でした。
ですが、ラッキーなことにこれはどんな気体でも使える技なんです。
単原子分子理想気体では内部エネルギーは
\(U = \frac{3}{2}nRT\)
でした。
しかし、例えば二原子分子の場合
\(U = \frac{5}{2}nRT\)
となります。
気体分子の構造で式が変わってしまうんですね。
ですが、どんな構造であっても定積モル比熱\(C_V\)という定数を使って内部エネルギーはこう表すことができます。
\(U = nC_V T\)
単原子分子では\(C_V = \frac{3}{2}R\)
二原子分子では\(C_V = \frac{5}{2}R\)
となります。
この定数が変わるだけなので、特に問題なく
(全体のエネルギー)=(混合後のエネルギーの和)
は成り立つのはもちろんです。
そして次がポイントです。
先ほどこの計算を実際にやっていました。
\(\frac{3}{2}PV = \frac{3}{2}P_AV_A + \frac{3}{2}P_BV_B\)
\(PV = P_AV_A + P_BV_B\)
これを見ると\(\frac{3}{2}\)という部分がきれいになくなって、圧力と体積の情報のみになりましたよね。
この\(\frac{3}{2}\)というのは・・・・
そうです。
単原子分子の定積モル比熱の\(\frac{3}{2}\)ですよね。
このように、気体の構造で異なる値を持つ\(C_V\)が計算の途中できれいになくなってしまうんです。
二原子分子でも\(\frac{5}{2}\)が結局消えてしまうんですよ。
結局消えてしまうということは
どんな気体でも使える
ということなんです。
「単原子分子理想気体」という断りが問題文になくて、内部エネルギーを表せなくても、問題なく解けるってわけですね。圧力と体積の情報さえあれば可能ということなんですね。
 AI
AI
これで混合・分離の問題はバッチリ

いかがでしたか?
混合でできたことはもちろん分離をする際にも使えます。
なので、複数の気体を混ぜたり離したりする問題はもう「エネルギー=一定」というのが使えればOKということです。
他に解法なんていりません。これですべてに通用するので、後は問題で確認していきましょう。
どんな気体であっても混合・分離のときは
(混合気体の全体のエネルギー)=(混合前の各気体のエネルギーの和)
が使える!
*\(U = nC_VT\)の\(C_V\)の値が気体によって異なり計算ができないように見えるが、計算途中で\(C_V\)が必ず消えるので、どんな気体でも使える!!
→つまり最強!!