ポアソンの法則を断熱変化による気体分子運動論で導出してみた
どうも！オンライン物理塾長あっきーです
オンライン物理塾長あっきー
入試問題で気体分子運動論が出てくるときは、「断熱変化→ポアソンの式導出」というパターンが多いです。
ですから、一回でも触れておくと入試問題で出てきたときに安心して解けるようになります。
この記事では、断熱変化における気体分子運動論を考え、ポアソンの式を導出していきます。
入試そのまま出るような問題になっていますので、最後まで読んで流れを押さえましょう！
目次
気体分子運動論、ポアソンの式とは
気体分子運動論というのは分子の運動から気体の性質を考えることです。
また、ポアソンの式は断熱変化における圧力と体積の関係を表したものです。
これらは前提知識として理解しておくといいでしょう。詳しくは以下の記事を読んでください！
気体分子運動論によるポアソンの式導出問題
断面積\(S\),長さ\(L\)のシリンダー内の気体分子(質量\(m\))の運動を考える。ピストンは左向きに\(v_p\)の速さで動いている。また、分子の速さは\(v\)であり、各成分の速さはそれぞれ\(v_x , v_y , v_z\)である。初期状態では\(v_x = v_y =v_z\)としてよい。ただし、ピストンの速さは分子の速さより十分小さいとする。また、軸を図のように取る。
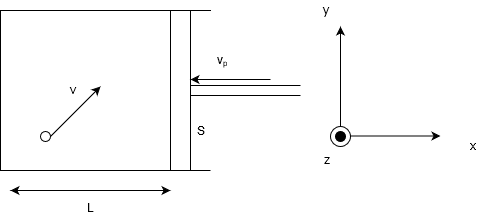
(1) 分子はピストンと弾性衝突する。一度の衝突による運動エネルギーの変化量を求めよ。ただし、\(|x| \ll 1\)のときの近似式、\(1 + x)^\alpha = 1 + \alpha x\)を用いること。
(2) ピストンが変位\(\Delta \vec{L} = (\Delta L)\)動いたときを考える。この時、ピストンの移動距離は小さいのでこれは無視してよく、分子の速さも変化しないものとみなしてよい。この間の運動エネルギーの変化量を\(\Delta L, L, m ,v_x\)を用いて表せ
(3) 分子の運動エネルギーはボルツマン定数\(k\)を、温度\(T\)[K]を用いて、\(\frac{3}{2}KT\)と表せる。これを利用し、初期の温度\(T\)を\(k , m ,v_x\)を用いて求めよ
(4) 初期状態から(2)の状態にまでについて、温度の変化量\(\Delta T\)、ピストンの移動距離\(\Delta L\)の関係を、\(T , L\)を用いて求めよ
気体分子運動論によるポアソンの式解説
ここから解説に入ります。まずは自力で解いてくださいね。
(1) 反発係数の式がしっかり使える？
衝突に関する話なので運動量や反発係数が使えますよね。ここでは反発係数を考えた方がよさそうです。
問題文に「弾性衝突する」と書いてあります。つまり、反発係数が1ですね。
反発係数は
\(e = – \frac{後の相対速さ}{前の相対速さ}\)
と書けるので、衝突後の速さ\(v_x’\)とすると次のように表せます。
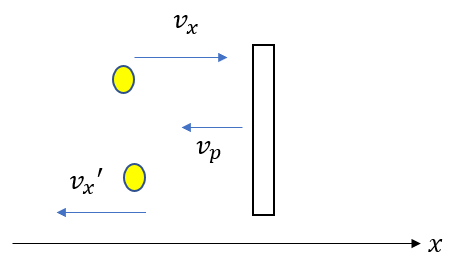
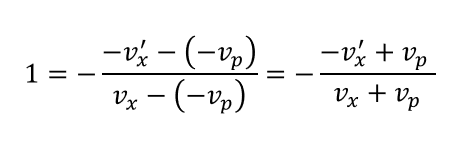
衝突後の速さが求められますね
\(v_x’ = v_x + 2v_p\)
衝突後の速さが分かれば運動量の変化量も求められます。
変化量なので「（後）－（前）」で表します。マイナスが出ようと必ず（後）－（前）です。
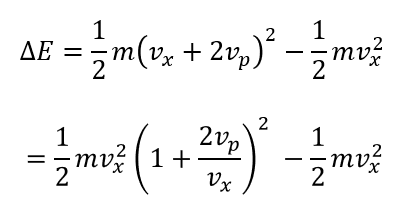
このような形にしたのは近似式を使うためです。
「\(|x| \ll 1\)のときの近似式、\(1 + x)^\alpha = 1 + \alpha x\)」
気体分子の速さ\(v_x\)はピストンの速さ\(v_p\)より十分に大きいので
\(\frac{v_p}{v_x} \ll 1\)
となります。なので近似式が使えます。
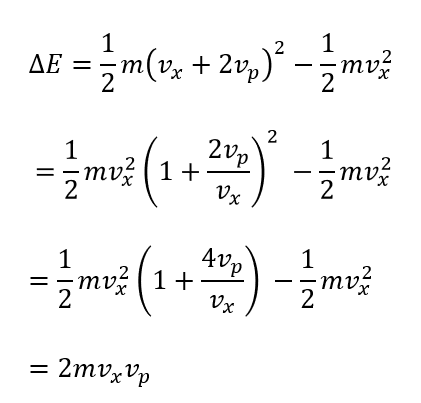
これが答えです。
(2) 微小時間の衝突回数は？
(1)では「一回の衝突でどれだけエネルギーが変化した？」ってのを求めた。ここでは、「n回の衝突でどれだけエネルギーが変化した？」っていうのを求める。
そのために、微小時間\(\Delta t\)の間にどれだけ衝突するかを求めないといけないんだ。
今回、ピストンの移動距離は無視していいので、分子は\(2L\)動いた後にまた、ピストンと衝突する。
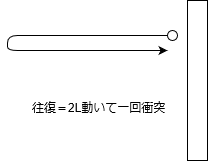
\(\Delta t\)の間に分子は\(v_x \Delta t\)だけ移動するから、衝突回数は
\(n = \frac{v_x \Delta t}{2L}\)
また、この\(\Delta t\)はピストンが\(\Delta L\)だけ移動するのに要した時間だ！！
ですが、この\(\Delta t\)を求めるのにちょっと注意が必要なんだ。
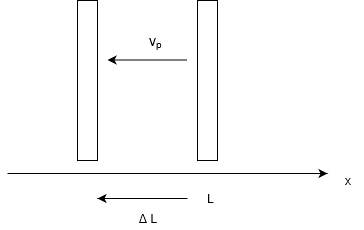今回与えられている\(\Delta \vec{L}\)ってのは変位なので、ベクトルなんですね。
\(\Delta \vec{L} = \vec{v_p}t\)より、成分を代入して
\(\Delta L = -v_p \Delta t\)
\( \Delta t = – \frac{\Delta L}{v_p}\)
「あれ、時間がマイナスになっているんじゃ・・・」
って思うかもしれないけど、あってます。
変位の成分を\(\Delta L\)っておいてますが、これって明らかに負ですよね。だから、マイナスを掛けたら正になる。
結局 \(\Delta t = – \frac{\Delta L}{v_p}\)と表せる！
ということで、一回で(1)だけエネルギーが変化するんだから、n回では？・・・
\(\Delta E = 2mv_x v_p ・\frac{v_x}{2L} = \frac{v_p\Delta t}{L}mv_x^2\)
さっきの\(\Delta t\)を代入して
\(\Delta E = -\frac{\Delta L}{L}×mv_x^2\)
ま、なんでこうもベクトルやらマイナスやらが出てくるかっていうのは、ポアソンの式というのを出すにあたって厳密な設定をしないといけないんですね。この厳密な設定ってのが軸とベクトルなんですよ。だから、面倒なのはしょうがないことなんですよね。
(3) 初期状態の運動エネルギーを二通りで表す。
ここでは初期状態の運動エネルギーについて考えている。
初期状態では各速度成分は同じなので運動エネルギーは
\(E = \frac{1}{2}mv^2 = \frac{1}{2}(v_x^2 + v_y^2 + v_z^2) = \frac{3}{2}mv_x^2\)
んで、問題文で運動エネルギー\(E\)は\(\frac{3}{2}kT\)と表せるから。これらの式を結べば
\(\frac{3}{2}kT = \frac{3}{2}mv_x^2\)
∴\(T = \frac{1}{k}mv_x^2\)
ちなみに、運動エネルギーが\(\frac{3}{2}kT\)で表せるのは気体分子運動論で扱っています。
(4) 変化量をイコールで結ぶ
(4)は今まで出したものをつなげていくだけ。
まず\(E = \frac{3}{2}kT\)から、kは定数なので、エネルギーの変化量は温度の変化量だね。
つまり
\(\Delta E = \frac{3}{2}k\Delta T\)
んで、エネルギーの変化量は(2)で
\(\Delta E = – \frac{\Delta L}{L}mv_x^2\)
と求まっているね。
なのでこれらを結べば
\(\frac{3}{2}k\Delta T – -\frac{\Delta L}{L}mv_x^2\)
また(3)より\(mv_x^2 = kT\)と表されるので
\(\frac{3}{2}k\Delta T = -\frac{\Delta L}{L}kT\)
∴\(\frac{\Delta T}{T} = -\frac{3}{2}\frac{\Delta L}{L}\)
以上ですべて答えることができましたね。
最後の関係式からポアソンの式が得られる
(4)の最後の式は、実はポアソンの式を導出してみたで出た式と同じなんですね。
物理では
「微小変化(つまり0の極限)を足していく」
という考え方をするんだ。
これって結局積分ね。
さっきの式で\(V = SL\)という関係を使うと
\(\frac{\Delta T}{T} = -\frac{3}{2}\frac{\Delta V}{V}\)
となります。
\(\Delta T , \Delta V\)を0に近づけるとそれぞれ\(dT, dV\)となる。
それを積分すると
\(\int { \frac{1}{T}dT} = -\frac{3}{2}\int {\frac{1}{V}dV}\)
これは
\(\log{T} = -\frac{3}{2}\log{V} + C\) {Cは積分定数)
となってさらに整理して
\(\log{TV^\frac{3}{2}} = 一定\)
logが一定なら、その中身も当然一定です。
\(TV^{\frac{3}{2}} = 一定\)
これがポアソンの式です。
ま、こういう微積を使うのは受験では出ないので安心してください。
積分する前までの問題は解ききってくださいね。
