力学のモーメントの問題。「倒れる」条件を徹底解説!!

モーメントの問題で「倒れる」みたいな問題があるじゃないですか?あれの解説をしてほしいです!
 AI
AI
よし、実際に演習してみよう。モーメントのポイントは「つり合い」。たったこれだけです。
 AKINORI
AKINORI
モーメントの問題では、よく「(滑らずに)倒れる」という条件を考える問題がよく出てきます。
それを詳しく考えてみましょう。
モーメントの問題で考えるべきことはたったひとつです。それは・・・
つりあい
です。
では、やっていきましょう!!
問題
粗い床上に、重さ\(W\)、高さ\(a\), 幅\(b\)の直方体が置かれている。図の点A,Bは、直方体の側面に平行で重心を通る断面の点を表す。点Aに糸を取り付け、水平右向きに大きさ\(T\)の張力で引いた。はじめ直方体は静止していたが、\(T\)を徐々に大きくすると、やがて点Bを回転軸として倒れた。次の各問に答えよ。
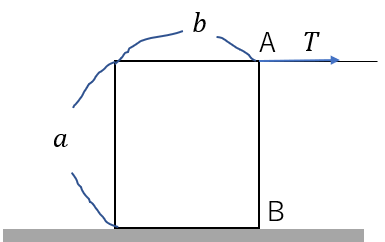
(1)直方体が静止しているとき、直方体が床から受ける垂直抗力の作用点は、点Bから左向きにいくらの距離にあるか。
(2)直方体が回転し始めるのは、\(T\)をいくら超えたときか。
(3)床と直方体の間の静止摩擦係数\(\mu\)は、いくらより大きくなければならないか。
(セミナー物理基礎・物理 2016 , 発展例題11)
(1)「静止」=「つりあい」
「静止」って書いてあるからもちろん「つり合い」を考えるんですね!!
 AI
AI
剛体のつり合いに関してはこちらをチェック↓
剛体のつり合いを考えるためには以下を考える必要がありましたね。
- 力のつり合い・・・「合力=0」
- モーメントのつり合い・・・「モーメントの和=0」
これを使うことを頭に入れておいてください。
では、まず力探しをしましょう!!
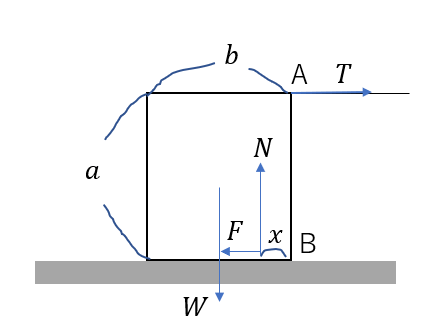
この問題でちょっと疑問に思ったんですけど、垂直抗力の位置って中心\(\frac{b}{2}\)の位置じゃないんですか?
 AI
AI
確かにそう思うよね。これは実際にモーメントのつり合い式を立ててみるとわかるよ。
 AKINORI
AKINORI
とりあえず、力のつり合いを考えます。
\(W = N\)
\(F = T\)
ですね。
そして、Bまわりのモーメントのつり合いを考えます。
反時計回りを正とするので
\(W\frac{b}{2} – Ta – Nx = 0\)
ここがAIさんの疑問ですね。
「なんで垂直抗力の位置が\(\frac{b}{2}\)の位置じゃないの??」
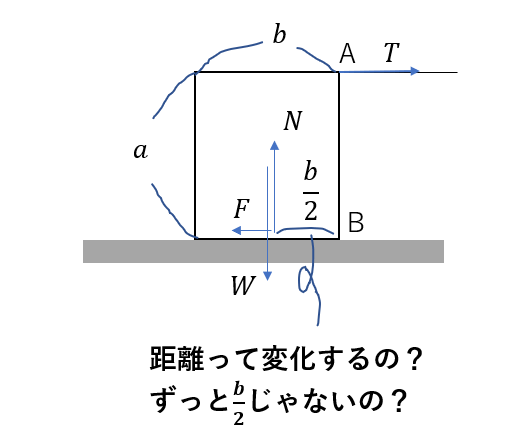
さっきの式を少し変形します
\(W\frac{b}{2} = Ta + Nx\)
この中で一定のものを見てみると・・・
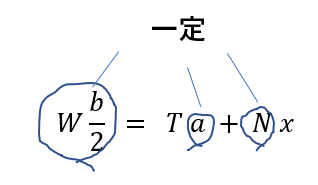
こうですね。
特に左辺が一定というのがポイントです。
今回、\(T\)を大きくしていくと、右辺が大きくなっていきますね。
でも、左辺は一定ですから、右辺が大きくなった分はどこかで打ち消さないといけません。
打ち消すには、\(x\)の値を小さくするつまり
垂直抗力の作用点をBに近づける必要がありますね。
ですから、垂直抗力の作用点は\(\frac{b}{2}\)の位置に常にあるわけじゃないんです。
なるほど!!
 AI
AI
さて、本題に戻りましょう。
もう一度、ここまで導いた式を見直しましょう
- \(F = T\)・・・①
- \(W = N\)・・・②
- \(W\frac{b}{2} – Ta – Nx = 0\)・・・③
②と③を使って\(x\)を求めればいいですね。
\(x = \frac{b}{2} – \frac{T}{W}a\)
(2)「回転し始める」=「ギリギリつり合い」
これは知っておいてほしいんだけど、「〇〇し始める」っていう言葉は「ギリギリ△△」って言い換えられます。
 AKINORI
AKINORI
どういう意味かというと、
今回は「回転し始める」って書いてありますね。ある\(T\)を境に直方体が
静止→回転
と変わる瞬間ということです。
ということは、その瞬間までは「ギリギリ静止している」と考えていいですよね。
このように
「回転し始める」→「ギリギリ静止している」
と言い換えができるってわけです。
「静止」しているわけですから、(1)がそのまま使えるわけですね。(1)は「静止」の状態を考えていたわけですから。
ギリギリ静止しているとは(1)の式で\(x = 0\)としたときですね。
\(x= 0\)を代入して、\(T\)を求めらば、それが答えです。
\(0 = \frac{b}{2} – \frac{T_1}{W} a\)
よって
\(T_1 = \frac{b}{2a}W\)
「〇〇し始める」=「ギリギリ△△」ですね。(例:「B’zを歌い始める」=「ギリギリchop」(笑))
 AI
AI
AIさん・・・
 AKINORI
AKINORI
(3)回転 or 滑る?
静止摩擦係数?そんな条件どうやって考えるんですか?
 AI
AI
今回は条件によっては回転する前に滑ることがあるんだ。
 AKINORI
AKINORI
今回、\(T\)が大きくなると回転するんですが、それと同時に静止摩擦力も大きくなっていきます。
ですから、もし回転し始める(\(x = 0\)になる)前に最大摩擦力になってしまったら、回転する前に滑ってしまいます。
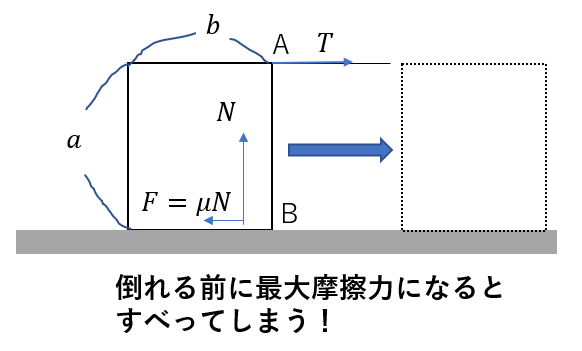
ですから、静止摩擦係数の条件を考えるってわけです。
じゃあ、条件を考えるんですが、もう答えは言っていますね。
\(x = 0\)になる前に最大摩擦力\(F = \mu N\)になったら滑っちゃうので
常に\(F \le \mu N\)
となっていればいいんですね。
\(F = T\)
\(W = N\)
なので
\(T \le \mu W\)
です。
これが常に成り立つためには
(2)で求めた\(T\)の最大\(T_1 = \frac{b}{2a}W\)
が\(\mu W\)より小さければいいんですね。
ということで
\(\frac{b}{2a}W < \mu W\)
よって
\(\mu = \frac{b}{2a}\)
これが答えです。
結局、つり合いを考えているだけなんですね。
 AI
AI
そう!あとは、「〇〇し始める」とか「摩擦力」とかの条件をその都度考えられると点数が伸びるよ!
 AKINORI
AKINORI
まとめ
- モーメントの問題・・・つり合いを考える!!
- 「〇〇し始める」=「ギリギリ△△」










Comment
わかりやすい解説をありがとうございます。
(3)の答えがμ=b/2aと表示されていますが、μ>b/2aが正しいと思います。