高校物理の位相とは?波でも交流でも意味は同じです

どうも!オンライン物理塾長あっきーです!現役で早稲田大学に合格し、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
物理で出てくる「位相」と言うのが分かるようでわかりません!分かりやすく教えてほしいです…
 リケジョになりたいAIさん
リケジョになりたいAIさん
今回はこの悩みを解決していきます。
位相って分かるようでわかりませんよね。僕も同じように思っていました。
結論から言いますと、位相とは「振動の様子」です。
はい、以上終了、閉廷!
・・・というわけにはいかないので位相について円運動や波などの具体例を出しながら、位相について見ていきましょう!
位相の正体は「振動の角度」であること
位相のずれの意味
初期位相とは?
目次
物理の位相とは「振動の様子」です
物理では位相のことを英語で “phase” と言います。ゲームでモンスターが姿形を変えて「フェーズ2」とか聞いたことあると思います。あのフェーズです。
位相とは振動の様子です。
高校物理でも4つの振動を扱います。
- 円運動
- 単振動
- 波
- 電気(交流)
振動においてはこの位相という概念を取り入れることであるメリットが出てきます。
位相を考えることで物体の振動状態が分かる
そのメリットは振動の状態が分かることです。
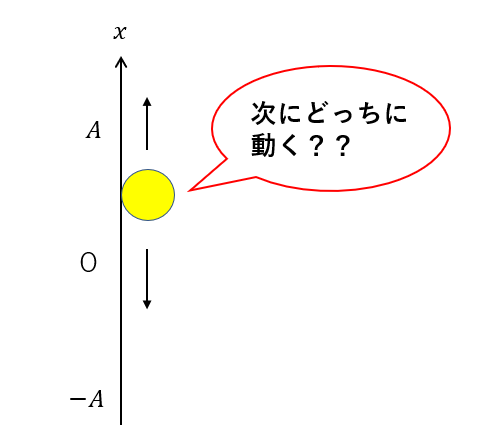
単振動する物体は同じ位置にあっても左右(上下)のどちらに動くかは図にしてしまうと分かりませんね。
それを明らかにするのが位相の役割です。
物理の位相は角度で表される「グラフ」と「式の角度」
「位相は振動の状態です」と言われても抽象的なので、もう少し詳しく見ていきます。
物理では位相は角度として表されます。(その理由は後程説明します。)
そして、2種類の場面で表されます。
位相が使われる場面
- グラフ
- 式
物理の位相1:グラフにおける角度
例えば正弦波のグラフは次のような形になりますね。
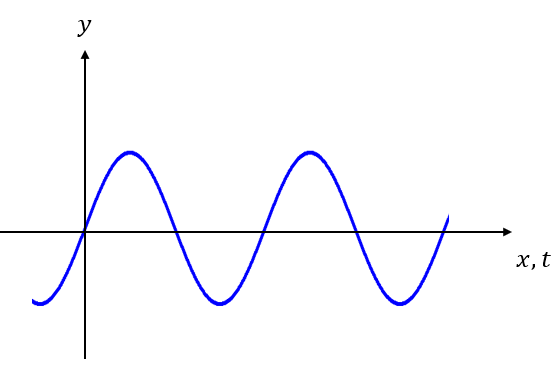
(横軸はxかtかでグラフの意味が変わるので注意)
波のグラフは波の形状(波形)やある点の振動の仕方を見ることができるんですよね。つまり
- 波の形状→各点の振動の状態が分かる
- ある点の振動の仕方→ある点の振動の状態が分かる
ということですね。これを数値に置き換えたものが位相ということです。
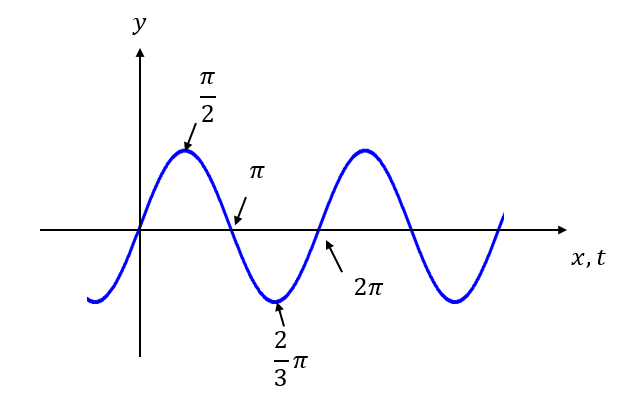
グラフを見ても分かるように、\(y=0\)となる点はいくつかありますよね。ですが、いずれも振動の状態が違うのです。
それを\(\pi\)や\(2\pi\)で表すことができ、違いを区別できるのです。
なぜ\(\pi\)などで表されるのかというのは後ほど説明しますが、このように位相をある数値として表すことで振動の状態を表すことができます。
物理の位相1:式における角度
また、正弦波の式は次のように書けます。
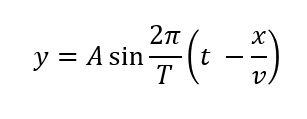
正弦波お式に限らず、振動の場合は必ずsinやcosの式で表されます。
このsinとcosの中身は角度が入りますよね?
そして先ほども言ったように位相は角度で表されます。
つまり、このsinやcosの中身こそがまさに位相を表しているのです。
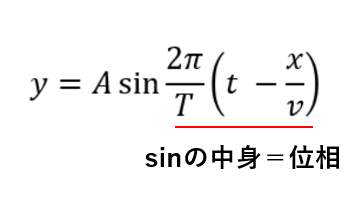
このように、グラフと式で位相が見られます。
物理の位相の具体例
ではこれを踏まえて、高校物理で出てくる4つの振動の中で位相を見ていきましょう。
円運動の位相
円運動が位相の根源となります。
円運動では角速度\(\omega\)、時間\(t\)を使って物体の角度を表すことができます。
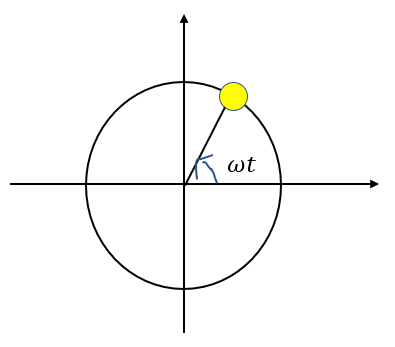
円運動も同じ運動を続けるので振動と同じです。
ですから、この\(\omega t\)という角度が振動の状態(物体の位置)を表す位相となるのです。
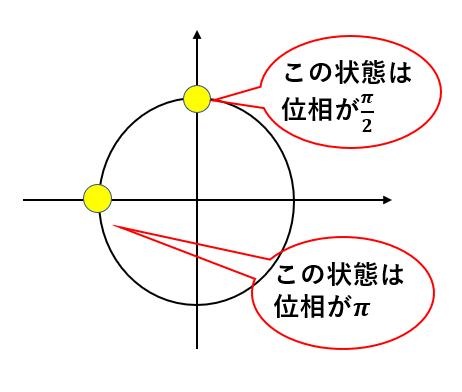
最初に「位相は角度で表される」と言ったのは位相が円運動から来ているからなんです。
そして、角度ということなので弧度法を使って\(\pi\)などで位相を表すことができるのです。
円運動に関してはこちらの記事で説明しています。
単振動の位相
単振動は円運動を1つの方向だけで見た場合の運動でした。
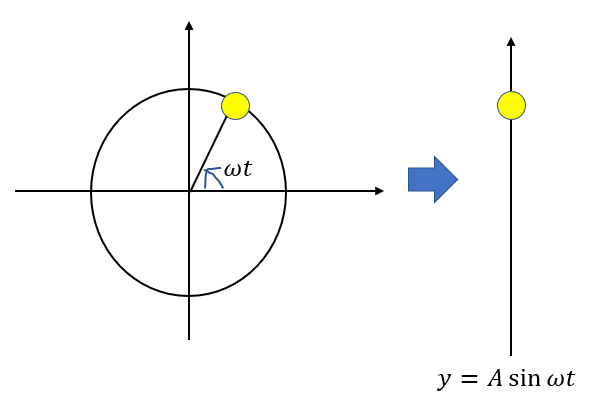
円運動は平面の運動なわけですが、それを直線の運動に見たわけです。
そのため、単振動は同じ位置でも上に動くか下に動くか分からないという状況が起こります。
しかし、もともと円運動だったわけなので、円運動に戻してあげれば振動の状態が分かります。
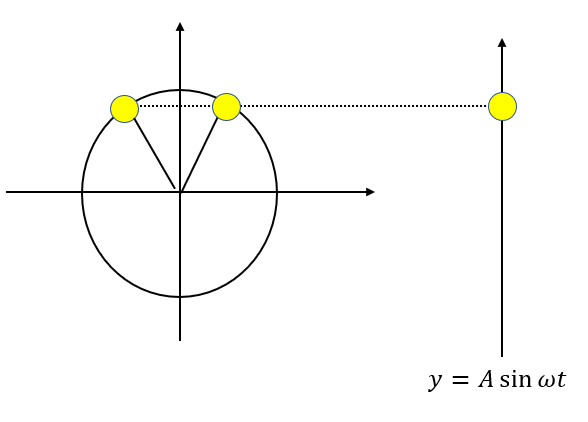
単振動に限らずですが、振動を表すものはすべて円運動に置き換えることで位相が分かりやすくなります。
単振動についてはこちらの記事をご覧くださいね。
波、交流回路の位相
波でも交流回路でも考え方は同じです。
しかし、波や交流回路では位相のずれというのがありますよね。
光の反射の際に「位相が\(\pi\)ずれる」というのがあったり
交流回路のコイルでは「電流が電圧より\(\frac{\pi}{2}\)遅れる」とかありますよね。
この意味もここまでの内容が分かっていれば説明できます。
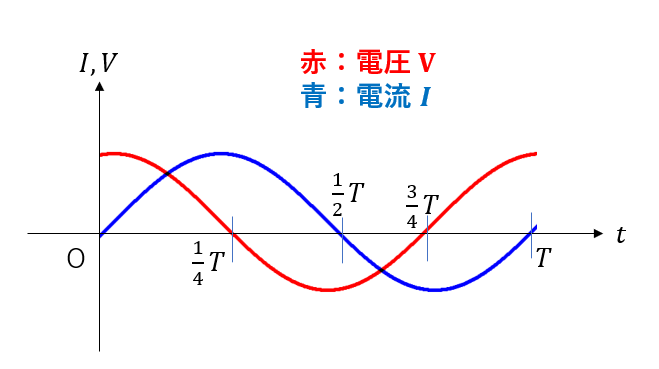
これはコイルに関する電圧と電流の時間変化をグラフにしています。
コイルは「電流が電圧より\(\frac{\pi}{2}\)遅れる」でした。
つまり、例えば\(t=0\)のときに\(I=0\)だとしたら、電圧は\(\frac{\pi}{2}\)だけ進んだ位置、つまり最大値を取ることになります。
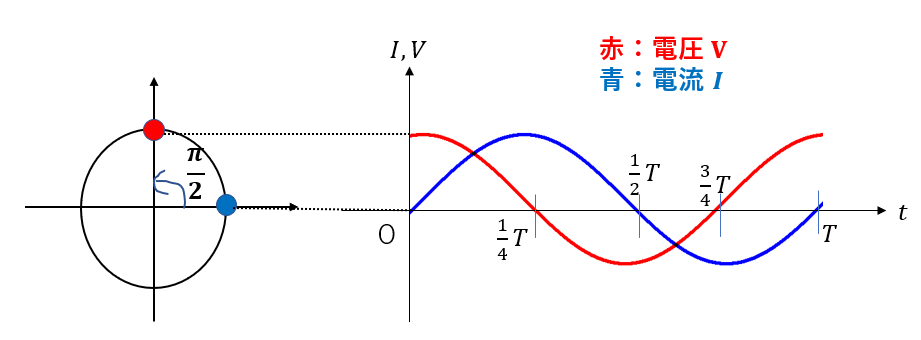
コンデンサーの場合も、また光の位相のずれも全く同じように考えることができます。
波や交流回路に関しては以下にまとめていますのでご覧くださいね。
初期位相とは?
物理でたまに初期位相という言葉を聞きますね。これも位相の概念が分かれば簡単です。
例えば単振動の位置の式は次のように表せます。
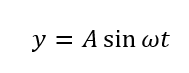
しかし、これは\(t=0\)のときに\(y=0\)となる場合を表しています。
もしかしたら、\(t=0\)のときに\(y=A\)かもしれませんよね。
その時に登場するのが初期位相です。
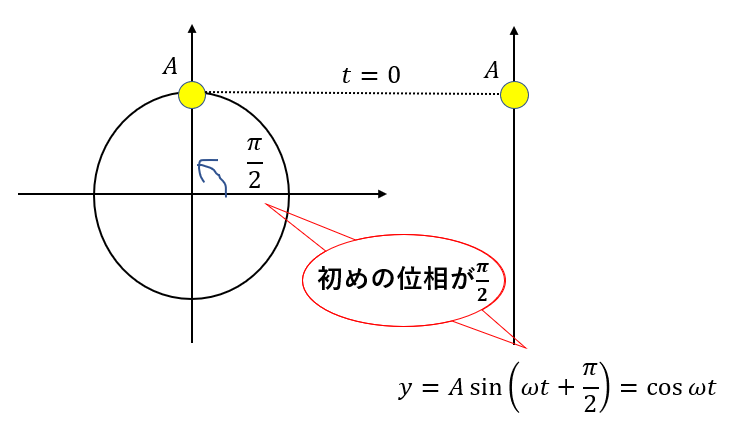
このように単振動で\(t=0\)のときに\(y=A\)となるということは、円運動においててっぺんにあるということですよね。
なのでsinの中身に\(\frac{\pi}{2}\)を足してあげる必要があるのです。この\(\frac{\pi}{2}\)が初期位相です。
ちなみにこれを計算すると\(\cos{\omega t}\)になります。
sinかcosかの違いは位相の違いでしかないということですね。
まとめ:位相とは振動の状態を表す角度
いかがでしたか?
位相について細かく問われる入試問題はまずありません。
しかし、用語として理解しておかないと、交流回路などで混乱するのでここでバッチリ理解しておきましょう!
位相とは
→振動の状態を表す角度