ポアソンの式とは?断熱変化で微小変化を扱い導出する方法

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
熱力学の断熱変化のところでポアソンの式というのを習いましたか?
ポアソンの式は覚えてなくても問題文で与えられることが多いです。
でも実は、入試ではポアソンの式を使うよりポアソンの式を導出する問題の方が多いです。
導出は難しくなく、断熱変化と微小変化の扱いが分かっていれば簡単に導くことができます。
この記事では、ポアソンの式の導出をわかりやすく解説していきます。
一度触れておけば、入試でポアソンの式の問題が出ても焦らず取り組めるので最後まで読んでくださいね。
目次
ポアソンの式の導出で大事なこと

ポアソンの式の導出をしていくのですが、先にポイントだけ説明していきます。
ポアソンの式は断熱変化で成り立つ圧力と体積の関係式のことです。
そして、これは熱力学のお話です。
熱力学と言えばパッと浮かばなきゃいけない式が2つありましたね。
- 状態方程式
- 第一法則
この二つです。
断熱変化でこの2大公式をうまく使うことがカギです。
・・・え?2大公式が分からない?
その場合はこちらをチェックしましょう!
【物理】気体の状態方程式の意味と使い方。ボイルの法則?そんなのいらないよ
ポアソンの式導出:微小変化を考える

まず、はじめに圧力、体積、温度、物質量がそれぞれ\(P,V,T,n\)の単原子分子理想気体を考えます。
ここから、断熱変化によって\(\Delta P, \Delta V, \Delta T\)だけそれぞれの微小変化した場合を考えましょう。
微小変化した後で状態方程式が立てます。
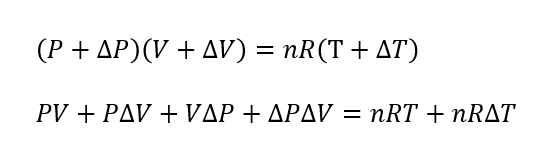
また、変化前でももちろん状態方程式は立てられるます。
\(PV = nRT\)
この2式から次のように整理できます。

さて、今は微小変化を考えています。つまり\(\Delta P, \Delta V, \Delta T\)は非常に小さい値です。
特に\(\Delta P \Delta V\)は「(極小)×(極小)」ですから、超スーパー小さい値なわけです。
なので、これは無視してOKです。
ということで、式を整理します。
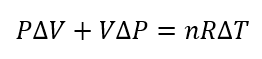
ちなみに、この微小量の扱い方には慣れておいた方が良いです。
特に微小量同士の掛け算(2次の微小量)や\((1 + x)^n\)の近似式は知っておくと便利です。
もちろん入試では説明が載っていますが、知っておいて損はありません。
ポアソンの式導出:熱力学第一法則を使う

状態方程式を使ったのでもう2大公式のもう一方である熱力学第一法則を使いましょう。
第一法則はお金の関係でした。
\(Q = \Delta U + W\)
お金\((Q)\)をもらったら貯金(\(\Delta U\))するか、使うか\((W)\)という関係でしたね。
今回は断熱変化なので、\(Q = 0\)です。
また単原子分子理想気体ならば内部エネルギーに関して
\(\Delta U = \frac{3}{2}nR\Delta T\)
と書くことができます。
そして、微小変化なので\(P\)の変化はない、つまり\(P\)は一定と考えます。
すると仕事に関して
\(W = P\Delta V\)
と書くことができますね。
まとめると以下のように表せます。
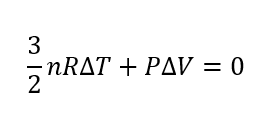
ポアソンの式導出:PとVの関係に持ち込む

ここから\(P\)と\(V\)の関係にもっていきます。
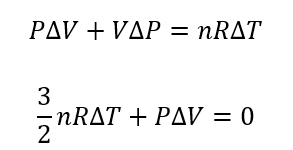
先ほど求めたこの2式から\(\Delta T\)を消去しましょう。
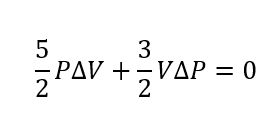
ここで少し式変形します。

しつこいですが今は微小変化を考えていて、\(\Delta P, \Delta V\)は本来0に近づける必要があります。
この時、左辺の\(\frac{\Delta P}{\Delta V}\)の部分は微分記号に置き換わります。
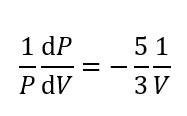
これは微分方程式と言われるものです。高校生は必修分野ではないので解けなくても大丈夫です。
なので、ここまで理解できていればOKです。
一応計算過程もお見せします。
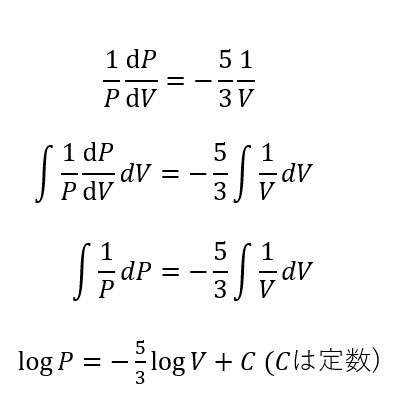
このように解くことができます。
これをもう少し変形します。

この最後に出た式がポアソンの式と呼ばれているものです。
T,Vの関係で表すと?

これは別の表現方法として、\(T, V\)で表すこともできます。
\(PV = nRT\)を使って\(P\)を消去すると・・・

このように表すこともできます。
ポアソンの式の特徴
ポアソンの式が導出できたので、このポアソンの式の特徴について2つ解説したいと思います。
\(\gamma\)は比熱比を表す。
ポアソンの式で\(\gamma = \frac{5}{3}\)と置きました。
これは実はただの定数ではなく、意味を持った値です。
\(\gamma\)を次のように見てみます。
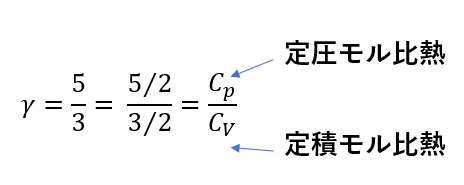
あえて、分母分子に\(\frac{1}{2}\)を掛けると、モル比熱を使って置き換えることができるのです。
モル比熱の比になっているので\(\gamma\)は比熱比と呼ばれています。
これは単原子分子に限らず、二原子分子、多原子分子でも\(\gamma = \frac{C_p}{C_V}\)で表せます。
単原子分子では\(\frac{5}{3} = 1.666\)、二原子分子では\(\frac{7}{5} = 1.4\)となります。
そしてこの比熱比は大きいほど温度上昇しやすいです。
つまり、二原子分子よりも単原子分子の方が温度が上がりやすいということになります。
等温曲線と断熱曲線の違い
教科書や問題集で「断熱曲線の方が等温曲線よりも急」というのを習ったかと思います。
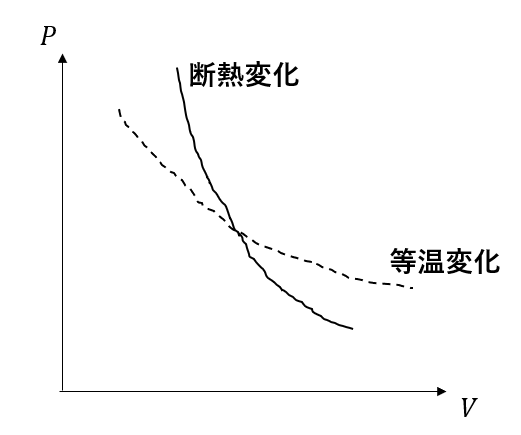
このように、\(P,V\)のグラフをみると断熱変化の方が急になっていることが分かります。
等温変化の場合は\(PV = nRT\)より
\(P = k_1 V^{-1}\)と表せます。
一方で断熱変化では先ほどのポアソンの式から
\(P = k_2 V{-\gamma}\)と表せます。
\(\gamma\)は1より大きい値ですから、断熱変化の方が急激に変化することが分かりますね。
ま、微分方程式が入っているので受験には出ません。多くの場合ポアソンの式は問題文んい書かれているので安心して大丈夫です。
まとめ:ポアソンの式は断熱+微小変化

いかがでしたか?
ポアソンの式そものもは大事ですが、その導出の流れもまた大事です。
これは、2大公式と断熱変化というところを意識しただけです。
つまり、熱力学の問題の解き方をそのまま適用しているだけなんです。
なのでポアソンの式を導出できるということは、熱力学の問題が解けるレベルに達しているということになるので、一度式を自分で導出してみましょう。








