万有引力の位置エネルギーにマイナスがつく理由を分かりやすく解説

こんにちは!ネット上で物理塾を運営しているあっきーです
 あっきー
あっきー
・万有引力で位置エネルギーの導出方法がわからない
・万有引力の位置エネルギーでマイナスがつく理由が分からない
・なんで電位はマイナスつかないで万有引力はつくのか分からない
・重力の位置エネルギー\(mgh\)と何が違うのか分からない
 リケジョになりたいAIさん
リケジョになりたいAIさん
このような悩みを持っていませんか?
実は万有引力の位置エネルギーにマイナスが付くのは当たり前のことなのです。
なぜなら、万有引力の位置エネルギーを導出した結果、そうなっただけの話だからです。
高校生では微分積分を物理を使わないので万有引力の位置エネルギーの導出は詳しくやりませんね。
\(U = -\frac{GMm}{r}\)
このような結果だけを覚えさせられて、「マイナスが付くので注意しましょう」なんていわれても
ぽか~~んとなるだけです。
今回の記事では、教科書や授業で教えてくれなかった導出を実際にしてみて、なんでマイナスが付くのかを教えていきます。
これを読むことで、万有引力の位置エネルギーについて理解が深まるとともに、万有引力の問題もすらすら解くことができます!
目次
万有引力とは?

まず万有引力というものが何か?ここから確認しましょう!!
太陽の周りを地球が回りますよね。あれは円運動です(正確には円運動ではありませんが)。
円運動の場合は中心向きに力が働いているのでしたね。
宇宙空間には何も力が働いていないように思えますが、惑星同士が引き合う力が働いているのです。
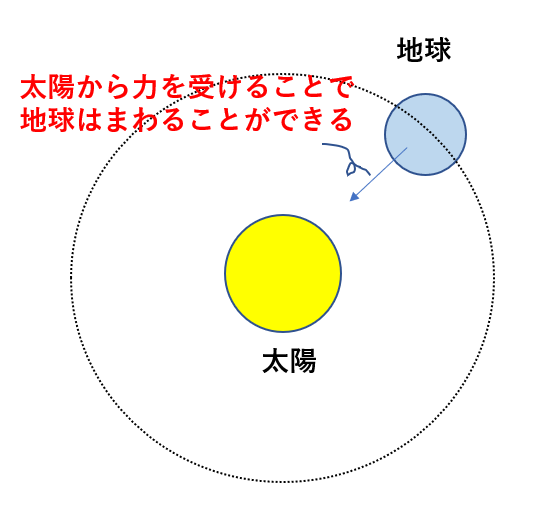
このように、質量をもつ物体同士が引き合う力を万有引力と言います。
万有引力
質量\(M,m\)の2物体が距離\(r\)だけ離れているとき、2物体にはたらく万有引力について
大きさ:\(F = G\frac{Mm}{r^2}\)
向き:引き合う向き
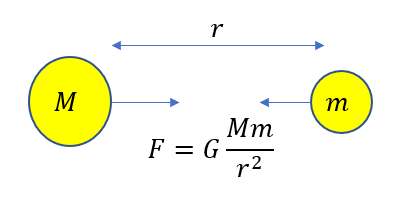
見てわかるように、質量を持つ物体同士は常に引力が働きます。
なので、人間同士も、地球上にあるすべてのものは互いに引き合っています。
・・・が、その大きさは微々たるもので、惑星レベルにならないと力を感じることはできません。
万有引力は静電気力と非常に似たような式の形をしていますね。関連付けて覚えるといいでしょう。
一つ違う点は、静電気力は電荷のプラスマイナスによって引き合ったり反発したりしますが、万有引力は質量にプラスマイナスはないため、常に引き合います。
これがのちの位置エネルギーがマイナスになる理由に大きくかかわってくるので覚えておいてください。

万有引力の位置エネルギーを求めよう

この万有引力は保存力と呼ばれるものです。保存力には位置エネルギーというものを持っています。そこで、
万有引力の位置エネルギーを求めてみましょう!!
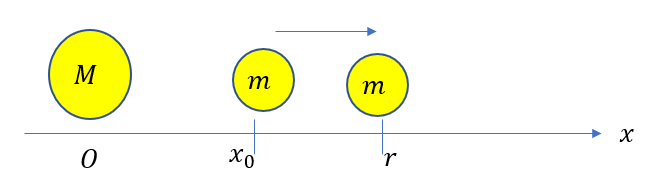
質量\(m\)の物体について考えます。
はじめ\(x_0\)の位置に静止しているところから位置\(r\)までした仕事を\(W\)としたとき、
エネルギー保存則より
(はじめの運動エネルギー)+(された仕事)=(あとの運動エネルギー)
ですから、
\(0 + W = \frac{1}{2}mv^2\)
右辺は運動エネルギーです。
つまり、この万有引力にされた仕事\(W\)はエネルギーであってほしいんです。
なのでこの\(W\)が位置エネルギーというエネルギーの一種にみなして良いことになります。
万有引力の仕事は積分で求められる

ただ、この仕事、簡単に求めることができません。
万有引力の式を見てください。位置によって大きさが変わってしまいますよね?
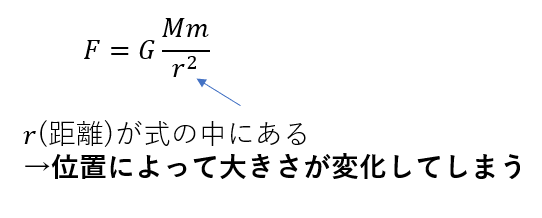
ですから、単純に「力×距離」と表すことができないんですよ。
そこで、よく使う技がこれですね。
微小変化を考える!
微小変化の詳しい話はこちら!
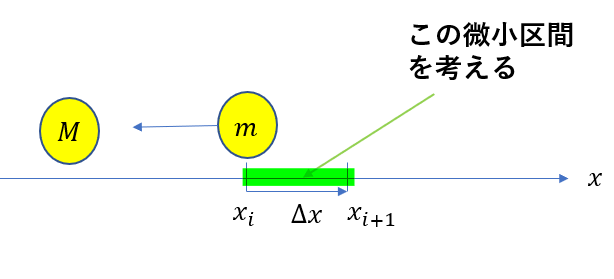
こんな感じで微小変化を考えると、距離の変化がほとんどないので万有引力は一定とみなせます。
つまり、この区間に関して言えば「力×距離」として良いのです。
\(\Delta W = \frac{GMm}{x_i^2}\Delta x\)
万有引力は左向きに対し、物体は右向きに動くので仕事は負になります。
これをグラフにすると次のようになります。
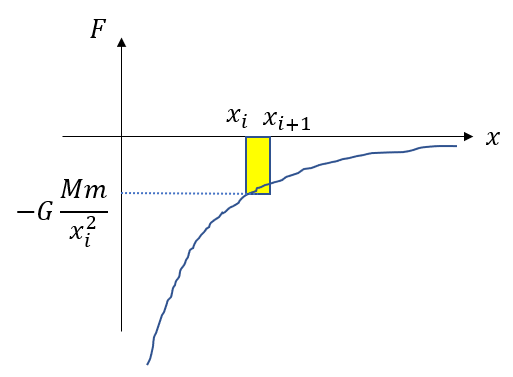
長方形の面積がまさにこの微小区間での万有引力にされた仕事になります。
そして、この長方形を\(\infty\)から\(r\)まで積み重ねていって、ぎゅっと長方形を狭めていくと・・・
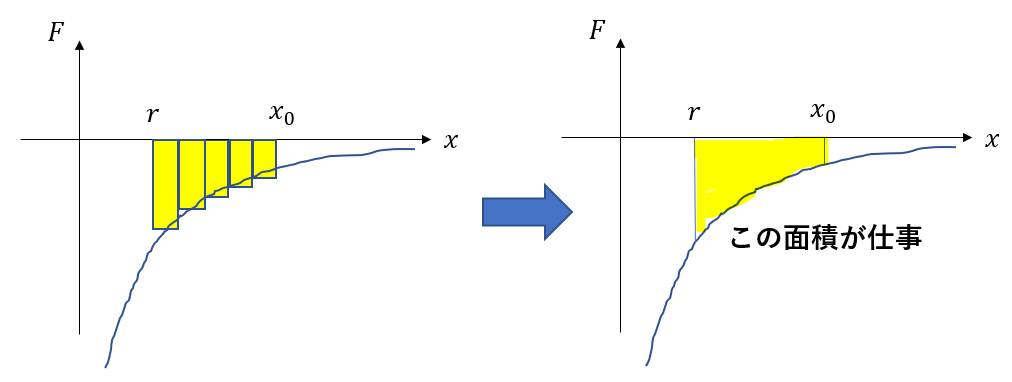
まさに積分になるわけです。
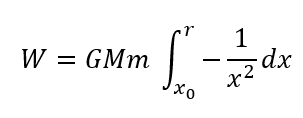
これは、高校3年生なら計算できますよね?
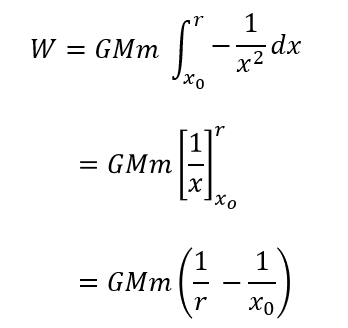
位置エネルギーには特殊な性質がある

これが位置エネルギーとなるわけですが、少し補足をしていきます。
保存力にはある特殊な性質があるのは知っていますね?
保存力にされた仕事は、経路に依らず最初の位置と最後の位置で定まるのです。
位置によって決められるから「位置エネルギー」というのが定められるのですね。
これを踏まえて、次のことが言えます。
保存力にされた仕事\(W\)は、はじめの位置エネルギー\(U_1\)とあとの位置エネルギー\(U_2\)を用いて次のように表せる
\(W = -U_2 + U_1\)
*「後-前」じゃないよ!
これは、「こう定めましょう」と決めたものなんで「なんで?」と考えず定義として覚えてください。
この\(U_1\)というのがはじめの位置エネルギーなので「基準」となるわけです。この\(U_1\)が0となるようなところを基準点に取れば、一般的な位置エネルギーを導くことができます。

位置エネルギーが0となるというのは、力の大きさが0になるということです。
万有引力による位置エネルギーでマイナスがつく理由

というわけで、\(W = -U_2 + U_1\)より
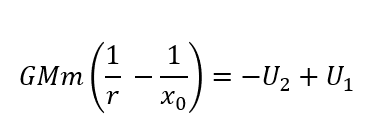
このように表すことができます。
基準点\(x_0\)をどの位置に取れば\(U_1 = 0\)になるか考えましょう。
簡単ですね。\(x_0 \to \infty\)に吹っ飛ばせば良いのです。

これが距離\(r\)における万有引力による位置エネルギーとなります。ちなみに、無限に遠く離れた場所にした点を無限遠と言います。
万有引力による位置エネルギー
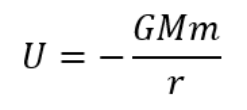
*無限遠を基準
あくまでこれは無限遠を基準にしているところに注意してください。
このように、定義にしたがって解いていったらたまたまマイナスが出てきたわけです。
導出することによって疑問が解決することもよくありますね。
重力の位置エネルギーと何が違うの?

位置エネルギーの中で重力による位置エネルギーをやりましたね。
\(U = mgh\)
で表さます。
重力は万有引力の一つなので、本質的には同じなのに式がだいぶ異なっていますね。
ですが、これもしっかりリンクしています。
実は、万有引力において知っておいてほしい関係式があります。それが
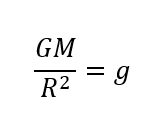
この関係です。
\(R\)は地球の半径
\(M\)は地球の質量
\(g\)は重力加速度
です。
これについて詳しい説明はこちらの記事をご覧ください。
これを使うことで、万有引力の位置エネルギーから重力の位置エネルギーを導けます。
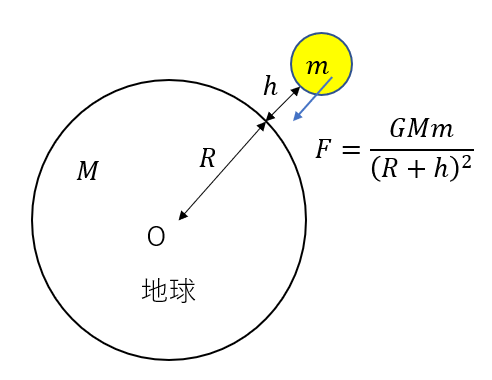
地球から高さ\(h\)の位置にある物体の万有引力の位置エネルギーは
\(U = -\frac{GMm}{(R + h)}\)
ですね。
そして先ほどの関係式を使えば次のように式変形できます。
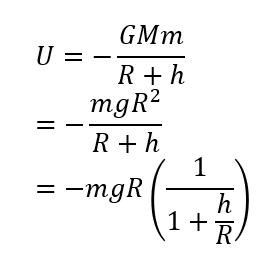
そもそも重力というは「地球表面付近での万有引力」です。表面付近ということは\(h\)は\(R\)に比べてものすごい小さい値なんですね。
なので式にある\(\frac{h}{R}\)は1よりも限りなく小さい値になります。
さてさて、ここで物理お得意の近似を使います。
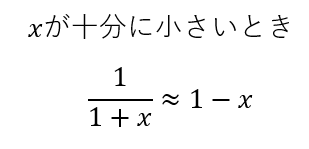
これを使ってさらに式変形すると・・・
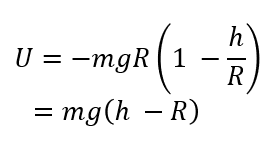
重力では地面を位置エネルギーの基準にすることが多いですね。
つまり位置\(R\)での位置エネルギー\(mgR\)を0とみなせば
\(U = mgh\)
となり、見事に重力による位置エネルギーが出ました。
なので、本質的に同じしきだったということです。
電位ではなぜマイナスがつかないの?

万有引力の位置エネルギーですが、電位もほとんど同じような式の形をしています。
\(U = \frac{kQ}{r}\)
ですが、これにはマイナスがついていませんね。
これは、電位は「+1[C]の電荷が\(+Q\)[C]の電荷による静電気力にされた仕事」から来ています。
つまり、反発し合う力が働くわけです。
万有引力とは真逆になるので、符号も逆転するのです。
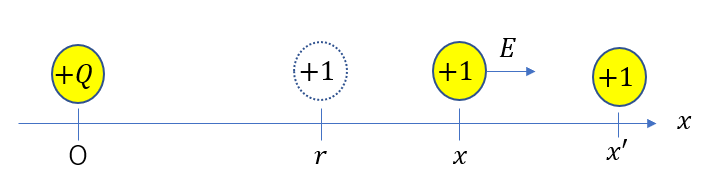
こんな感じですね。
この電位の式の\(Q\)はプラスマイナスを考慮します。なので\(-Q\)と置き換えれば、引力が働くので
万有引力と同じ形になりますね。
電位についてはこちらをチェックしてくださいね。
万有引力による位置エネルギーは何で使う?

この万有引力の位置エネルギーですが、
結局のところ重力のときの延長です。
ですから、今までやってきたエネルギー保存則で力を発揮します。
その中でも有名どころとして、
第一宇宙速度と第二宇宙速度を演習を兼ねて下の記事で押さえておきましょう。
まとめ:導出することで理解が深まる

いかがでしたか?
疑問に思っていたことは、1からやり直すことで解決することがよくあります。
僕に質問にくる人が多くいますが、たいてい「そもそも論」が抜け落ちていることが多いです。
一度戻って考えることが勉強において大事なことです。
万有引力の位置エネルギー
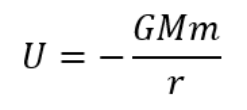
*無限遠を基準
導出をすることで、マイナスがつく理由がよくわかる!










