熱力学第一法則の問題での使い方講座。変化ごとでまとめちゃった

熱力学第一法則の問題での使い方が分かる
定積・定圧・等温変化での特徴が分かる
状態方程式は3ステップで使えばいいのはわかります。なら、第一法則も使い方のコツがあるんですか?
 AI
AI
もちろん!!状態方程式と同じように「一定」を探すことが重要!!
 AKINORI
AKINORI
状態方程式を使うときは、「絶対これでやってね!」っていう3ステップがありました。
それについてはこちらで!
熱力学第一法則も実は全く同じ重要ポイントがあってそれがそのまま熱力学第一法則を問題で使う方法になります。
それは「一定」を探すこと
熱力学全般で言えることですが、問題を解く必勝パターンは
図を書いて「一定」を探せば後は公式を適用する
たったこれだけなんです。
今回は熱力学第一法則を問題でのどのように使えるか?という使い方の部分と
その中で出てくる定圧・定積・等温変化のそれぞれの特徴を
分かりやすく説明していきます!!
↓まずは熱力学第一法則について理解しましょう!↓
熱力学第一法則とは?
熱力学第一法則とはこうでしたね。
- 熱力学第一法則
\(Q = \Delta U + W\)
「もらったお金\((Q)\)を貯金するか\((\Delta U)\)使うか\((W)\)」
・\(W = P\Delta V\)(P=一定)
・\(U = \frac{3}{2}nRT\) \((\Delta U = \frac{3}{2}nR\Delta T)\)
*注意
\(Q\):もらった熱量 → 失ったらマイナスにする
\(\Delta U\):内部エネルギーの変化量 → 絶対「後-前」なのでマイナスのこともある
\(W\):気体がした仕事 → されたらマイナス
お金の関係でしたね。
そして、今回4つ一定の場合を考えます
- 圧力
- 体積
- 温度
- 熱(断熱)
熱だけは一定というか、断熱\(Q = 0\)の場合を考えます。
では一個ずつ見てみましょう。

体積一定・・・「すべて貯金する安全型」
まずは体積Vが一定の変化(定積変化)を考えます。
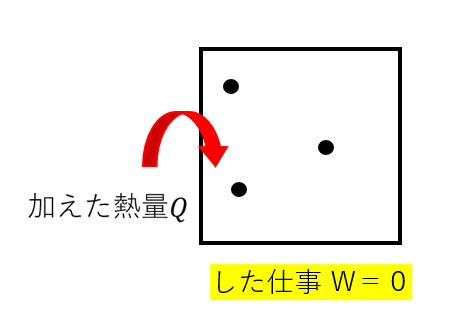
体積が一定だと何が言えるんでしょうか?
えっと・・・「移動体積」が無いからした仕事\(W = 0\)じゃないですか?
 AI
AI
その通り!
 AKINORI
AKINORI
仕事はP-Vグラフの面積で求められるんでしたよね。
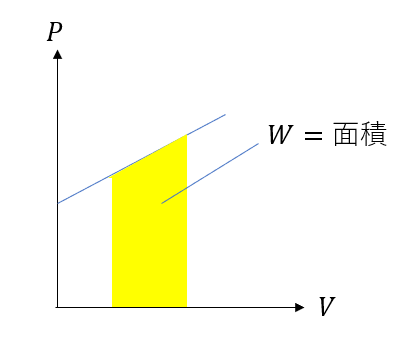
だから体積が変化しなかったら面積は0です。
なので仕事もしません。
ということで熱力学第一法則をに当てはめると
\(Q = \Delta U\)
つまり「もらったお金をすべて貯金する安全型」なんですね。
また単原子分子理想気体なら
\(\Delta U = \frac{3}{2}nR\Delta T\)
と表せたので
\(Q = \frac{3}{2}nR\Delta T\)
と書けますね。
あれ?\(nR\Delta T\)って状態方程式を使えば\(P, V\)で表せるんじゃないんですか?
 AI
AI
お!いいところに気が付いたね!
 AKINORI
AKINORI
状態方程式を見てみると
\(PV = nRT\)
ですよね。
これの変化量を考えてみましょう。
右辺が変化するとしたら\(T\)だけですね。
\(T\)の変化量を\(\Delta T\)としましょう。
さて、右辺が変化したとき、左辺は何が変化するでしょうか??
今は\(V = 一定\)だから変化する可能性があるのは\(P\)だけですね。
 AI
AI
そうだね!
 AKINORI
AKINORI
なので、\(P\)が\(\Delta P\)だけ変化すると考えれば
\(\Delta P ・V = nR\Delta T\)
という関係が成り立ちますね。
これを使えば
\(Q = \frac{3}{2}V\Delta P\)
とも表せます。
自分で「体積一定」という条件からここまで導けるようにしてください。
この考え方がそのまま問題で使えます!!

圧力一定・・・「貯金するし使う一般型」
今度は圧力が一定の変化(定圧変化)を考えますよ。
定圧変化だったら何が言えるんでしょうか??
え・・・あ!定圧だからした仕事が\(W = P\Delta V\)と書ける!!
 AI
AI
いいね!!その通り。
 AKINORI
AKINORI
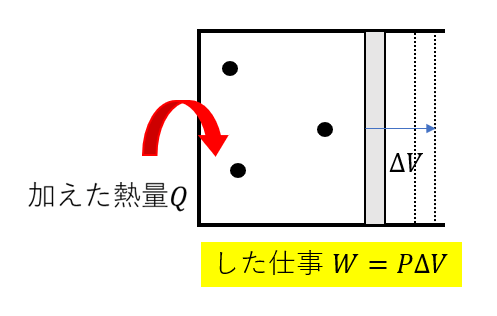
今回、\(\Delta U , W\)はともに0ではないんですが、定圧(\(P = 一定\))という条件があるから、
\(W = P\Delta V\)
と書けますね。
なので、熱力学第一法則を適用すれば
\(Q = \Delta U + W\)
\(= \frac{3}{2}nR\Delta T + P\Delta V\)
「もらったお金は貯金したり使ったりする一般型」ということですね。
そして、さっきと同様。状態方程式を考えましょう。
\(\Delta T\)だけ変化したら、今度は圧力は変化できないから\(V\)だけ変化するんですね!!
 AI
AI
そういうこと!
 AKINORI
AKINORI
\(PV = nRT\)
から\(\Delta T\)が変化すると
左辺は\(P = 一定\)なので、変化するとしたら\(V\)だけです。
なので、\(\Delta V\)という変化量だけを考えれば良くて
\(P\Delta V = nR\Delta T\)
と書けるわけです。
これをさっきの式に当てはめれば
\(Q = \frac{3}{2}nR\Delta T + nR\Delta T\)
∴\(Q = \frac{5}{2}nR\Delta T = \frac{5}{2}P\Delta V\)
と表させるわけです。
何度も言いますが、
「圧力一定」という条件からここまで導けるようにしてください。

ここまでの話からモル比熱の話につながります。
それについてはこちらから↓
温度一定・・・「すべて使う豪快型」
今度は温度一定の変化(等温変化)を考えます。
(これは定温変化とは言わないんですね(笑)。)
温度一定という条件からわかることは・・・
簡単です。\(\Delta U = 0\)ですね!!(ドヤ!!)
 AI
AI
うん・・正解だよ。
 AKINORI
AKINORI
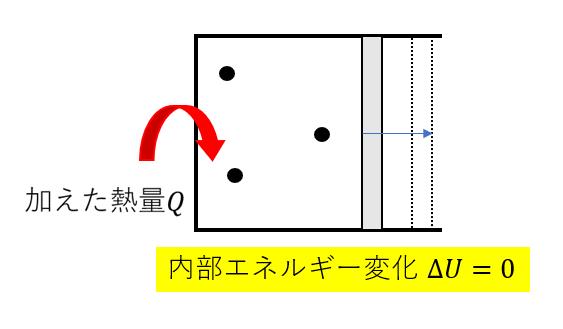
\(\Delta U = \frac{3}{2}nR\Delta T\)
と表せていたわけですが、温度一定だと当然変化量\(\Delta T\)は0ですよね。
なので\(\Delta U = 0\)です。
あとは熱力学第一法則を適用すると
\(Q = W\)
「もらったお金はすべて使う豪快型」ってわけですね。
いつも通り、状態方程式を考えよう・・・
と言っても今回はあまり、進展することは無いです。
\(PV = nRT\)
を考えると右辺は一定なので
\(PV = 一定\)
となります。
つまり、
「PとVは反比例する」
わけです。
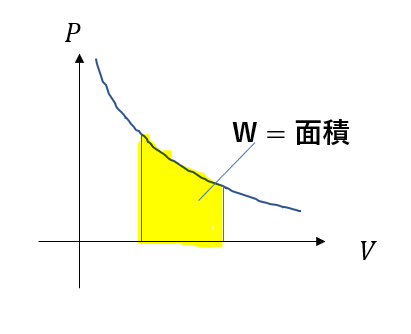
そして、このグラフの面積がまさに仕事になる。
のですが、普通は積分しないと求められません。
ということで、\(Q = W\)の式を導いた後は特にやることは無いです。
何度もいいますが、「温度一定」からここまで導けるようにしてくださいね!!
 AI
AI
あ、言われちゃった(笑)。その通りだよ
 AKINORI
AKINORI

熱量が0の場合
最後は、一定というわけではないんですが、
熱量\(Q = 0\)であるような変化(断熱変化)を考えます。
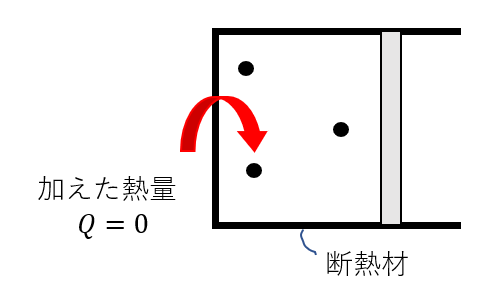
よくあるのが「断熱材でできた容器」という文言。
これは「\(Q = 0\)」っていう条件を表します。
もちろん熱力学第一法則を見てみると
\(0 = \Delta U + W\)
\(\Delta U = -W\)
さて、この式から何が言えるでしょう??
えっと。仕事をしたらエネルギーが減って、仕事をされたらエネルギーが増える?
 AI
AI
まあ、だいたいはOK。温度について詳しく見てみよう。
 AKINORI
AKINORI
この\(W\)は
気体がした仕事
ですね。
- 気体が仕事をした場合
\(W > 0\)つまり\(-W < 0\)なので
\(\Delta U < 0\)ですね。
\(\Delta U = \frac{3}{2}nR\Delta T\)ということなので、
\(\Delta T < 0\)
つまり、温度が低くなる
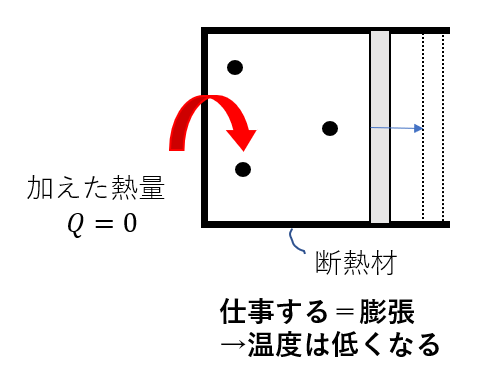
要は、空気が膨張するわけだから温度低くなる。
だから、この結果は理解できますね。
- 仕事をされる場合
これはさっきの逆を考えれば良くて
\(\Delta U > 0\)だから
\(\Delta T > 0\)
つまり、温度が高くなる
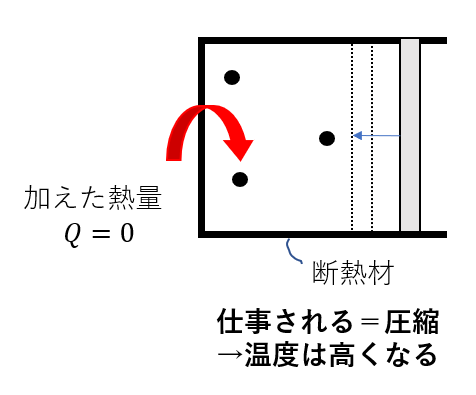
これも圧縮しているから、温度が高くなることもイメージつくね。
まとめ
特にまとめることもないんですが、一応簡単に。
「〇〇一定」という条件から
\(Q = \Delta U + W\)をうまく変形せよ!!
(まとめになってないけど・・・)
↓これもチェックしよう!↓







Comment
定期テストが近いのに全然理解出来なくて困っていました。でもこのサイトを見てすごく理解できました。本当にありがとうございます。
断熱変化は熱の出入りがないのに温度変化があってそれが今までうまく理解できてなかった。
気体が仕事をするから、その分だけ、内部エネルギーは減って、温度が低下する。
温度と熱量は同じだと思っちゃだめで、別々に考えなきゃいけない。
断熱変化と等温変化のグラフの関係がやっとわかりました。
そうですね。温度と熱量を同じものだと勘違いする人が多いので、素晴らしい発見ができて良かったです!