【物理】正弦波の式に覚え方はなかった!?導出方法を解説!
正弦波の式の導出方法が分かる
正弦波の式の使い方が分かる
初期位相について理解が深まる
こんにちは!オンライン塾を運営している、あっきーです
 あっきー
あっきー
正弦波の式が覚えられない
正弦波の式をどのように使えば分からない
 リケジョになりたいAIさん
リケジョになりたいAIさん
このような悩みはありませんか?
実は、正弦波の式は覚える必要はありません!正弦波の式は簡単に導出することができるからです。
この記事では、正弦波の式の導出方法とその意味・使い方を教えていきます。
これを最後まで読むことで、正弦波の式の理解が深まるとともに、逆向きに波が動く場合の式、初期位相がある場合の式、そして、グラフの読み取りもできるようになります。
目次
正弦波とは?

まず、正弦波というのがどんなものかを理解しておきましょう。
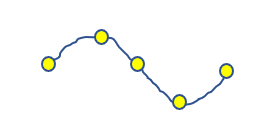
例えば、図のようにいくつかの玉を糸でつないで上下に振動させてみます。
すると、次々と玉が振動していきますね。この球を大量に、無限につなげていくと正弦波になります。

波の正体は、無限個の物体を単振動させてものなのです。
ちなみに、この話を実際の入試問題で問われることもあります(東工大で出されたこともあります)。
ですから、正弦波のある点を見ると、その点の高さは単振動の変位の式と同じ形になっているわけです。
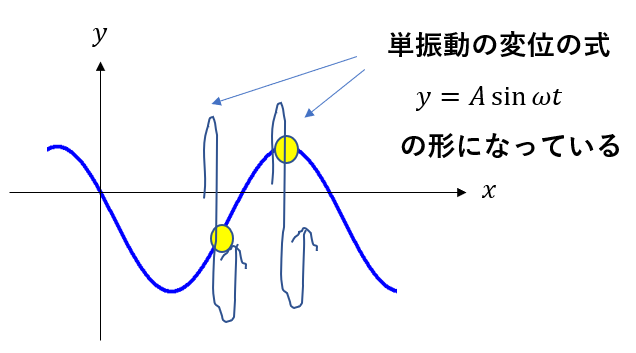
ただ、今まで単振動と言えば、基本的に1物体のばねの運動を見ていくのが普通でしたね。
なので、変位の式もその物体に関して考えればよかったのです。
\(y = A\sin{\omega t}\)と時間\(t\)だけの式で表すことができました。
ですが、波は先ほども言ったように無限個の物体の集まりです。つまり、各点ごとに式が違うはずですよね。
なので、時間\(t\)だけで式として表すことができないのです。
そこで、位置\(x\)という情報を式に入れることで、
「位置\(x\)にある点が、時間\(t\)でどの高さ\(y\)にあるか」
を考えて、式に表してみるのです。
正弦波の式 → ある位置\(x\)の物体がある時間\(t\)でどの高さにある?
原点にある波の点は、時刻\(t\)において変位が\(y = A\sin{\omega t}\)と表されている。また、波はx軸正の向きに速さ\(v\)で伝わる。このとき、ある位置\(x\)にある点は、時刻\(t\)において変位はいくらであるか?式に表してみよう。
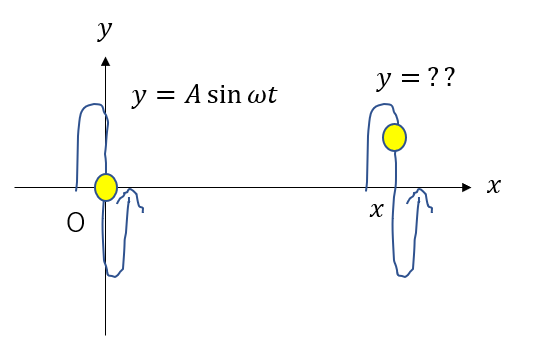
時間を戻して考える

今、原点の位置\(x = 0\)にある点は式として表されています。
ですから、位置\(x\)にある点は、この原点にうまく対応させることで式に表すことができるのです。
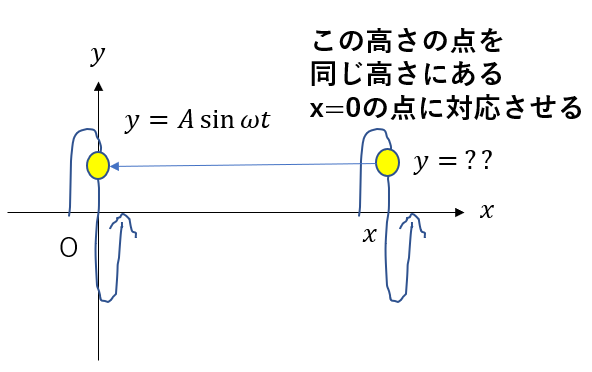
位置\(x\)にある点は、\(x = 0\)にある点が、ある時間\(t_0\)かけて伝わったものです。
ですから、\(t_0\)だけ時間を戻すことで原点に対応させることができ、最初に与えられた式を使って位置\(x\)にある点の変位がわかるのです。
この\(t_0\)を求めてみましょう。
これは簡単で、距離\(x\)を速さ\(v\)で進むわけですから
\(t_0 = \frac{x}{v}\)です。
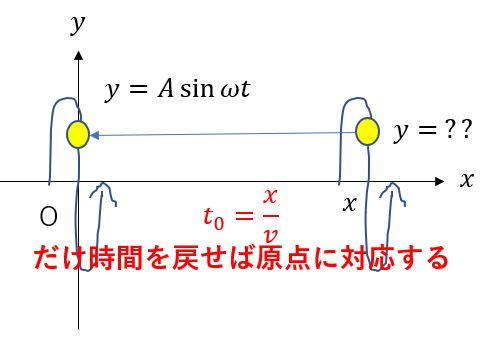
ということで、\(t\)を\(t – t_0\)に置き換えることで、位置\(x\)における変位を導くことができます。
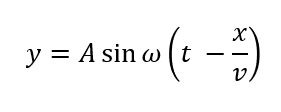
これが正弦波の式になります。
最初の言ったように\(t\)だけでなく、\(x\)も含まれていますね。
波は無限に点があるので、このように\(x\)の情報が含まれているのです。
波が逆向きに進む場合は?

今、波が\(x\)正向きに進む場合を考えました。しかし、もちろん負向きに進む場合もありますよね。
これも考えてみましょう。
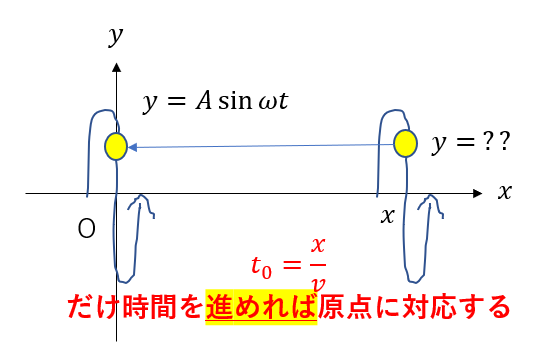
今度は図のように、時間を進めることで原点に対応させることができます。
つまり\(t\)を\(t + t_0\)に置き換えればいいのですね。
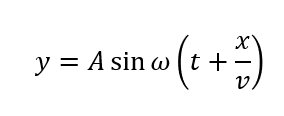
符号が変化するだけですね。
ちなみに、逆向きなので\(-v\)と置き換えると考えてもやはり同じ結果になりますね。
正弦波の式の式変形

この波の式ですが、いろんな形に式変形できます。これもできるようにしておきましょう。
まず\(\omega\)というのは「角振動数」です。円運動で言うと「角速度」ですね。
これは周期\(T\)と次のような関係があります。
\(\omega = \frac{2\pi}{T}\)
これを使って正弦波の式を置き換えることができます。
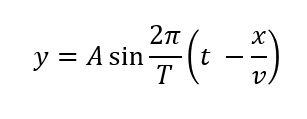
また、\(Tv = \lambda\)という関係を使うことで次のように式変形もできます。
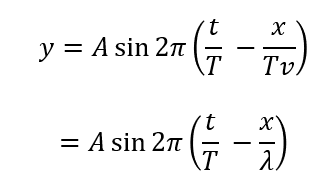
覚える必要はありませんが、式変形を自分でできるようにしましょう。
正弦波の式は「波そのものを表す式」ではない!

この正弦波の式ですが、「波形を表す式」だと勘違いしている人が多いです。
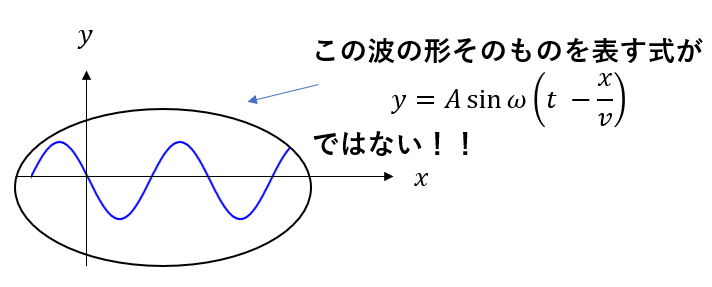
波形を表すのはあくまで図のようにy-xの関係で見た場合の話です。つまり、\(t\)を何らかの値にして考えた場合のものになります。
正弦波の式はグラフと関連付けてしっかり理解をしておく必要があります。
詳しくはこちらを確認してください。
初期位相がある場合

最後に初期位相についてお話をしましょう。
そもそも位相とは?というところを簡単にお話しておきましょう。
単振動や波を図に書こうとすると、ある点がどちらに動くかが見えにくくなるという問題が発生します。
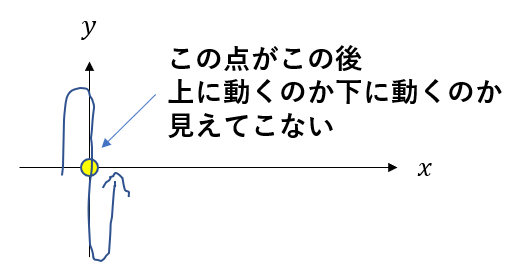
上に動くか、下に動くかって重要ですよね。その違いを表すものが「位相」です。
単振動はもともと円運動から来ていましたね。
詳しくはこちらを確認してくださいね。
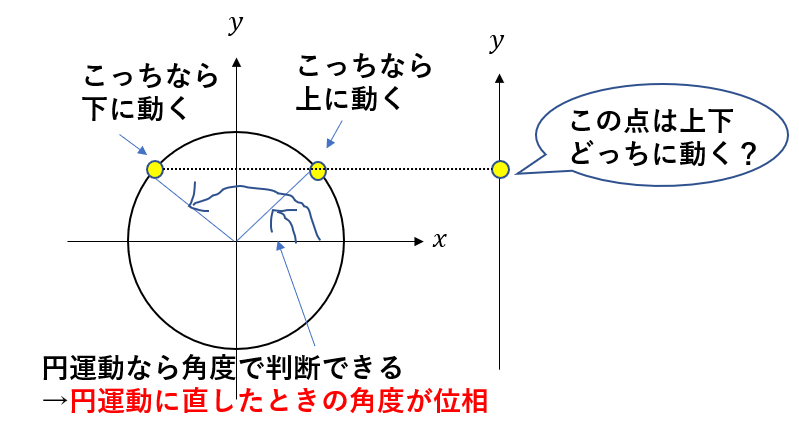
単振動は円運動を一つの軸だけに関して見たものなので、円運動では明らかに違う点でも、単振動では同じ位置の点になり、「どちらに動くか問題」が発生してしまうんですね。
ですが逆に言えば、単振動を改めて円運動に直せば円運動の角度を見ることでこの問題を解決できます。
この「円運動に直したときの角度」を位相と言い、単振動のある点の状態を知る手掛かりになるのです。
そして、位相は式のsinやcosの中身に現れてきます。
特に、\(t=0\)つまり最初の段階での位相を初期位相と言います。
これを踏まえて先ほど、正弦波の式を出した例をもう一度見てみましょう。
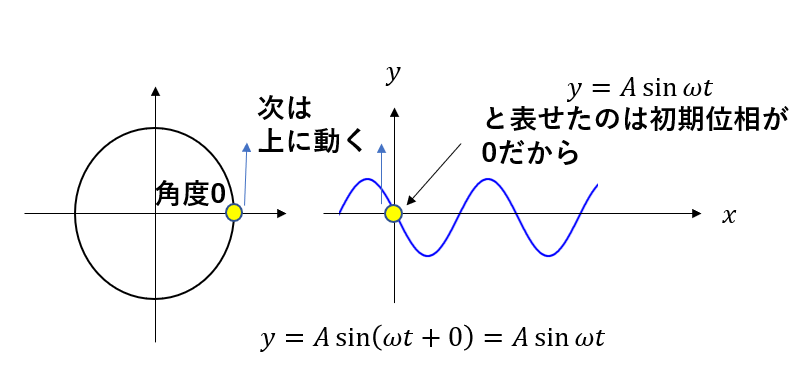
先ほど正弦波の式を導いたとき、原点における変位の式を
\(y = A\sin{\omega t}\)
と勝手に置きましたが、初期位相が0だったからです。
もし次のような場合だったどうでしょう?
\(t =0\)で図のような波形の波がある。右向きに速さ\(v\)で伝わるとき、位置\(x\)における時刻\(t\)のときの変位を角振動数\(\omega\)を使って表せ。
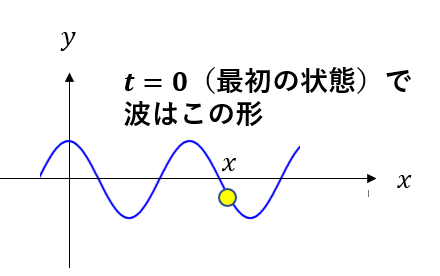
まず、原点をよ~く見てください。
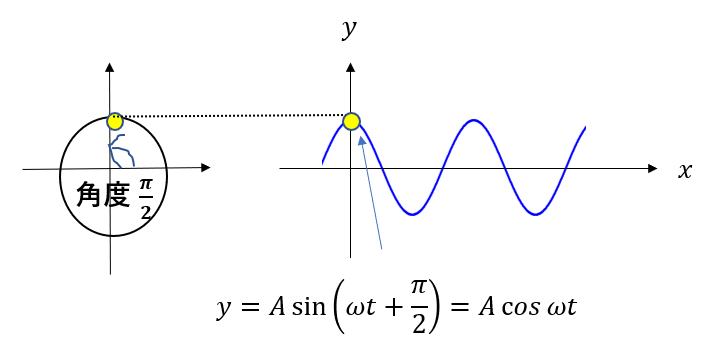
初期位相が0ではありませんね。\(\frac{\pi}{2}\)だけ進んでいます。
つまり、原点では
\(y = A\sin{(\omega t + \frac{\pi}{2})} = A\cos{\omega t}\)
と表されるのです。
このように、\(x = 0\)での初期位相をしっかり見ないと、正弦波の式を導く際に間違えてしまいます。
正弦波の式を求めさせる問題は多くはありませんが、出ることは十分にあり得るので気をつけましょう。
別で問題演習もしていきましょうね。
まとめ:正弦波の式に覚え方はありません

いかがでしたか?
正弦波の式は覚えるものではないことが分かったかと思います。
初期位相によってsinにもcosにもなるので、自分で導出できるようにしてくださいね。
正弦波の式
原点に時間を戻したり、進めることで対応させる
*初期位相によって式の形が変わってしまうので初期位相もしっかり考慮する
3単元に絞った究極の解法をたった2週間で手に入れ40点アップさせる波動プログラム開講中!










Comment
こんにちは!
質問というより指摘に近いのですが、原点はyが必ずしも0になる訳ではないので「原点に戻して考える」というより「x=0に戻して考える」の方が表現としては正確ではないでしょうか。
また、波がx軸負方向に進むときの考え方を教えてください!
「x=0に戻して考える」の方が正確かもしれませんね。ご指摘ありがとうございます。
波がx軸負の向きに進むときも全く同じ図を書いて考えてみてください。
さっきは「xの位置からx=0の位置まで戻す」でしたね。右向き(正向き)に進んでいたので「戻す」わけです。
では、左向き(負向き)に進んでいたら??
「xの位置からx=0の位置まで進める」
ですよね。