物理の系とは？慣性系と非慣性系から学ぶ「系」の本当の意味
どうも！オンライン物理塾長あっきーです
オンライン物理塾長あっきー
問題集に時々出てくる「系」がいまいち分からないです。慣性系と非慣性系の「系」です。
リケジョ志望のAIさん
問題集などで「1つの系」という言葉を見かけたり、授業で「慣性系」と「非慣性系」という言葉を習いませんか？
共通して「系」という言葉が含まれています。
学校ではこの物理の「系」の説明を詳しく教えてくれませんね。
ですが、この「系」はめちゃめちゃ大事です。なんとなくで理解している人も図と式の2つの観点から「系」を理解することができます
この記事では、「物理の系」の意味を明らかにして、入試で使える「系」の例を教えていきます。
最後まで読むことで、物理の複雑な問題も解けるようになり、ライバルと差を広げられます！
「物理の系」の意味が分かる
入試で使える「系」が分かる
入試レベルの複雑な問題が解ける
目次
物理の系とは？
結論から言うと、「系」の意味は
物体の見方
です。
物体を見る方法はいろいろありますよね。
複数の物体をひとまとまりにしてみる→１つの系（質点系）
重心から見る→重心系
加速度せずに見る→慣性系
加速度運動しながら見る→非慣性系
慣性力を学ぶときに「慣性系」と「非慣性系」という言葉は教科書や学校で出てきたかと思います。
慣性系と非慣性系にも「系」という文字が含まれていますので、物体の見方を表しているだけです。
観測者が床に静止して物体を見るのか、電車に乗って物体を見るのか？
このように物体の見方を表しているのが「系」なのです。
物理の系を使うと式も変わる
物理の系は見方の違いということが分かりました。
そして、見方が変わると実際に使う式にも違いがみられます。
例えば慣性系と非慣性系です。
慣性力のところでさらっと出てきましたね。これらの違いは上に示した通りです。
加速度せずに見る→慣性系
加速度運動しながら見る→非慣性系
慣性系であれば、運動方程式は\(m\vec{a} = \vec{F}\)で良いんですが、
非慣性系では、慣性力\(\vec{F_0} = -m\vec{a_0}\)を補正して
\(m\vec{a} = \vec{F} + \vec{F_0}\)
として運動方程式を立てなければいけませんでした。
このように、系によって式も変わってきます。
見方を変える＝式変形
物理は面白くて、実際に図でイメージしたことと式変形したものがリンクしています。
例えば、相対速度を考えるときは
\(\vec{v_{AB}} = \vec{v_B} – \vec{v_A}\)
のように、「自分の速度を\(\vec{v_A}\)で引く」という式変形が「Aから見たBの速度」と対応しています。
また、「物体を1つの系として考えること」も「2式を足すこと」と対応しています。
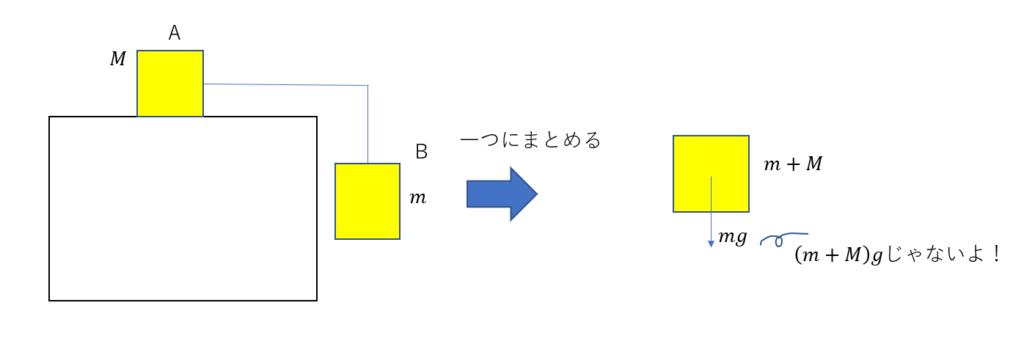
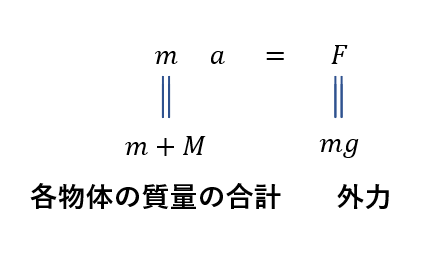
これに関しては系の具体例を出すときに詳しくお伝えします。
物理の系を使うメリット
見方がいろいろあると言っても、動いて見たら複雑になりませんか？式も変わっちゃうし・・・
リケジョ志望のAIさん
実は系をうまく使うことで物体の運動を単純化できる場合があるんだ。
オンライン物理塾長あっきー
例えば図のように2物体がばねでつなげられていて、これを右にはじいてみるとどんな運動になるでしょう？
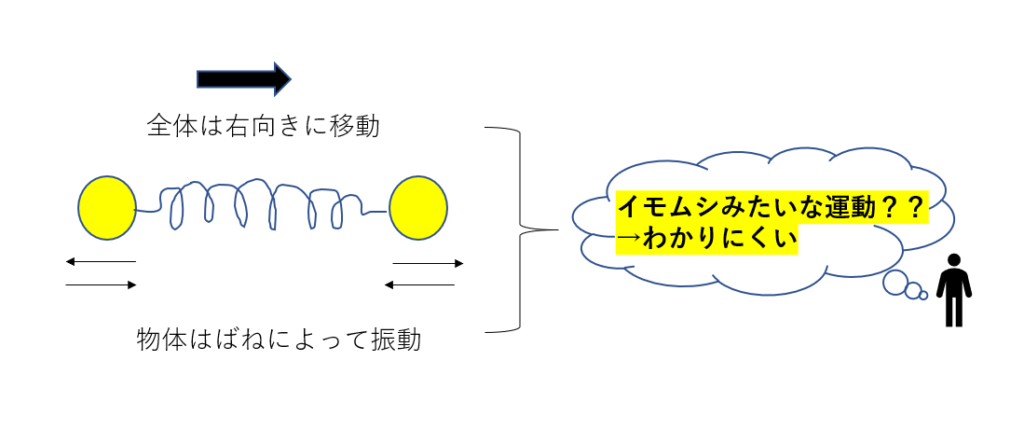
床に静止した人から見ればイモムシみたいな運動になりますよね？
ある程度イメージはできても式でいろいろ考えるのは難しそうですよね？
ですが、これをある見方で考えると「等速運動」と「単振動」に運動を分けることができます。
（その見方は後程お伝えします）
入試で使える物理の系4選
なるほど。系は味方のことで、これを使うと簡単になる場合があるんですね。
リケジョ志望のAIさん
そう！そして入試で使える物理の系を4つ紹介しますね。
オンライン物理塾長あっきー
物理の系を習得しておくと、上のような激ムズ問題（いわゆる二体問題）も楽々解けるようになります。
1つの系でみる（質点系）
例えば2物体の問題を扱った問題で問題集の解説でたまに出てきます。
例えば糸でつなげられた物体について加速度を求めるとき、運動方程式を使うのですが、1つ1つ立てるのが面倒！
そんな時に使えます。
この、2物体をまとめて考える見方を1つの系で見ると言います（一般的には質点系と言います）
1つの系に関してはこちらで分かりやすく解説しているので確認してください。
相対系
物理の初めに相対速度を学んだかと思います。
あれも「系」ですよね。「Aから見たBの相対速度」というのは「Aと同じ動きをしてBを見たときの速度」と言い換えられます。
これをこのサイトでは相対系と呼んでいます。
相対系にはある重要な考え方があります。
「止まって見る場合に置き換えたとき補正する」という考え方です。
これだけだと何を言っているか分からないと思うのでこちらの記事をチェックしてくださいね。
非慣性系
非慣性系は相対系の1つです。
相対系は「動いて見る」場合なら何でも良かったんですが、非慣性系は「加速度運動して見る」ことです。
加速度運動して見る場合は慣性力がはたらきます。つまり、運動方程式を使う際に考える系です。
相対系の一種ですから、これも「止まって見る場合に置き換えたとき補正する」という考え方が大事です。
慣性力、非慣性系について詳しくはこちらの記事を読んでください。
重心系
重心系も相対系の一つです。相対系の中でも限定して、「重心から見る」ことです。
先ほどみせた、イモムシのような運動（二体問題）を解く際に絶対に必要となるものです。
これを知っているかどうかで難易度が大幅に変わります。
というより解けるか解けないかが決まります。
重心系に関してはこちらの記事で詳しく解説していますのでチェックしましょう！
まとめ：物理の系の考え方を理解しておこう
いかがでしたか？
物理の系は学校ではまず教えてくれません。
教科書や参考書でも深く教えてくれないでしょう。
しかし、重心系など知らないと100％解けないような問題もあります。そしてこのような難しい問題は入試問題を作るにはもってこいなんです。
ですから、この系という概念を理解しておきましょう！！
