【まとめ】高校物理の波動の公式まとめ。問題を解くコツを大公開します!

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
私波動が苦手なんです。波動の問題で意識すべきことってありますか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
波動は高校物理の中でも難所でして、苦手という受験生は非常に多いです。あなたもそうではありませんか?
確かに波動の問題はイメージがしにくく、解く以前に意味が分からないことも多いです。
しかし、波動の問題のパターンというのは決まっていて、コツも存在します。
この記事では、波動の公式をまとめつつ、波動の問題の解き方を一気に公開していきます。
最後まで読むことで、「波動ってやってること一緒じゃん!」という感覚がつき、模試などの初見問題も解けるようになります。
波動分野の公式が一気に分かる
波動分野の問題の解き方が分かる
目次
波動分野の問題は3つある

波動の中には大きく3つの単元があります。各単元で出される割合は次のようになります。
国公立 (%) 私立(%) 波の性質 4.0 4.1 音波 7.9 7.5 光波 9.1 6.6 (セミナー物理・物理基礎 2016 大学入試問題の分析と対策(物理))
国公立と私立で若干違いますが、光波 > 音波 > 波の性質という順に出題率が大きいです。僕も過去問を解いていく中で圧倒的に光波・音波は多かったです。
ですが、これでは単元の中で何を問われるかが分かりませんね。
実は各単元の中で出されるものがある程度決まっています。
波の性質→正弦波の式

波の性質で問われるのはほぼ間違いなく「正弦波の式」です。
光波や音波に比べて影が薄い分、「正弦波の式を忘れてた!導出方法も分からん!」となってしまいがちです。(僕も東京理科大の入試で正弦波の式が出て、全く解けませんでした(泣))
正弦波の式そのものについて問われたり、グラフと組み合わせて問われることが非常に多いです。
音波→ドップラー効果

音波の単元は「ドップラー効果」が圧倒的に多いです。
反射板を使ったドップラー効果の問題は難関大なら基礎レベルです。
ドップラー効果の公式を覚えるのは良いのですが、意味を理解していないと解けないような問題が出てきます。
2次試験では、一直線上にない場合のドップラー効果だったり、円運動とドップラー効果の融合問題、さらにはドップラー効果の導出について問われます。
光波→光の干渉

光波では干渉問題がダントツ多いです。光、いや、音波だろうと何だろうと波動分野で干渉問題はめちゃめちゃ問われます。
授業でやる内容の中では、ヤングの実験や回折格子の問題多いです。
しかし、難関大レベルではこれくらいは当たり前で、見たことない状況での干渉問題が問われます。
過去問などで出てきたものをパターン化して覚えるには数が多すぎるので、暗記でどうこうできるものではありません。
波動分野の公式まとめ

この3つを優先的に伸ばしていく必要があります。
そこで、この3つに関して使われている公式をまとめていきます。
正弦波の式
正弦波の式はこのように表されます。
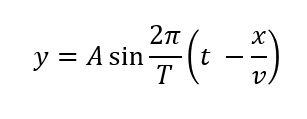
\(A\):振幅、\(T\):周期、\(v\):速さ、\(\lambda\):波長
これは覚えるのではなく、必ず導出もできるようにしてください。
導出方法は以下の記事で詳しく説明しているのでこちらを確認してください。
ドップラー効果

ドップラー効果の公式はこのように表すことができます。
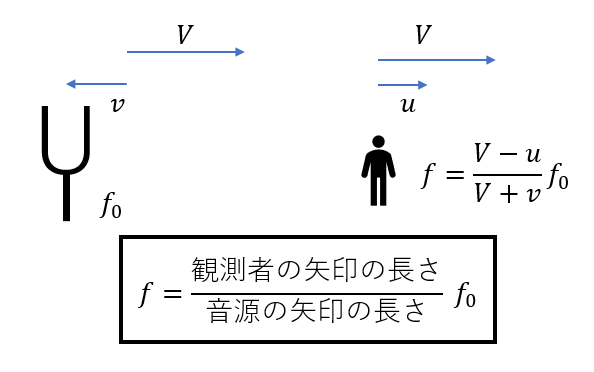
観測者・音源が動く速度の矢印、
観測者・音源の音速の矢印
これらの長さを式に当てはめるのです。
やはりこれも導出方法を知っておくべきです。
ドップラー効果の公式に関しては詳しく以下で説明していますので、こちらを確認してください。
光の干渉

波の干渉条件を表す式はこちらです。

経路差が半波長の偶数倍なのか奇数倍なのかで判断します。
波長ではなく半波長を使うことで、条件式が分かりやすくなるのです。
これまた、導出方法もセットで覚えてください。
干渉条件についてはこちらで詳しく説明しています。
導出しつつ、使いながら覚える

公式はここでまとめましたが、必ず自分で導出できるようにしてください。これにより公式の意味を理解することができます。
また、公式を頭に叩き込むのではなく、使っているうちに覚える感覚を身に付けてください。
単語のように必死に覚えると絶対に忘れます。公式は「使う」ものです。
問題を解いていく中で、自然に覚えるようにしましょう。
波動分野の問題を解き方

最後にここまで見てきた単元の問題をどのように解いていくかをまとめていきます。
これを見れば「コツ」が分かり、初見問題でも対応できる力が身に着きます。
正弦波の式はグラフと関連させて突破できる
正弦波の式の問題の解くコツはたった2つです。
- 正弦波の式の導出する
- 「式→グラフ、グラフ→式」の変換をできるようにする
正弦波の導出は式の意味を理解するために必要です。
そして、正弦波の式はほぼ間違いなくグラフとセットで出てきます。
「グラフから正弦波の式のどこの情報が分かるのか?」あるいは「正弦波の式からどんなグラフが書けるのか?」というのをクリアすることで正弦波の式を攻略することができます。
正弦波の式とグラフに関しては以下に詳しく書いてあるのでチェックしましょう!
ドップラー効果の問題はやることが決まっている

ドップラー効果の問題は先ほどの公式がすべてなんですが、応用問題向けにポイントが2つあります。
- 反射板は「観測者」と「音源」の両方になる
- 斜めにある場合は分解する
反射板のある場合、一直線上にない場合、円運動する場合などさまざまな状況でドップラー効果があります。
反射板の場合は「受け取る→放つ」の両方を行うためそれぞれ「観測者」と「音源」とみなして公式を適用します。
一直線上にない場合(円運動も含めて)は、速度を分解するなどして直線になる方向に関して考えます。
詳しくは以下の記事でチェックしてください!
光の干渉問題は2ステップで解け

光の干渉問題は2ステップで解くことができます。
- 干渉条件を求める
- 条件式から情報を的確に読み取る
干渉の問題は初見ばかりです。初見でなくても「ヤングの実験でガラスを挟む」などのいろいろ条件を変えて出されることが普通です。
初見問題を出された途端、何をすべきか分からなくなってしまったり、やったことのない方法で解こうとしてしまいます。
ですからこの2ステップを頭に入れておいて各問題で適用できるようにする訓練を積みましょう。
以下で「ヤングの実験のガラスを置く問題」を解説していますのでチェックしましょう。
波動分野がどうしてもできないときは

波動分野は苦手が多いところです。僕のところにも波動分野が苦手だというメッセージはよくきます。
正直なところ、できない人はとことんできないのが物理です。
「1人ではどうしようもない!」
そのような方はぜひ、僕が開いている波動プログラムにご参加ください。
波動のノウハウを教えるだけでなく、個別にLINEで質問対応しますし、コンサルも行います。
波動で、そして物理、さらには勉強に関して悩んでいる人はぜひこちらのプログラムに参加してください!あなたを全力でサポートします。
まとめ:3単元をまずは集中攻略

いかがでしたか?
もちろん、波動の分野にも弦の振動やレンズなどはあります。ここで紹介したものがすべてではないです。
ですが、問われる確率が少ない問題と確率が高い問題、どちらを優先して勉強すべきかというと絶対に確率の高い問題ですよね?
ここで紹介した問題はすべて出されやすい問題です。
ここで紹介した問題をまずは攻略することを目標に勉強を進めていきましょう。









