合成抵抗の求め方。複雑な問題でも求めるコツを大公開します!

どうも!オンライン物理塾長あっきーです
 あっきー
あっきー
合成抵抗って回路が複雑になると求められなくなります!何かコツってありませんか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
この悩みを解決したいと思います。
合成抵抗を「直列だから和」「並列だから逆数の和」のように覚えている人が非常に多いです。
直列・並列でパターン化すると複雑な回路になったときに絶対間違えます。
直列・並列ではなく、絶対に間違えない分け方があるのです!
この記事では合成抵抗の求め方を解説し、複雑な回路になった場合の合成抵抗を求める方法教えます。
合成抵抗の意味が分かる
合成抵抗の求め方が分かる
直列・並列に代わる分け方を理解できる
複雑な回路の合成抵抗をミスなく求められる
目次
合成抵抗とは

合成抵抗とは複数の抵抗を1つにまとめることです。
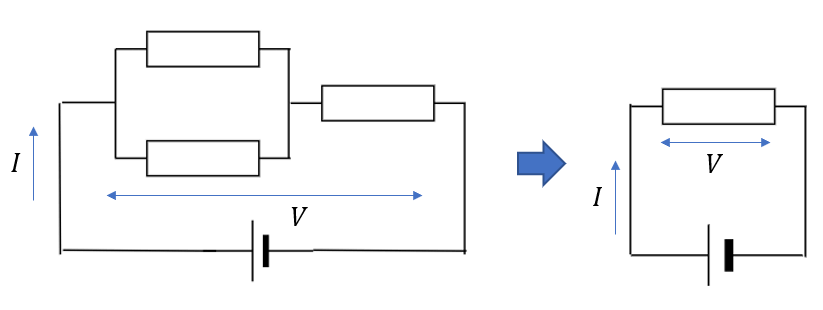
左図のように複数抵抗があるとややこしいですよね。
これを回路の性質を変えないで右のように変えられたら楽ですよね。
「回路の性質を変えないように回路を変形する」ことを等価回路と言います。
全体に流れる電流\(I\)や電圧\(V\)は変わらないように抵抗を置き換えたとき、この抵抗を合成抵抗と言います。
合成抵抗の求め方

どんなに複雑な回路でも抵抗のつなぎ方は2通りしかありません。
「直列」「並列」だけです。
つまり、直列と並列それぞれの場合で合成抵抗を求める方法が分かれば良いのです。
そこでこの2つに分けて合成抵抗を求めてみましょう。
合成抵抗を求める手順

合成抵抗を求めるには、先ほど言ったように等価回路を考えます。
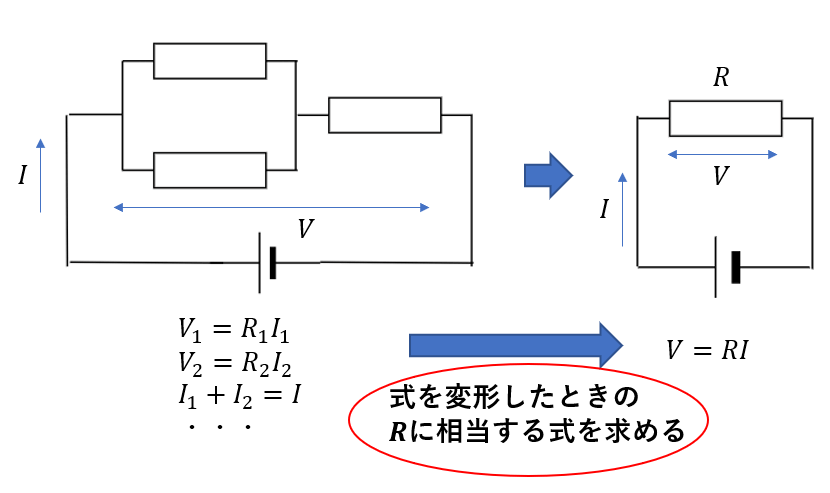
元の回路で成り立つ式を考えて、一つの抵抗に置き換えた回路で成り立つ式\(V = RI\)の\(R\)に相当する式を求めれば合成抵抗になります。
式を考えるには、当然ですがキルヒホッフの法則を使います!
そして、スタートとゴールをきっちり定めることが合成抵抗を求める上で大事です。
合成抵抗の求め方1:直列接続
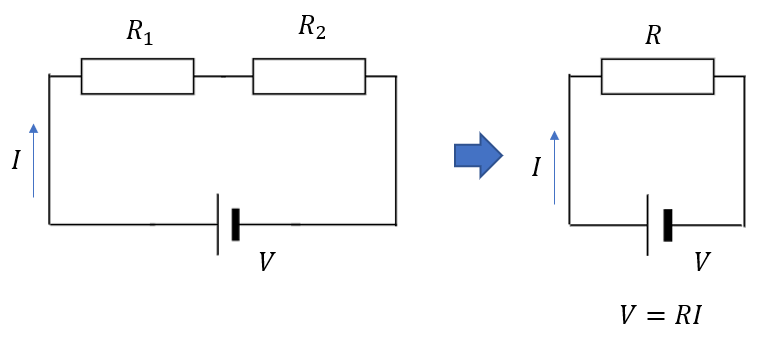
まずはスタートとゴールの図を書きます。
性質は変えてはいけないので電源の電圧も電源から流れる電流も同じ大きさである必要があります。
そして最初の回路で成り立つ式を出していきます。
- 電圧マークを書く
- 1周した電位=0
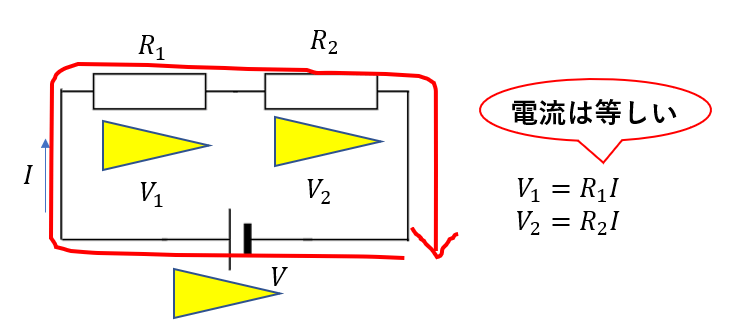
直流回路では各抵抗に流れる電流は同じなので
\(V_1 =R_1I, V_2=R_2I\)
と表せます。
そして「1周した電位=0」より
\(V-V_1-V_2=0\)
\(V=(R_1+R_2)I\)
これは求めたかった式の形になっていますね。
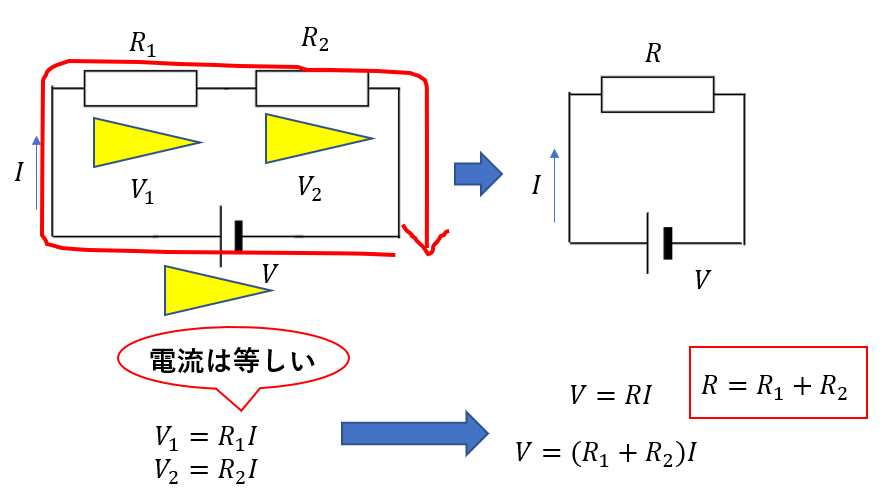
直列では合成抵抗\(R\)は
\(R = R_1 + R_2\)
と表せます。
合成抵抗の求め方2:並列接続
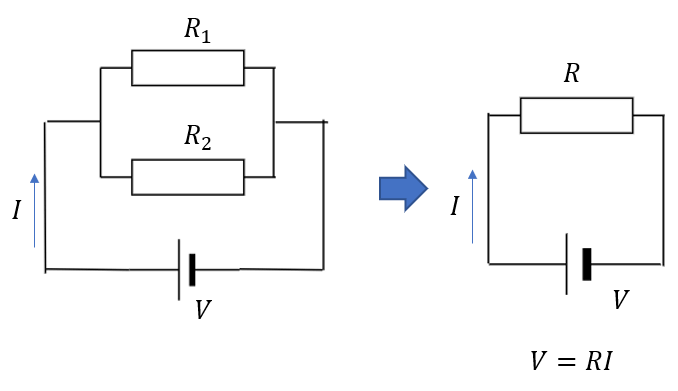
直列と同様、まずはスタートとゴールを決めます。
性質は変えてはいけないので電源の電圧も電源から流れる電流も同じ大きさである必要があります。
元の回路から得られる式を考えますが、キルヒホッフの法則を使うと各抵抗にかかる電圧は電源の電圧と等しくなることが分かります。
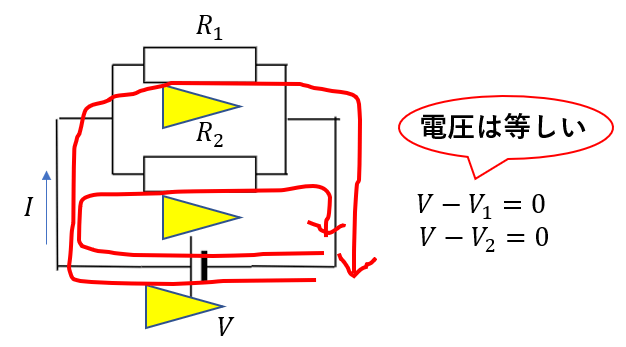
そして、各抵抗に流れる電流\(I_1,I_2\)とすれば
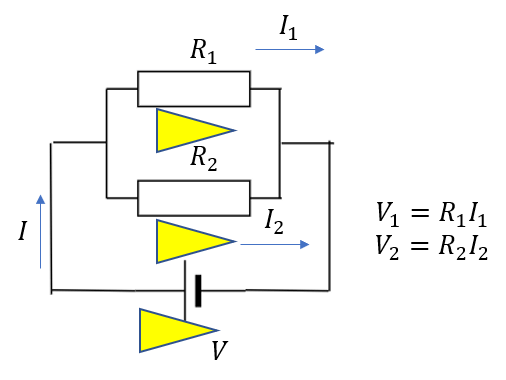
\(I=I_1 + I_2\)ですからこれらをまとめるとこのような式が得られます。
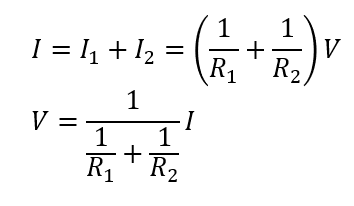
これは求めたい形\(V =RI\)になっていますよね。
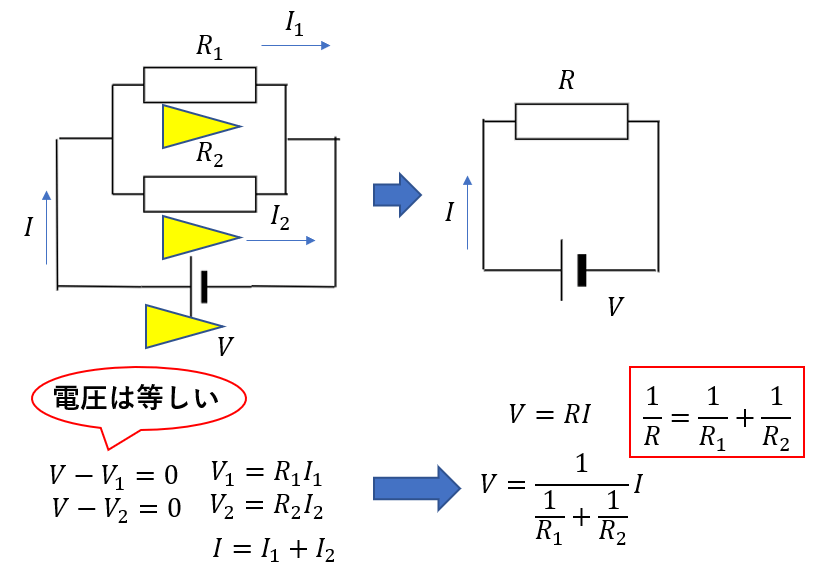
少しわかりにくいですが\(\frac{1}{R} = \frac{1}{R_1}+\frac{1}{R_2}\)と置けば\(V=RI\)の形になることが分かります。
並列では逆数の和を取ってその逆数を取るんですね。
いちいちこれを計算するのが面倒なので、
\(R = \frac{R_1R_2}{R_1+R_2}\)
と考えても良いですね。
\(\frac{積}{和}\)と覚えておくと計算が早く、ミスも減りますね。
抵抗が3つ以上ある場合も同じ

この例では2つの抵抗を考えましたが、3つ以上になっても同じです。
2つの抵抗を何回も合成していけば最終的に1つの抵抗に合成できます。
直列の場合は
\(R = R_1 + R_2 + + … R_n\)
並列の場合は
\(R = \frac{R_1 R_2 … R_n}{R_1 + R_2 + … R_n}\)
と一般に表すことができます。
合成抵抗は電流・電圧のどっちが同じかで分ける

このように直列と並列で合成抵抗を求めることができました。
しかし、直列と並列で分けてしまうとイタイ目にあうことが多いです。
直列と並列で考えるとミスが起こる
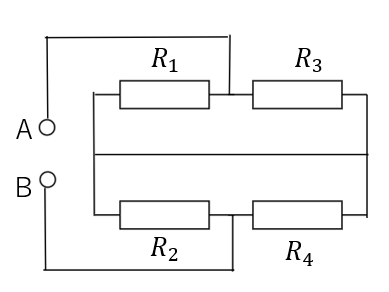
「ABを電源とするこの回路の合成抵抗を求めよ」
と言われたら求められますか?
どこが直列でどこが並列か一発でわかりますか?
ちなみに、\(R_1\)と\(R_3\)、\(R_2\)と\(R_4\)はそれぞれ直列・・・
ではありませんよ!

このように回路は変形できます。直列に見えた部分は実は並列だったんですね。
直列と並列で考えてしまうと「形」で見てしまうのでミスが大変起こりやすくなります。
かといって、このようにうまく回路を変形できるかといえば、これまたミスが起こりやすいです。
大事なのは「電流と電圧のどちらが等しいか」
そこで、直列と並列以外の見分け方を教えます。
そもそも直列と並列の定義ってなんだと思いますか?
縦に並んでいる、横に並んでいる
ではありません。
「電流が等しい」ときが直列で、「電圧が等しい」ときが並列です。
そうです。あなたは絶対にこう思っていたはずです。
直列→電流が等しい
並列→電圧が等しい
違います。逆です
電流が等しい→直列
電圧が等しい→並列
つまり、「直列か並列」ではなくて「電流と電圧のどっちが等しいの?」と考えるべきなんです。
こうすることで合成抵抗を求めるのに圧倒的にミスが減ります。
合成抵抗を複雑な回路で求めるコツ

複雑な回路で合成抵抗を求めてみましょう。
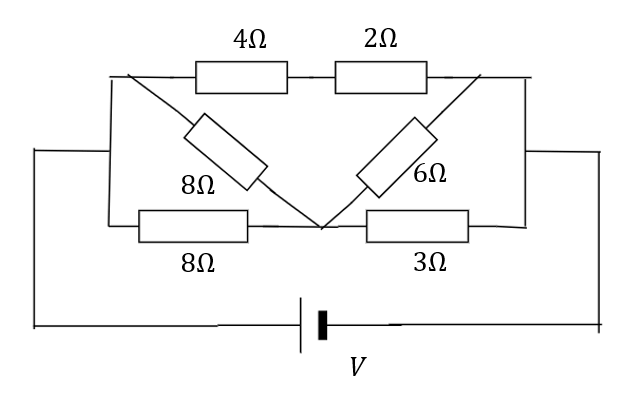
どれが直列でどれが並列か見分けがつかないですよね。
そこで電流が等しいか電圧が等しいかを見ます。
電流が等しい部分
電流が等しいのは分岐点が無いところです。
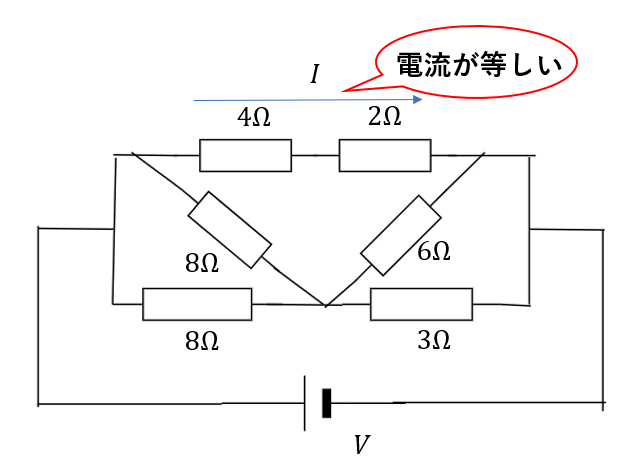
図の部分には分岐点が途中なく抵抗がつながっているので、電流は等しくなります。
電圧が等しい部分
電圧が等しい部分は閉回路を1周した時に抵抗がちょうど2つある部分です。

1周する間に抵抗がちょうど2つだけあればキルヒホッフの法則から2つの抵抗の電圧は等しくなりますよね。
なので2つ抵抗がある部分を探すのです。
条件に合わせて合成抵抗を求める
後は合成抵抗を求めるだけです。
電流が同じなら和、電圧が同じなら\(\frac{積}{和}\)です。
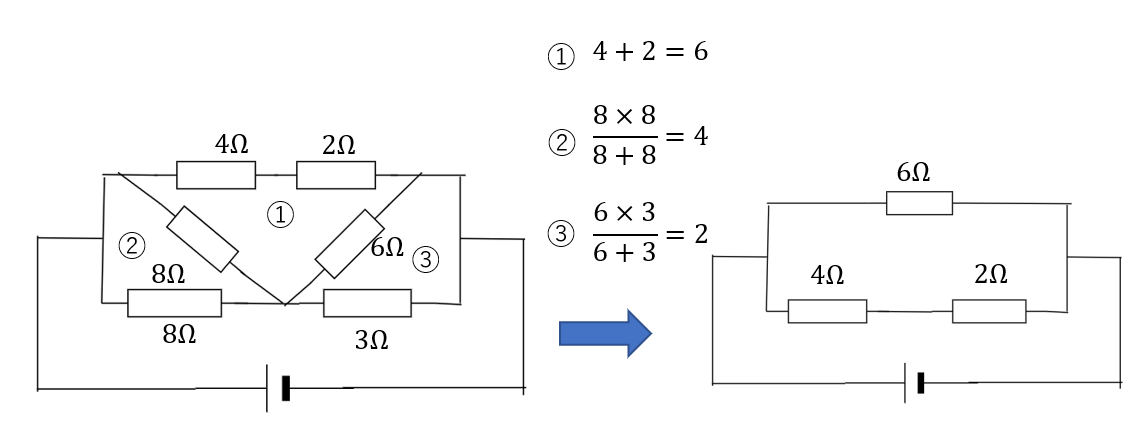
合成したものは1つにまとめて整理します。
ここまで合成できれば回路がきれいになりましたね。最後も合成は大して難しくありませんね。
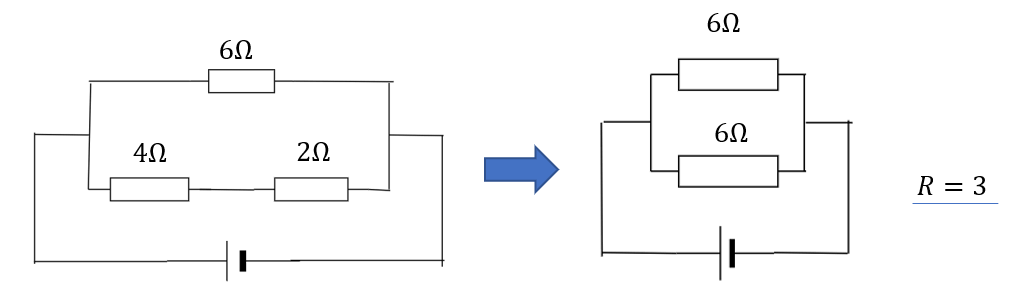
合成抵抗は\(R=3\)となります。
このように電流と電圧のどっちが等しいか?という観点で見れば複雑な回路になっても合成抵抗は求められます。
合成抵抗は公式で覚えてはいけない

合成抵抗を公式のように求めていましたが、本来は公式で覚えるものではありません。
「抵抗をまとめて簡単な回路にするには?」と考えたときにたまたま現れた式です。
回路問題としてキルヒホッフの法則を使って求めているに過ぎないのです。
まずは自分で導出できるようにします。それを繰り返しているうちに自然と式が頭の中に入ったという感覚が一番いいのです。そこを目指してください。
そのほかの合成

合成については抵抗以外にもあります。
ばねの合成、コンデンサーの合成、インピーダンス
が主にあります。
これらも考え方は合成抵抗と同じなのでこの機会にすべてマスターしましょう。
まとめ:電流と電圧のどちらが同じかで分ける

いかがでしたか?
合成抵抗の意味も理解でき、直列と並列の考え方も驚きだったのではありませんか?
今回の内容を必ず復習してバシバシ問題演習をこなしてくださいね。
合成抵抗
電流が等しい→\(R = R_1 + R_2\)
電圧が等しい→\(R=\frac{R_1R_2}{R_1 + R_2}\)









Comment
複数並列の合成抵抗の式間違えてます