単振り子の運動方程式の立て方と周期の求め方【ただの単振動です】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
今回は単振り子を見ていきます。
単振り子を難しく考える人が多いのですが、単振り子は単振動の一種です。
つまり、単振動の知識があれば問題なく理解できます。
一つテクニックとして近似が出てきますが、それもこの記事で理解できますので最後まで読んでくださいね。
単振り子の原理
単振り子の運動方程式の立て方
目次
単振り子とは?
単振り子とは次のように円運動のごくごく小さい範囲で起こる振動です。
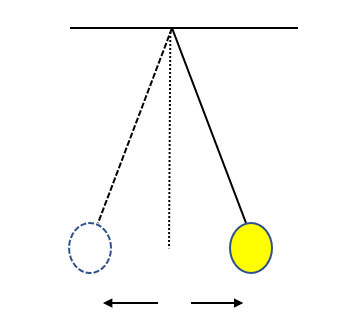
円運動ですが、近似的に直線運動とみなして単振動として考えることができます。
では、この振り子の周期を求めていきましょう!
単振り子の運動方程式
単振動にもっていきたいので、
運動方程式
↓
単振動の条件式
↓
単振動の3つのステップ
この流れを意識しましょう。単振動についてはこちらをご覧ください。
単振り子の運動方程式を立てる
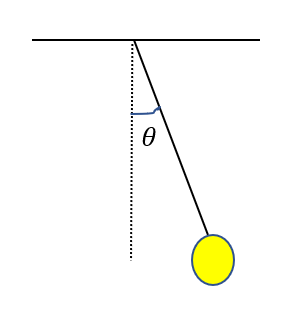
図のように、鉛直方向から角度\(\theta\)にある物体の運動方程式を立てます。この\(\theta\)は正負を考えます。反時計回りを正としますね。
イメージ的に鉛直軸を中心に単振動しそうですね。ばねの単振動でもやったように場合分けをして考える必要がありそうです。
\(\theta > 0\)のとき

まずは鉛直軸より右側\((\theta > 0)\)を考えます。
円運動の接線方向を考えると、力は重力のみですね。その大きさは\(mg \sin{\theta}\)です。
これを成分表示しますが、\(\theta > 0\)なので\(\sin{\theta} > 0\)であり、力は軸と逆向きです。
つまり、成分は負にする必要があるので
\(\vec{F} = (-mg\sin{\theta})\)
と表せます。
\(\theta<0\)のとき
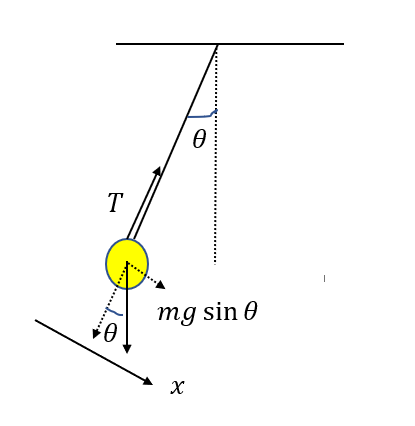
今度は鉛直軸より左側\((\theta < 0)\)を考えます。
円運動の接線方向を考えると、力は重力のみですね。その大きさは\(mg \sin{\theta}\)です。
これを成分表示しますが、\(\theta < 0\)なので\(\sin{\theta} < 0\)であり、力は軸と同じ向きです。
つまり、成分は正にする必要があるので
\(\vec{F} = (-mg\sin{\theta})\)
と表せます。
つまり場合分けをしなくても\(\vec{F} = (-mg\sin{\theta})\)と表せます。
これを踏まえて運動方程式を立てると
\(m\vec{a} = \vec{F}\)
\(ma = -mg\sin{\theta}\)
\(a = -g\sin{\theta}\)
となります。
単振り子では近似を使う
単振り子では\(\theta\)が非常に小さい場合(振れ幅が小さい)場合を考えます。
この場合、円運動は直線運動とみなすことができます。
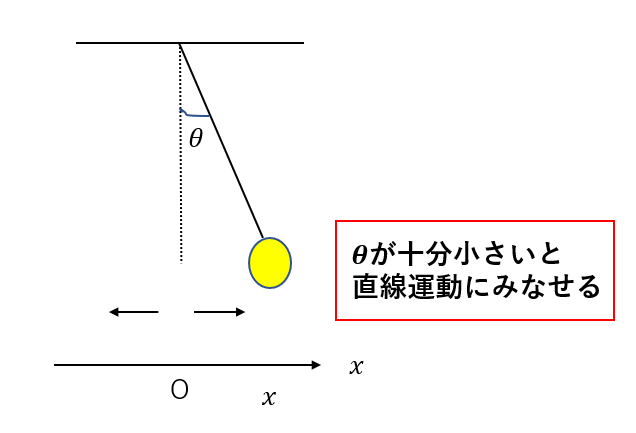
直線運動とみなせるなら、角度\(\theta\)ではなく図のような水平軸\(x\)で考えることができます。
糸の長さを\(l\)と置けば、\(\sin{\theta} = \frac{x}{l}\)となります。
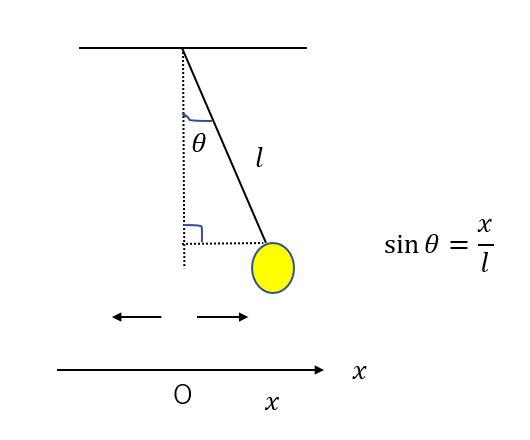
これを先ほどの運動方程式に代入すると
\(a = -\frac{g}{l}x\)
と表すことができます。
単振り子の周期
この式は単振動の条件式に当てはまってますね。
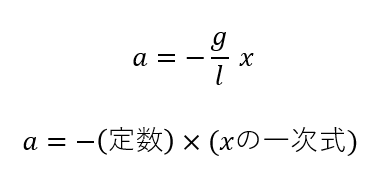
つまり単振動するということが分かりましたね。
後は単振動の3つのステップをやるだけです。
まず、中心\(x_0\)ですが、これは\(x_0=0\)ですよね。
次に、角振動数\(\omega\)ですが、これは\(\omega = \sqrt{定数}\)なので、\(\omega = \sqrt{\frac{g}{l}}\)です。
そして周期\(T\)は\(T = \frac{2\pi}{\omega}\)なので、\(T = 2pi \sqrt{\frac{l}{g}}\)です。
最後の周期をよく見ると、おもりの重さは関係せず、ひもの長さだけで決まることが分かります。
小学校などで実験をしたか分かりませんが、その結果の理由がまさにこれです。
結果ではなくこの流れを説明できるようにしましょう
単振り子は以上です。
正直入試にはあまり出ません。簡単すぎるからです。
大事なのは結果を覚えるのではなく、単振動の流れをしっかりつかみ、単振り子特有の近似ができるようにすることです。
暗記は絶対に止めましょう。
慣性力を用いた単振り子
入試問題では慣性力を使った単振り子の問題が問われます。
これには必勝法があって「見かけの重力」を使うとうまく解けます。
見かけの重力には以外なノウハウが隠されているのでぜひこちらもチェックしてください!
まとめ:単振り子の運動方程式の立て方
いかがでしたか?
正直簡単だったと思います。
単振動自体の復習もしっかりして理解を深めましょう!!
オススメ記事:二体問題を重心で攻略!大学入試で差がつく解き方を大公開!
オススメ記事:合成ばね定数とは?ばねの直列・並列の扱い方を教えます!











