単振動のエネルギーとは?【重力の位置エネルギーは無視できる?】

どうも!オンライン物理塾長あっきーです!センター試験では物理満点をたたき出し、現役で早稲田大学に合格。1年間の塾講師を経験後、月2万人が利用するオンライン塾サイトを運営しています!
 あっきー
あっきー
単振動のエネルギーの使い方がよくわからないです…それになぜ重力の位置エネルギーを無視しているんですか?
 リケジョになりたいAIさん
リケジョになりたいAIさん
今回はこのような悩みを解決していきます。
結論から言うとこうです。
単振動のエネルギーは水平バネ振り子にして考えよ
(位置エネルギーは考慮してます)
単振動のエネルギーは実は重力の位置エネルギーを無視しているわけではなく、すでに考慮しています。
そして、実際に考える場合は水平バネ振り子に置き換えると分かりやすいです。
というわけで詳しく見ていきましょう。
ちなみに単振動の運動方程式の立て方はこちらをチェックしましょう。
目次
単振動のエネルギーとは?

単振動ではエネルギー保存則が成立します。これはばね以外(浮力など)の単振動でも成立します。
そこで単振動のエネルギーを考えるのですが、教科書などではこのように説明されています。
復元力\(-Kx\)の単振動において、力学的エネルギー
\(E = \frac{1}{2}mv^2 + \frac{1}{2}Kx^2\)
は保存される
この\(\frac{1}{2}Kx^2\)が復元力のエネルギーとなります。
単振動のエネルギーで重力に位置エネルギーは無視?
これを見ると重力による位置エネルギーが含まれていないように見えますね。
しかし、重力による位置エネルギーは考慮してあります。ですのでこの式で正しいです。
先ほどの\(\frac{1}{2}Kx^2\)をばねのエネルギーと誤解している人が多いのですが、これはあくまで復元力の位置エネルギーです。
この復元力の位置エネルギーを考える過程で重力の位置エネルギーは考慮されているのです。
単振動の力学的エネルギーの導出

では、この単振動のエネルギーの導出をしていきます。
簡単な例として、鉛直バネ振り子を見ていきましょう。
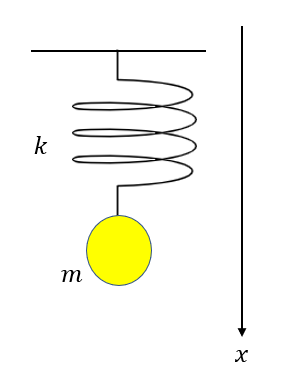
自然長の位置を基準に位置エネルギーを考える
まず、自然長の位置を原点に取ってそこを重力の位置エネルギーの基準にします。
そこからつり合いの位置までの重力の位置エネルギーと弾性力はの位置エネルギーの和\(U_1\)を求めます。
まずつり合いの位置\(x_0\)は力のつり合いを立てればすぐに求まります。
\(mg = kx_0\)なので
\(x_0 = \frac{mg}{k}\)ですね。
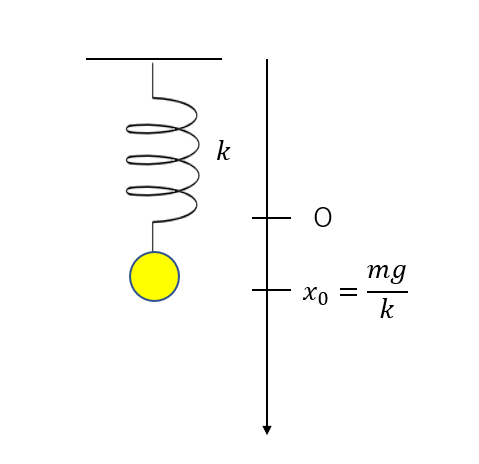
この位置での位置エネルギー\(U_1\)はこうなります。
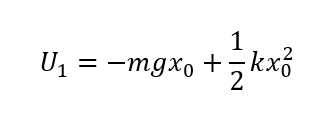
同様に、位置\(x\)における位置エネルギーの和\(U_2\)も考えます。
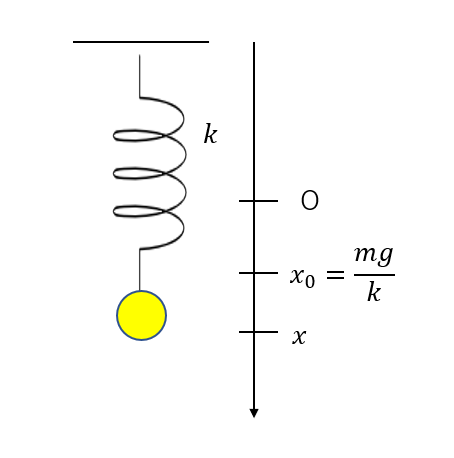
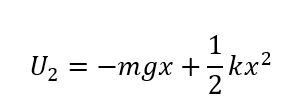
位置エネルギーの基準を振動の中心に合わせる
ここまでは位置エネルギーの基準を自然長に合わせました。
これを振動の中心(つり合い位置)に変換させます。
そのためには先ほど求めた式から\(U_2 – U_1\)で求められます。
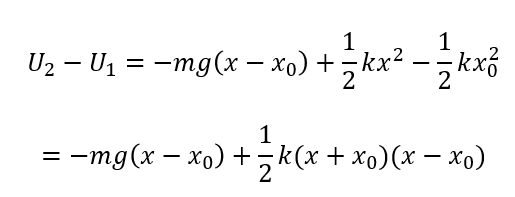
ここで、振動の中心からの位置\(X = x-x_0\)に置き換えて考えます。
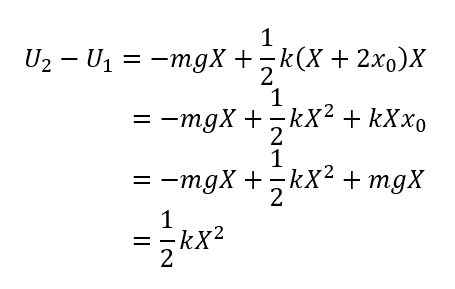
単振動のエネルギー
この式がまさに単振動のエネルギーとなります。
- 重力の位置エネルギーの基準を振動の中心に合わせる
- 振動の中心からの位置で表す
つまり振動の中心で考えることによって重力の位置エネルギーが途中で相殺されたのです。
なので、無視をしているのではなく考慮した結果たまたま消えたという感じです。
これに運動エネルギーをたすと力学的エネルギーとなり、これが一定となります。
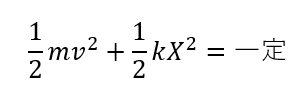
単振動のエネルギーの注意点

単振動のエネルギーは注意点が2つあります。
・振動の中心を基準にした場合に成立
・\(K\)は\(ma = -Kx\)と表したときの\(K\)
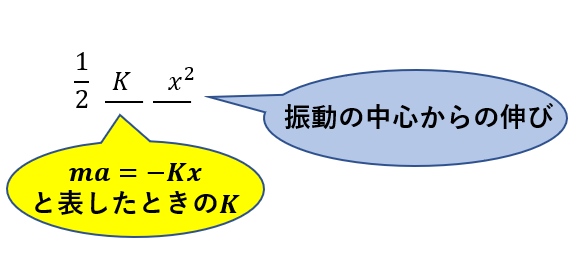
先ほどは鉛直バネ振り子だったので運動方程式を立てると
\(ma = -k(x – \frac{mg}{k})\)
となり、\(K = k\)となりました。なのでばね定数を使うように誤解しがちです。
運動方程式を立てた際に\(K\)に当たるものを使ってください。
単振動のエネルギーを問題での使い方

ただ、問題で使う際にはもっとミスの少ない、簡単な考え方を用いると良いです。
それは水平バネ振り子への置き換えです。
先ほどと同じ鉛直バネ振り子を考えます。

ここで運動合力を求めてみます。
この物体に働く合力を求めます(過程は省略)
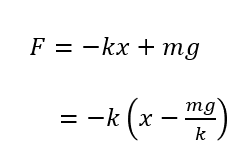
これを先ほどの水平バネの場合と比較してみます。

形がそっくりですよね。
つまり、鉛直バネ振り子は水平バネに置き換えることができます。性質を変えずにうまく置き換えます。
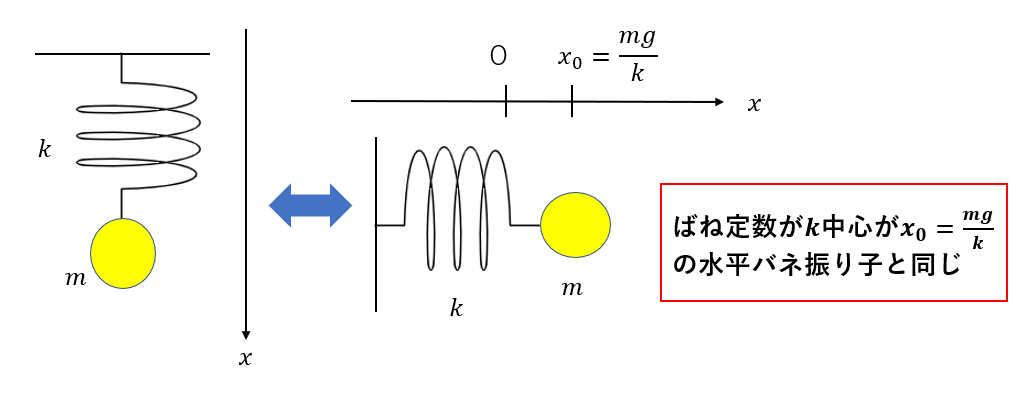
図のように、鉛直バネ振り子は「ばね定数が\(k\)、自然長が\(x_0=\frac{mg}{k}\)の水平バネ」による単振動に置き換えることができるのです。
水平バネ振り子なら「水平」なのでばね重力の位置エネルギーは考えなくてよいというもの直感でわかりますね。
ただし、見ての通り水平バネに置き換えた場合は「\(x_0\)の位置が自然長になる」のでこの位置からの伸びを考える必要があります。
これも先ほど求めたものと一致してますね。
水平バネ振り子にして考えればミスも減って考えやすくなります。
ちなみにこれはエネルギーを考えるだけでなくても使えることなので、困ったときは置き換えをしてみてください。
まとめ:単振動のエネルギー
いかがでしたか?
結論は、最後の置き換えのやり方をマスターしてもらえば大丈夫です。
こちらの方がシンプルで分かりやすいし、問題にも使いやすいので。
ぜひ、この考え方を復習して問題を解いてみましょう!!
単振動のエネルギー保存則
→水平バネに置き換えよ!
・合力を求めて\(F=-k(x-x_0)\)の\(k\)にあたる部分を水平バネのばね定数にする
・\(F = -k(x-x_0)\)の\(x_0\)を水平バネの自然長にする。










