第一宇宙速度と第二宇宙速度とは?万有引力で知っておきたい関係式。

今日は重力について学んでいくよ!!
 AKINORI
AKINORI
え?重力なんてわかってますよ。地球に引っ張られる力ですよね?
 AI
AI
それはそうなんだけど、万有引力から考えて見てみます。
 AKINORI
AKINORI
万有引力というのは
二物体同士が引き合う力
でしたね。
万有引力についてはこちらです。
そして、万有引力をやるうえで知っておいてほしい関係式があります。
それを学んで、第一宇宙速度と第二宇宙速度を考えていきましょう!!
重力と万有引力の関係を表す関係式

ここが一番大事です。
重力と万有引力の関係を導いてみましょう!!
そもそも重力の正体って何かというと
万有引力です。
ですから、重力と万有引力は当然何らかの関係があるはずですよね。
それを式に表してみましょう!!
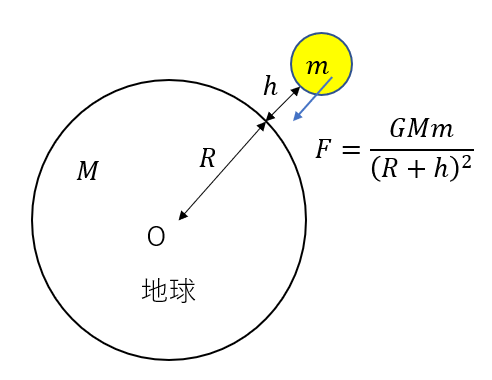
半径\(R\),質量\(M\)の地球があります。
地球の表面から高さ\(h\)の位置に、質量が\(m\)の物体があるとすると、この物体は万有引力を受けますね。
向きは地球の中心向きで
大きさは
\(F = \frac{GMm}{(R + h)^2}\)
です。
さて、僕らの生活は地球の表面付近で行われていますね。
つまり、\(h\)はかなり小さい値です。
また、地球の半径\(R\)はとてつもなく大きいです。
ということは
\(R + h\)は\(R\)と考えても良いですよね?
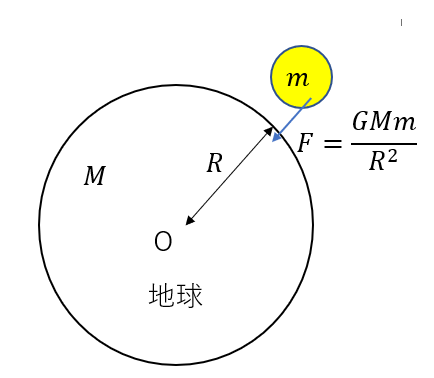
ということで、万有引力の大きさを改めて見てみると
\(F = \frac{GMm}{R^2}\)
特に
\(\frac{GM}{R^2}\)
は一定です。また、これは\(G,M,R\)という地球に固有な値です。
これを改めて
\(\frac{GM}{R^2} = g\)
と置き換えれば
\(F = mg\)
となります。
あ!重力になりました!
 AI
AI
このように、重力は
「地球(惑星)の表面付近での万有引力」
ということなんですね。
また、\(g\)というのは地球(惑星)に固有の定数です。
つまり、地球(惑星)に関してなら、その表面付近ではどこも同じ値をとるわけですよね。
日本、アメリカ、オーストラリア、北極・・・
どこでもこの値は同じです。
地球ではこれがおなじみの\(g = 9.8\)m/s2ですね。
ここまでは理論的なお話です。
重要なのは\(g\)に置き換えた式です。
\(\frac{GM}{R^2} = g\)
∴\(GM = gR^2\)
この関係がパッと出るようにしておいてください。
これはもちろん覚えるべき関係式ではないです。
今やった話を自分で考えて導出できるものです。
ので、自分で導出することができるようにしてください。
〇〇宇宙速度は導出せよ
では、ここから第一宇宙速度と第二宇宙速度というのを見ていきます。
これは必ず導出できるようにしてください。
結果だけを覚えてもしょうがないです。
やることは基本的なことばかりで、
・円運動
・運動方程式
・エネルギー保存
などが分かっていれば簡単に導けます。
第一宇宙速度は円運動

まずは第一宇宙速度です。
第一宇宙速度というのは
惑星表面を一周できる速さ
のことです。
惑星を一周できる速さは求められそうだよね?
 AKINORI
AKINORI
はい!円運動を考えたらいいんですね!
 AI
AI
というわけで考えていきましょう!
今回、表面付近を考えるので、物体は半径\(R\)の位置にあると考えましょう。
あとは円運動を考えればいいわけです。
円運動についてはこちらです。
運動方程式を立てると
\(m\frac{v^2}{R} = \frac{GMm}{R^2}\)
\(v = \sqrt{\frac{GM}{R}}\)
このままでもいいんですが、もっときれいにしたい。
そこで、最初にやったあの関係式を使いましょう。
\(GM = gR^2\)
です。
これを使うと
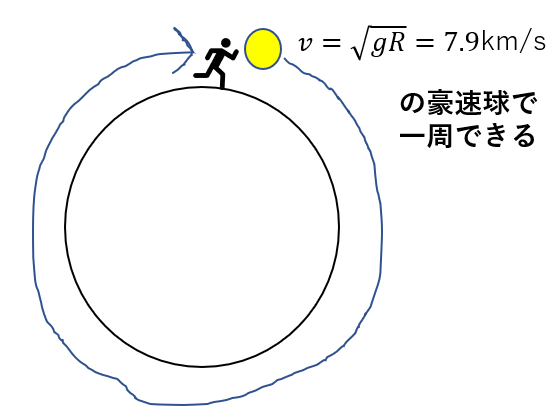
\(v = \sqrt{gR}\)
と書けますね。
これが円運動する速さ、つまり第一宇宙速度ですね。
地球では、この値はだいたい\(7.9\)km/sらしいです。
ですから、アニメや漫画のように、物体を投げて地球を一周させるには
1秒で約8km進むくらいの豪速球を投げる
必要があるわけですね(笑)。
第二宇宙速度はエネルギー保存

続いては第二宇宙速度です。
万有引力は常に引き合う力ですので、地球近くにある物体は地球に引かれるわけです。
地面からジャンプしても、孫悟空やベジータのように空高く飛べず、すぐに地面に戻ってしまいます。
でも、孫悟空やベジータのように勢いよく飛べれば地球から脱出できるのでは??
この地球に引き返されることなく地球から脱出できる速さ
これが第二宇宙速度速度です。
万有引力の大きさは
\(F = \frac{GMm}{r^2}\)
ですよね。
これが働くうちは、地球に戻されるわけです。
じゃあ、どこまで行ったら力がはたらかなくなるのかな?
 AKINORI
AKINORI
ずっと遠く・・・無限遠ですね。あ!無限遠といえば、エネルギーですよね?
 AI
AI
ということで、エネルギー保存を考えてみましょう。
エネルギー保存についてはこちら!!
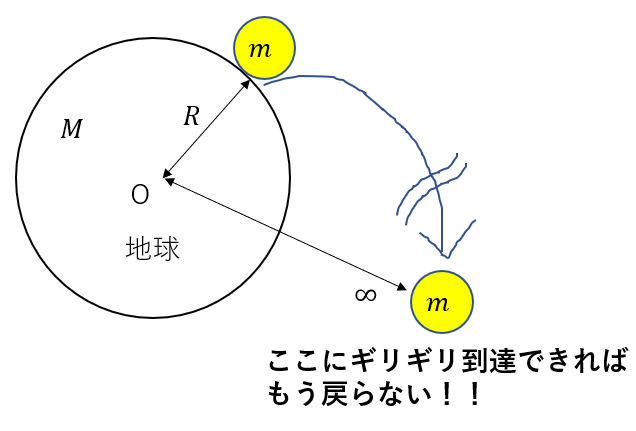
このように、無限遠にギリギリ到達できれば地球に引っ張られることがないので、戻されることはないですね。
そして、万有引力は保存力です。重力が保存力ですから、万有引力も保存力ですよ。
そしてエネルギー保存を考えて見ると・・・
(はじめの力学的エネルギー)+(非保存力にされた仕事)
=(あとの力学的エネルギー)
ですね。
これに当てはめてやればいいんです。
- はじめの力学的エネルギー
速さが\(v\)とすれば
運動エネルギーと万有引力による位置エネルギーを足せばいいので
\(\frac{1}{2}mv^2 + (-\frac{GMm}{R})\)
ですね。
なぜマイナスが付くのか?
これについてはこちらを確認してくださいね。
- 非保存力にされた仕事
今回は、万有引力という保存力のみ働くのでここは0です。
- あとの力学的エネルギー
無限遠なので、万有引力による位置エネルギーは0です。
また、今はギリギリ到達していることを考えているので、無限遠で止まっているのです。
つまり、運動エネルギーも0です。
よって力学的エネルギーも0ですね。
あとは式に当てはめれば良いので・・・
\(\frac{1}{2}mv^2 -\frac{GMm}{R} = 0\)
つまり
\(v = \sqrt{\frac{2GM}{R}}\)
ですね。
もちろんこのままでもいいんですが、さっきと同様
\(GM = gR^2\)
を使ってみると
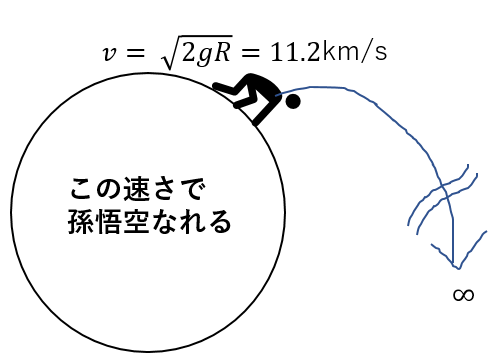
\(v = \sqrt{2gR}\)
はい。これが第二宇宙速度です。
これは地球ではだいたい11.2km/sらしいです。
つまり、
1秒で約11km進むくらいの勢いで地面を蹴れば地球から飛び出せる
ということですね(笑)。
まとめ
ということで、今回やったのは3つです。
- 重力と万有引力の関係\(GM = gR^2\)
- 第一宇宙速度→円運動\((v = \sqrt{gR})\)
- 第二宇宙速度→エネルギー保存\((v = \sqrt{2gR})\)
どれも覚えるのではなく、いつでも導出できるようにしてください。
特に、第一宇宙速度や第二宇宙速度の円運動やエネルギー保存の考え方は、万有引力のどんな問題でも間違いなく使うので、それらを使いこなせるようにしておいてください!!









