ヤングの実験を完全理解!白色光や干渉縞など問題のすべてを教えます

どうも!オンライン物理塾長あっきーです
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
ヤングの実験っていろいろパターンがあって難しいです。どう対策したらいいですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
波動・光の分野で圧倒的に頻出なのが「光の干渉」です。
その中でも「ヤングの実験」は超頻出です。
学校ではいきなりヤングの実験が出てきて、意味も分からずただ問題として解いてしまう高校生も多いかと思いますが、
ヤングの実験はまず歴史的な意味を踏まえたうえで、実際にどんな問題が出るかを把握した方が絶対に良いです。
白色光のときは?
干渉縞がどのように現れるの?
スリットを動かしたらどうなるの?など
ヤングの実験で問われることは決まっています!
この記事では、ヤングの実験の背景と干渉条件の求め方を分かりやすく解説していきます。
最後まで読むことで、入試レベルのヤングの実験の問題が解けるようになります。
・ヤングの実験の意義が分かる
・ヤングの実験の問題が解ける
・白色光の問題が解ける
・干渉縞について説明できる
目次
ヤングの実験って何?
昔は光というのがどんな性質があるのかよく分かっていませんでした。特にこんな論争がありました。
「光って波なの?粒子の??」
実は光の性質をいろいろ調べていると、波のような性質も粒子のような性質も両方あって当時は物理学者を悩ませていました。ですが、どちらも確定的な性質じゃなかったので、何とも言えなかったわけです。
そこで登場したのが、「光は波である」派のヤングさんです。
ヤングさんはこう考えました
「光が波であるなら、干渉という現象が起こるはずだ!」
波であれば山同士、谷同士が重なり合えば波が大きくなって、山と谷が重なり合えば波が小さくなります。
「光でも同じようなことが起きる。光ならたぶん、明るくなったり暗くなったりするはずだ!」
そのように考えたヤングさんは「光の経路差」を変えることで光がどのように見えるかを実験したのです。
それが「ヤングの実験」です。この結果、「光は波の性質を持つ」というのが証明されたのです。
なるほど!そういう背景があるですね。
 AI
AI
それを踏まえてヤングの実験の問題を解いていきましょう!
 AKINORI
AKINORI
ヤングの実験
点Qから波長\(\lambda\)の単色光をスリットS0をもつスリット板W0に照射する。スリットS0によって回折した光はスリットS1, S2によって回折し、スクリーンS上で干渉する。スリットS0はスリットS1, S2と等距離にあるとし、S1S2 = d、スリット板W1とSの距離を\(L\)とする。この時、スクリーン上に現れる明線と暗線の位置について考えよ。なお\(L\)は\(d\)比べ十分に大きいものとする。
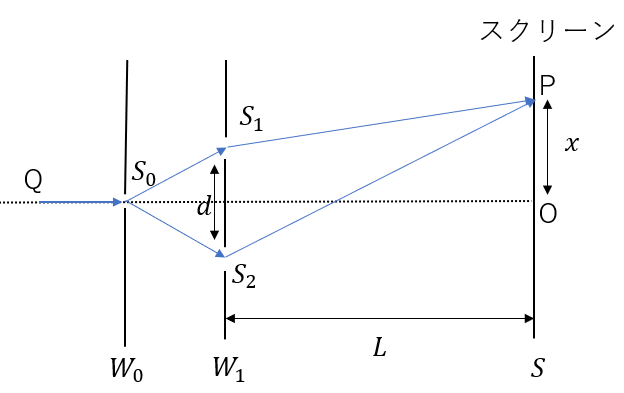
最初のスリットの意味は?
あの、最初にスリット\(S_0\)に照射しなくても良くないですか?
 リケジョ志望のAIさん
リケジョ志望のAIさん
確かにそう思うね。実はこの最初のスリットは重要な役割を果たしているんだ。
 オンライン物理塾長あっきー
オンライン物理塾長あっきー
ヤングの実験では最初にスリットに光を通していますね。
スリットに通さなくても直接2つのスリットに光を照射させてもいいと思いますよね。
しかし最初のスリットがないといけないのです。
でないと、スクリーンに干渉縞が現れなくなるからです。
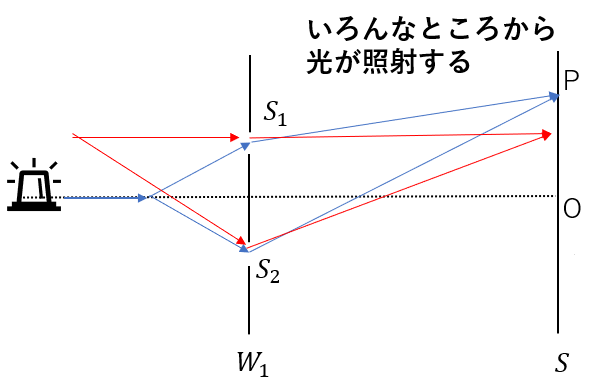
光源から出る光は基本的に四方八方に飛び交います。
ですから、図のように中心から入射する光もあれば、少し上から入射する光もあります。
すると、スクリーンのあらゆる点で明るい点が見ててしまい、光の明暗が区別できなくなります。
光が干渉するかどうかを調べたいのに、明暗がはっきりしていては意味がありません。
ですから、最初のスリットによって中心線から光を解説させることで干渉縞をはっきりさせるのです。
干渉条件を使うので経路差を求める
では、本題に入ります。
どの位置で明線(暗線)が現れるか?
これを考えていきましょう。
干渉条件ということは「経路差」を考えるんですね!
 AI
AI
その通り!いいね~
 AKINORI
AKINORI
今回\(S_0S_1 = S_0S_2\)なので、ここでの経路差は0です。
なので、経路差は図の\(S_1P\)と\(S_2P\)の差を考えれば良さそうですね。
\(S_1\)から次のように垂線\(S_1H\)を引くと、
\(経路差 = S_2 H\)
となります。
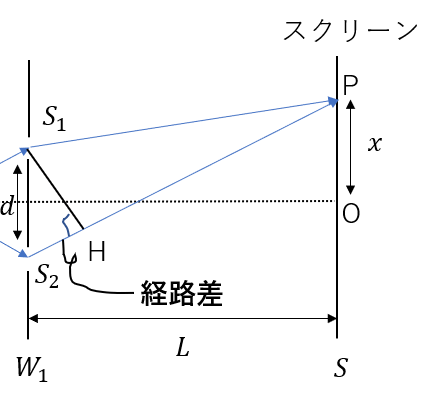
え?なんで、\(S_2H\)が経路差なんですか?\(S_1P\)と\(HP\)の長さって等しくないですよね?
 AI
AI
ここは近似を使ってるよ。この二つの光は平行とみなしていいんだ。
 AKINORI
AKINORI
今回\(L\)が\(d\)より十分に大きいといっています。
実際、この実験は
\(d\)は数ミリメートルですが、\(L\)は数十メートルです。
それを図に表してみると・・・

ということで、二つの光は平行に見ることができます。
平行に見れば、垂線を引いたときに\(S_1P = HP\)とみなせますね。
話を戻して、経路差\(S_2H\)を具体的に求めていきたいと思います。
図のように、\(S_1 S_2\)の中点MからPに向かう角度を\(\theta\)とします。
すると、光やPMが平行ということから、
\(\angle S_2 S_1 H = \theta\)
と表せます。
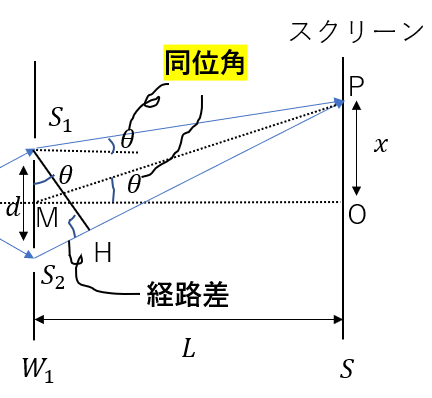
△\(S_1 S_2H\)
に注目して
\(S_2 H = d\sin{\theta}\)
と書けますね。
ここから、さらに近似を使います。
Lがdより十分に大きいということは
\(\theta\)が十分に小さいということです。
この時、
\(\sin{\theta} = \tan{\theta}\)
という近似式が成り立ちます。これは知っておくといろいろ便利です。
\(\tan{\theta}\)は△PMOを見れば良くて
\(\tan{\theta} = \frac{x}{L}\)
です。
なので、経路差を改めて書き直すと・・・
\(経路差=d\frac{x}{L}\)
と書けますね。
光の場合は光路差というものを考えないといけません。それについては別の記事で紹介していますのでそちらを確認ください。
 AKINORI
AKINORI
ということで、干渉条件は
明線・・・\(\frac{dx}{L} = 2m・\frac{\lambda}{2}\)
暗線・・・\(\frac{dx}{L} = (2m + 1)・\frac{\lambda}{2}\)
この干渉条件の出し方についてはこちらの記事で確認ください。
これを\(x\)について考えれば、
スクリーン上に現れる干渉縞がわかりますね。
明線の条件に\(x = 0\)を代入したら\(m = 0\)が解になります。
暗線の条件に\(x = 0\)を代入したら\(m = -\frac{1}{2}\)ですが、これは解になりません。
\(m\)は整数ですので。
つまり、原点では式として成立する明線が現れます。
そこから暗線、明線・・・と交互に現れていく感じですね。
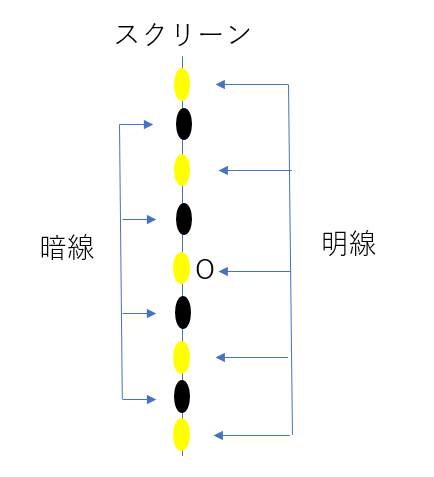
こんな感じのイメージです。
問題で問われるポイント
ヤングの干渉実験で明線と暗線の位置が分かったので、実際に問われるポイントを整理しておくよ!
 AKINORI
AKINORI
その1 明線(暗線)の間隔
まずは、明線(暗線)の間隔です。
これは\(m\)番目と、\(m + 1\)番目の差を考えます。
明線と暗線の条件式を「\(x = \)」の形にした式にして\(m + 1\)のときの式から\(m\)の式を引けばOKです。
- 明線
\(\Delta x = \frac{(m + 1)L\lambda}{d} – \frac{mL\lambda}{d}\)
∴\(\Delta x = \frac{L\lambda}{d}\)
- 暗線
\(\Delta x = \frac{(2m + 3)L\lambda}{d} – \frac{(2m +1)L\lambda}{d}\)
∴\(\Delta x = \frac{L\lambda}{d}\)
どっちも等間隔に並んでいますね!
 AI
AI
その通り!
 AKINORI
AKINORI
というわけで、それぞれ
\(\Delta x = \frac{L\lambda}{d}\)
の間隔で交互に並ぶことがわかりますね。
白色光を照射すると?
この例では「単色光」と言って、色が一つの光だけを考えていました。
でも、身の回りにある光源は「白色光」と呼ばれるいろんな色の光を含んだ光です。
この白色光を使うと明線がどう見えるか?
というのを考えてみたいと思います。
光の色は
波長で決まっています。

青が短く、赤が長い
こういうイメージを持っておいてください。
さて、明線の条件をもう一度見てみましょう。
\(x = \frac{mL}{d}\lambda\)
ある\(m\)について(例えば\(m = 1\))考えると、明線はどう見えるでしょう?
そっか!明線の位置は波長で決まるから、\(\lambda\)の小さい紫が一番原点に近い方に現れるんですね!
 AI
AI
いいね!よく気づきました!
 AKINORI
AKINORI
式を見ればわかりますね。
\(\lambda\)が小さい→\(x\)も小さい
\(\lambda\)が大きい→\(x\)も大きい。
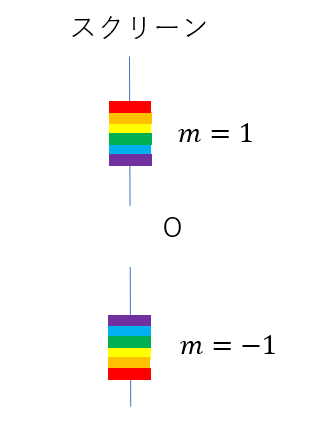
このように
- 原点に近い→紫
- 原点に遠い→赤
という風に現れます。
ただし原点にはすべての波長の光が集まるので、白色に見えます。
この干渉条件を使うときの経路差はいつでも出せるようにしておいてね!
 AKINORI
AKINORI
スリットを動かしたりガラスを挟むとどうなる?
これは完全に入試レベルの問題になります。
よくあるのが、次の二つです。
・片方のスリットの前にガラスをつけるとどうなるか?
・スリット\(S_0\)を上下に動かすとどんな変化が起こるか?
こちらも干渉条件をしっかり使いこなせれば解ける問題です。
これは別で解説したいと思いますので、こちらを確認ください!
干渉条件を式で理解する訓練を積もう
いかがでしたか?
ヤングの実験に限らず、干渉問題ではとにかく干渉条件を導くことです。
ただ、入試レベルだとこの後が難しくなります。
干渉条件の式を見て
何が言えるのかを説明できるようにならなければいけません。
その式から説明する訓練も問題演習を通じてマスターしておきましょう。
ヤングの実験の干渉条件(覚えるな!)
明線・・・\(\frac{dx}{L} = 2m・\frac{\lambda}{2}\)
暗線・・・\(\frac{dx}{L} = (2m + 1)・\frac{\lambda}{2}\)
ヤングの実験で問われること
・明線(暗線)の間隔
・白色光を照射したときの明線の様子
・スリットを動かしたときの明線の変化
・ガラスを入れたときの明線の変化








Comment
明線、暗線の間隔についてはdx/L=…式を変形してx=に変え、それにm=m+1やmを代入する、で合ってますか?
また、光路差を求めて干渉させるとき、途中から水に浸かっている場合もS1とS2からの光は平行と考えて良いのでしょうか?
はい。合ってます。
本当は平行と考えてはいけません。屈折によって向きが変化しますからね。
しかし、問題で出るときは
・全体が物質で満たされる
・ごく一部が物質で満たされる
のように、平行みなせるような状況に設定されます。
なので、平行と考えても問題ないです。
なるほど、じゃあ屈折率のみを考えて、光の屈折を2本の光について個別に考える必要はないということですね!
そうですね。もし何か特別なことを考える場合は、普通は問題文に書いてあるので大丈夫です。